Учебно-методическое и информационное обеспечение дисциплины

Рекомендуемая литература

Основная:

1. Баврин И.И. Математика для гуманитариев: учебник для студентов учреждений высш. Проф. образования гуманитарных направлений. М.: Изд. центр «Академия», 2011. 320 с.

2. Высшая математика для экономистов / Под ред. Н.Ш. Кремера. М.: ЮНИТИ, 2002. 471 с.

3. Ильин В.А., Куркина А.В. Высшая математика: учеб. М.: Проспект, 2009. 608 с.

4. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М, 1997. 208 с.

5. Красс М.С. Математика для экономических специальностей: Учебник. М.: ИНФРА-М, 1999. 464 с.

6. Пехлецкий И.Д. Математика: Учеб. для студ. образоват. учреждений сред. проф. образования. М.: Издательский центр «Академия», 2003. 304 с.

Дополнительная:

1. Ганичева А.В. Краткий курс математического анализа: Учебное пособие. Тверь, 2002. 117 с.

2. Данчул А.Н., Митини А.И., Сафонова Т.Е., Симонов В.А. Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика. Учебно-методическое пособие / Под ред. А.Н.Данчула. М., 2004. 156 с.

3. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. М.: МГУ им. М.В.Ломоносова, Издательство «ДИС», 1998. 368 с.

4. Кремер Н.Ш. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. Пособие. М.: Издательство Юрайт; ИД Юрайт, 2011. 646 с.

5. Луканкин Г.Л., Луканкин А.Г. Высшая математика для экономистов: курс лекций: учебное пособие для вузов. М.: Издательство «Экзамен», 2006. 285 с.

6. Практикум по математике: пособие для студентов 1 курса / сост. А.Л.Кириллов, В.И.Клоков, С.В.Полянская. Спб.: Изд-во СЗАГС, 2009. 100 с.

7. Сборник задач по высшей математике для экономистов: Учебное пособие/ Под ред. В.И. Ермакова. М.: ИНФРА-М, 2004. 575 с.

8. Щипачёв В.С. Высшая математика. Базовый курс: учебное пособие/ под ред. акад. А.Н. Тихонова. М.: Издательство Юрайт; ИД Юрайт, 2011. 447 с.

Интернет-ресурсы

[1] Архив материалов факультета экономики -

http://econ.hsehelp.ru/index.php?option=com_jdownloads&Itemid=&view=vie

wcategory&catid=25

[2] Электронные книги по экономико-математическим методам и моделям -

http://www.aup.ru/books/i008.htm

[3] Экономико-математические методы и прикладные модели -

http://www.eusi.ru/umk/vzfei_ekonomiko_matematiceskie_metody_i/index.shtml

Материально-техническое обеспечение дисциплины

Наименование технического средства	Количество
Сервер
Компьютеры
Проектор
Сканер

Методические рекомендации по организации изучения дисциплины

Для полноценного усвоения курса математического анализа студент должен, прежде всего, овладеть основными понятиями этой дисциплины. Необходимо усвоить определения и понятия, уметь приводить их точные формулировки, приводить примеры объектов, удовлетворяющих этому определению. Кроме того, необходимо знать круг фактов, связанных с данным понятием. Требуется также знать связи между понятиями, уметь устанавливать соотношения между классами объектов, описываемых различными понятиями. Далее, студент должен освоить доказательства основных утверждений и фактов математического анализа. Часть из этих доказательств целесообразно обсуждать на практических занятиях в форме опроса или докладов.

При заочной форме обучения самостоятельная работа студента является основным видом деятельности, позволяющим хорошо усвоить изучаемый предмет и одним из условий достижения необходимого качества подготовки и профессиональной переподготовки специалистов. Она предполагает самостоятельное изучение студентом рекомендованной учебно-методической литературы, различных справочных материалов, подготовку к лекционным и семинарским занятиям, решение практических задач, решение контрольной работы.

Практические и самостоятельные работы организованы в виде следующих компонент:

1. Изучение теоретического материала.

2. Самостоятельное изучение методов решения задач по данному разделу с использованием рекомендованной литературы.

3. Решение задач на и практических занятиях.

4. Выполнение контрольных работ.

Методические рекомендации по организации самостоятельной
работы студентов

Компонентами самостоятельной работы являются:

1. Самостоятельная работа с литературой.

2. Подготовка к практическим занятиям.

3. Подготовка к выполнению аудиторных контрольных работ.

4. Выполнение домашних контрольных работ.

5. Подготовка к экзамену.

Промежуточным контролем знаний студентов в течение обучения являются устные и письменные опросы, контрольные работы, тесты по ключевым темам читаемой дисциплины.

1. Решение задач с использованием методов математического анализа. Примеры задач даны в методическом обеспечении к рабочей программе.

2. Составление опорного конспекта. Пример задания: составьте опорный конспект на одну страницу формата А4 по теме «Производная функции одной переменной».

3. Составление тематического плана. Пример задания: Составьте тематический план, состоящий из 10-12 безглагольных предложения (3-4 слова в каждом), по теме: «Первообразная функция функции действительного переменного».

4. Тестирование. Пример теста.

Предлагается выбрать верный вариант ответа:

Понятие функции

1. Пусть X, Y – числовые множества. Если существует правило f, по которому каждому 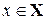ставится в соответствие единственное число 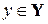, то говорят, что на множестве X задана функция со множеством значений в Y.

2. Пусть X, Y – числовые множества. Если существует правило f, по которому каждому 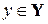ставится в соответствие единственное число 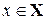, то говорят, что на множестве X задана функция со множеством значений в Y.

3. Пусть X, Y – числовые множества. Если существует правило f, по которому каждому 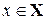ставится в соответствие число 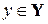, то говорят, что на множестве X задана функция со множеством значений в Y.