Вынужденные колебания

Для того, чтобы колебания не затухали, колебательную систему нужно подпитывать энергией; например, с помощью периодически действующей вынуждающей силы (4.37).

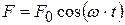. (4.37)

По второму закону Ньютона: 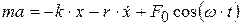; или

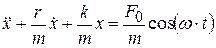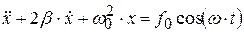, , (4.38)

где 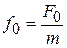. Уравнение (4.38) – дифференциальное уравнение вынужденных колебаний. Его решение (без доказательства):

,

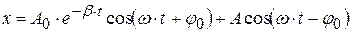причём первое слагаемое при 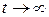затухает и для установившихся колебаний

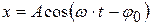. (4.39)

Амплитуда вышужденных колебаний в (4.39) зависит от частоты:

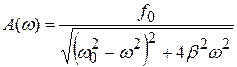(4.40)

Начальная фаза:

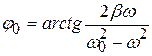. (4.41)

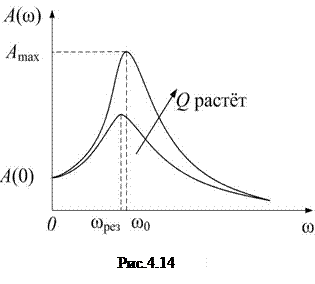
На рис. 4.14 дан график функции (4.40); это – резонансные кривые.

Если 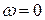, то статическое смещение 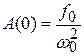. При .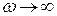

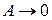Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний системы (резонансной частоте) называется резонансом. Найдём резонансную частоту. Амплитуда максимальна, если подкоренное выражение в знаменателе (4.40) минимально, то есть

;

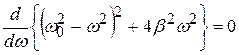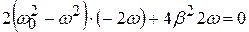; (4.42)

;

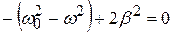откуда

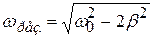. (4.43)

Значение 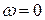– тоже решение уравнения (4.42), но это – минимум. Если же выполняется (4.43), амплитуда вынужденных колебаний максимальна и равна

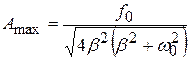. При условии малости затухания ( ):

;

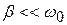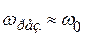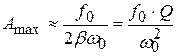. (4.44)

Упругие волны. Основные понятия

Колебания, возбуждаемые в какой-либо точке среды, могут в ней распространяться дальше, так как частицы среды взаимодействуют друг с другом.

Определение: волна – это процесс распространения колебаний, периодический во времени и пространстве.

Природа волн может быть различной (упругие, электрические, электромагнитные…), но закономерности волновых процессов, физически различных, математически описываются одинаково.

В продольной волне колебания происходят параллельно направлению распространения волны; в поперечной – перпендикулярно. При распространении продольной упругой волны происходит деформация сжатия-растяжения; поперечной – сдвига. Деформация сдвига вызывает возникновение упругих сил только в твёрдых телах поперечные волны возможны только в твёрдых телах; а продольные – и в твёрдых, и в жидких, и в газах.

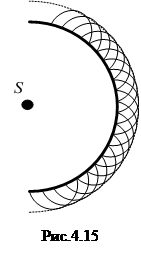Волновой фронт – совокупность точек, до которых дошла волна в данный момент времени. Волновой фронт может быть сферический, плоский. Луч – направление распространения волны. В изотропной среде луч перпендикулярен волновому фронту.

Принцип Гюйгенса (объясняет процесс распространения волн): любая точка волнового фронта является точечным источником вторичных сферических волн.

При распространении упругих волн в среде любая частица колеблется около своего положения равновесия. Переноса частиц среды не происходит. Волной переносится энергия. Все частицы колеблются с одинаковой частотой, определяемой частотой источника.

Колебания любой новой частицы, захваченной волновым процессом, отстают по фазе от колебаний предыдущей частицы. Скорость перемещения фиксированной фазы называется фазовой скоростью .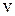

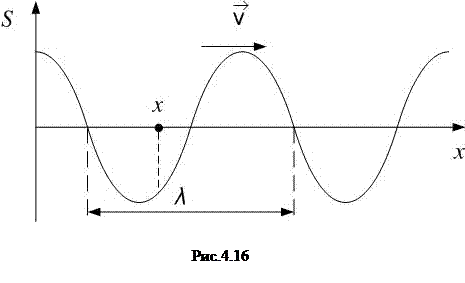
Пусть в точке с координатой 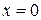(рис.4.16) величина 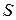колеблется по закону:

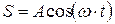. (4.45)

Для любой другой точки с координатой x запаздывание по фазе будет определяться временем запаздывания (в течение этого времени волна дойдёт до точки x):

.

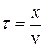Заменив в (4.45) переменную 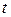на 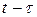, получим уравнение плоской волны для точки x:

;

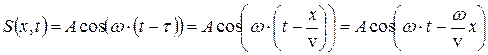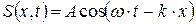, (4.46)

где 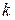– волновой вектор (волновое число):

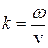. (4.47)

Определение: длина волны 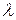– это расстояние, на которое распространяется волна за время, равное периоду:

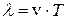. (4.48)

Или: 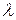– это минимальное расстояние между двумя точками, которые колеблются в одинаковой фазе (рис.4.16).

Из (4.47) и (4.48):

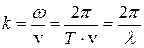. (4.49)

Поскольку фаза 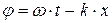, то 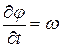- характеризует быстроту изменения фазы во времени; 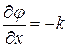- характеризует быстроту изменения фазы в пространстве.

Найдём скорость перемещения постоянной фазы (фазовую скорость); для этого положим

,

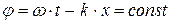тогда

,

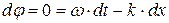откуда

.
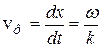