Метод искусственного базиса

Метод искусственного базиса применяется для решения задач линейного программирования в случае, когда задача не имеет начального опорного решения с базисом из единичных векторов.

Согласно данному методу для задачи линейного программирования составляется так называемая расширеннаязадача, которая решается симплексным методом. На основе результатов решения расширенной задачи либо находится оптимальное решение исходной задачи, либо устанавливается причина его отсутствия.

Пусть имеется каноническая задача линейного программирования:

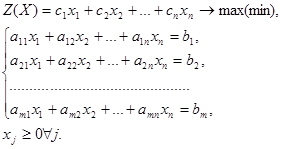(3.1)

Без ограничения общности можно считать, что правые части уравнений системы ограничений неотрицательны, т.е.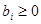

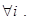
В дальнейшем для краткости записи при доказательствах используется компактная запись этой задачи:

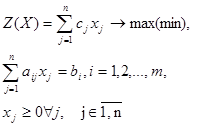
(3.2)

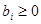
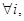
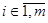
Для исходной задачи составляется расширенная задача. При этом используется искусственные переменные.

Искусственными переменныминазываются неотрицательные переменные, которые вводятся в ограничения-равенства для получения начального опорного решения с базисом из единичных векторов. Каждая искусственная переменная вводится в левую одного из уравнений системы ограничений с коэффициентом +1 и в целевую функцию в задаче на максимум с коэффициентом –M, а в задаче на минимум с коэффициентом +M. Число M сколь угодно большое по сравнению с единицей (M>>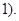

В общем случае расширенная задача на максимум имеет вид:

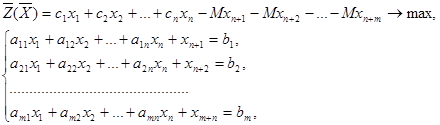
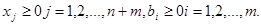(3.3)

или в компактной записи:

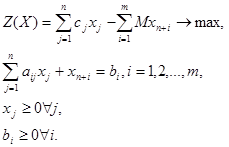(3.4)

Данная задача имеет начальное опорное решение 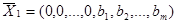с базисом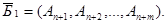

Здесь и в дальнейшем для расширенной задачи отмечаются чертой сверху следующие величины: целевая функция 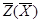, допустимое решение 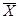, опорные решения 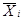, базисы опорных решений 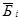, область допустимых решений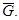

Для обоснования метода используются две леммы и три теоремы.

Лемма 3.1.Любому допустимому решению 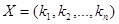исходной задачи программирования соответствует допустимое решение расширенной задачи 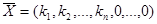и, наоборот, любому допустимому решению расширенной задачи 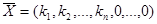соответствует допустимое решение исходной задачи 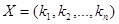. При этом значение целевых функций задач на соответствующих решениях совпадают, т.е. .

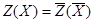Лемма 3.2.Значение целевой функции расширенной задачи на максимум (минимум) на любом допустимом решении 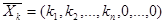,у которого все искусственные переменные равны нулю, больше (меньше) значения целевой функции на любом допустимом решении 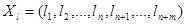, у которого хотя бы одна искусственная переменная отлична нуля.

Теорема 3.2.(признак оптимальности решения). Если расширенная задача линейного программирования имеет оптимальное решение 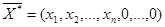, у которого все искусственные переменные равны нулю, то исходная задача имеет оптимальное решение 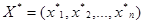, которое получается из 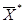отбрасыванием этих нулевых искусственных переменных.

Теорема 3.3.(признак отсутствия решения ввиду несовместности системы ограничений). Если расширенная задача имеет оптимальное решение, у которого хотя бы одна искусственная переменная отлична от нуля, то исходная задача не имеет решения ввиду несовместности системы ограничений.

Теорема 3.4. (признак отсутствия решения ввиду неограниченности целевой функции). Если расширенная задача не имеет решения ввиду неограниченности целевой функции, то исходная задача также не имеет решения по той же причине.