Бинноминальный закон распределения случайной величины

ОПР: законом распределения случайной величины наз соот-ие между значениями случ-й величины и их верот-ми.

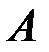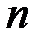Теорема. Математическое ожидание числа появлений события в независимых испытаниях равно произведению числа испытаний на вероятность появления события 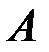в каждом испытании.

Теорема. Дисперсия числа появлений события 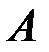в 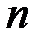независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события 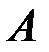в одном испытании: .

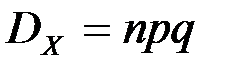Биномиальный закон распределения часть приходится применять в условиях, когда число независимых испытаний велико. Вычисление вероятностей по формуле Бернулли при этом усложняется, поэтому представляет интерес асимптотическое приближение для биномиального закона, справедливое при больших 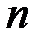. Возможны два случая:

1. Когда при увеличении числа испытаний математическое ожидание рассматриваемой случайной величины 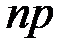тоже неограниченно возрастает (случай постоянного 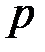); при этом биномиальное распределение сходится к нормальному закону, который будет рассмотрен позже.

2. Когда при увеличении числа испытаний остается постоянным произведение 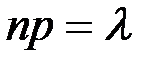, то есть математическое ожидание рассматриваемой случайной величины остается конечным. Это означает, что вероятность события 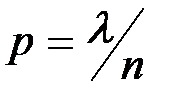стремится к нулю. В этом случае биномиальное распределение сходится к распределению Пуассона.

РАСПРЕДЕЛЕНИЕ ПУАСОНА СЛУЧАЙНОЙ ВЕЛИЧИНЫ

ОПР:Случайная величина 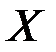называется распределенной по закону Пуассона с параметром 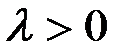, если эта случайная величина может принимать значения 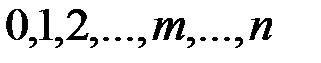, соответствующая вероятность которых определяется по формуле Пуассона, когда :

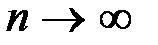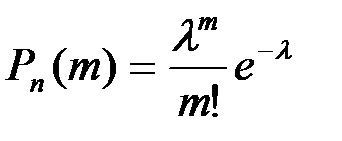
ТЕОРЕМА: М случ величины распред-ой по закону Пуассона =λ Д=λ, ϭ(х)=

Нормальное распределение

ОПР: Нормальным называется такое распределение случайной величины 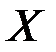, плотность вероятности которого описывается функцией Гаусса:

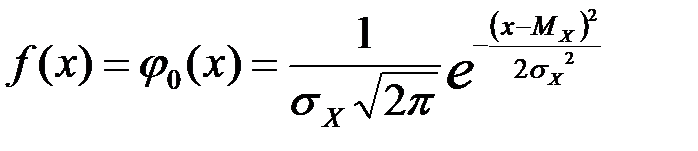
где 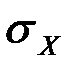– среднее квадратичное отклонение;

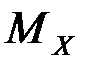– математическое ожидание случайной величины.

ТЕОРЕМА: М(х)=m D(x)=ϭ ϭ(x)=ϭ

21. ОПР: Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:

,

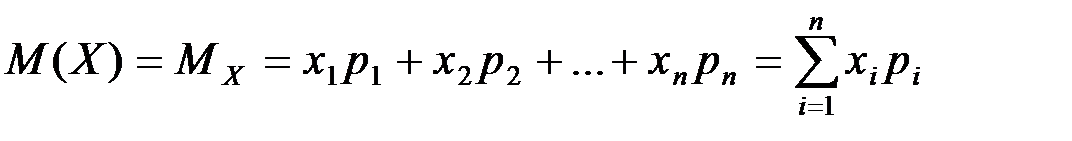где .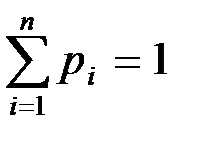

Свойства математического ожидания

1. Математическое ожидание постоянной величины 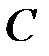равно этой величине.

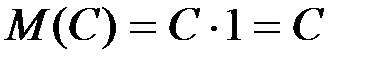
2. M(CX)= C·M(X)

3. M(X+Y)=M(X)+M(Y)

4.

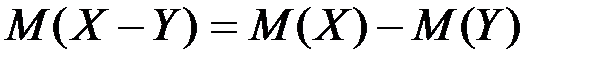
5.

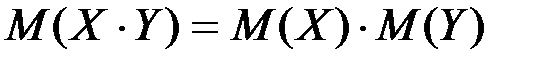
22.ОПР: Дисперсией случайной величины 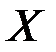называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания:

.

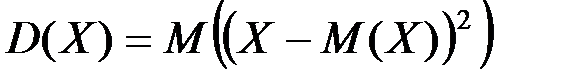Свойства дисперсии

1. Дисперсия постоянной величины равна нулю.

2.

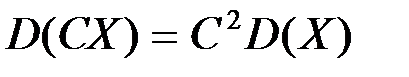
3.

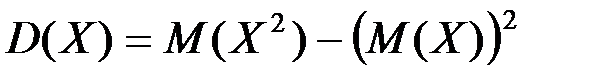
4.

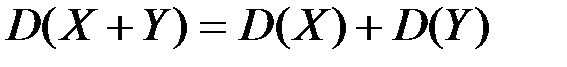
5. D(X-Y)= D(X)-D(Y)