Векторный метод решения задачи Л П
Рассмотрим данный метод, как метод, относящийся к группе методов возможных направлений, оценим его преимущества и недостатки по сравнению с традиционным С М. Проиллюстрируем интерпретацию данного метода решенным ранее примером:
 Min {Z=Sxj}
Min {Z=Sxj}
3 x1 + 2 x2 + 10 x3 ≥ 80
 x1 + 6x2 + x3 + 13 x4 ≥ 40
x1 + 6x2 + x3 + 13 x4 ≥ 40
" xj ≥ 0, j=1,4
В данном случае интерпретацию на плоскости можно дать, если число ограничений в системе не превышают двух. Отложим в системе координат шкалы ограничений.
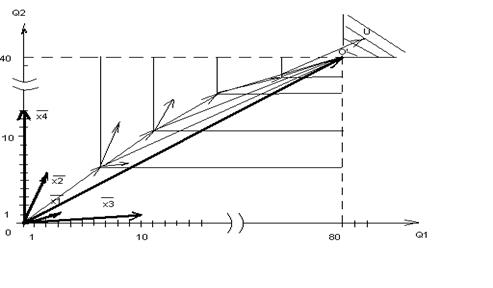
Данные ограничения позволяют задать допустимую область решений U. Естественно так как требуется достигнуть данного ограничения с минимальными потерями (нас интересует оптимальное решение), что обеспечивается кратчайшим путем между точками
О и О’, следует провести вектор ОО’, задающий кратчайший путь к области допустимых решений. Каждое возможное решение, задаваемое системой ограничений, так же можно представить собственным вектором на данной плоскости. В частности, если принять x1 = 1 (х=3, у=1, см. исходную задачу), ему будет соответствовать вектор x1. Соответственно получаем все остальные вектора. Очевидно, что для заданных ограничений лучшим был бы вектор или решение, которое позволяет продвигаться со скоростью 2/1 или совпадающим по направлению с идеальным вектором ОО’. Однако для заданной задачи подобного вектора нет, Þ возникает задача выбора оптимального решения (выбора параметра rk в уравнении (5)).
Так как вектор в общем случае характеризуется 2-мя параметрами (длинной и направлением), в данном случае величиной угла между им и идеальным вектором ОО’, что с определенными оговорками можно свести к одному критерию выбора лучшего вектора по длине его проекции на идеальный вектор ОО’. Итак, по величине длины проекции можно выбрать лучший вектор на данном шаге (в данном случае в качестве ak предполагаем 1 – один отложенный вектор). Отложение выбранного лучшего вектора на данном шаге (что означает присвоение соответствующей переменной xi значения 1) приближает нас к допустимой области решений Þ для перехода к следующему шагу оптимизации, следует перенести начало системы координат в направлении и на величину выбранного лучшего вектора. Соответственно строится и новый идеальный вектор, учитывающий достижение заданных ограничений на предыдущих этапах. В новой системе опять откладываются исходные векторы, и вновь выбирается лучший вектор. Данная процедура выполняется до тех пор, пока последний лучший из отложенных векторов не пересечет допустимую область решений. Совокупность отложенных векторов на всех этапах и определяет оптимальный план или оптимальное решение.
Замечание: видим, что в данном случае мы получаем оптимальное решение целочисленной задачи.
