Решение задач оптимального управления в Excel
Excel позволяет решать задачи оптимального управления, общий вид которых представлен формулами 1-5.
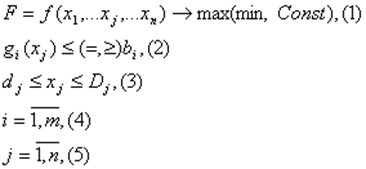
где xj может принимать либо действительные, либо целочисленные, либо булевы значения.
Формула 1 определяет целевую функцию, формула 2 определяет ограничения, а формула 3 определяет граничные условия. В зависимости от вида функции f в формуле 1 задача может относиться либо к классу задач линейного или нелинейного программирования. В зависимости от того, являются ли xj целыми и булевыми или действительными величинами задача может относиться к задачам целочисленного программирования или нет.
Для решения таких задач в Excel предусмотрена надстройка «Поиск решения», которую можно вызвать из меню «Сервис». Если пункта меню «Поиск решения» нет, то нужно вернуться к установке Excel и установить эту надстройку.
Поиск решения (рацион)
Excel имеет несколько программ-надстроек, выполняющих решение различных задач. Одной из надстроек является "Поиск решения", позволяющая решать оптимизационные задачи в Excel. Чаще всего это задачи линейного программирования (ЛП).
Общая формулировка задачи ЛП: найти неотрицательное решение X системы линейных уравнений AX=B, при котором целевая функция f=CX принимает максимальное (минимальное) значение, где A — матрица коэффициентов; B — объемы ресурсов.
Экономический смысл системы AX=B заключается в задании ограничений на расходуемые ресурсы.
Экономический смысл целевой функции f=CX заключается в максимальной прибыли или минимальной себестоимости, получаемой от оптимального решения X. Например, если X — вектор объемов выпуска продукции, а С - вектор прибыли, получаемой от единицы каждого вида продукции, то f — суммарная прибыль от выпуска всей продукции.
Рассмотрим работу надстройки "Поиск решения" на примере задачи о рационе кормления животных. Требуется составить такой рацион кормления животных тремя видами корма, при котором они получат необходимое количество питательных веществ A и B и себестоимость кормов будет минимальна. Цены кормов, требуемое количество питательных веществ и их содержание в каждом корме показаны в таблице.
| Питательные вещества | Корм 1 | Корм 2 | Корм 3 | Требуемое количество (ед. пит. вещества) |
| А (ед./кг) | ||||
| Б (ед./кг) | ||||
| Цена корма (руб/кг) | 2,20 | 1,95 | 2,87 |
Если обозначить X=(x1, x2, x3) — искомое количество кормов, то задача ЛП формулируется так:
Найти решение X системы
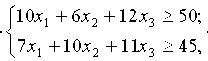
при котором целевая функция
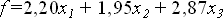
принимает минимальное значение.
Математическую формулировку задачи необходимо оформить в виде таблицы, отражающей основные зависимости.
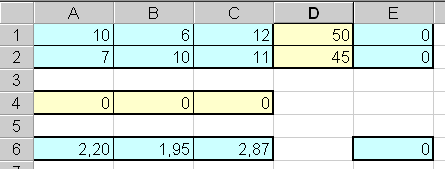
Ячейки таблицы имеют следующий смысл:
- диапазон A1:C2 — содержит матрицу A;
- диапазон D1:D2 — содержит вектор ресурсов В;
- диапазон A6:C6 — содержит вектор цен С;
- диапазон A4:C4 — содержит вектор решений X, начальные значения которого заданы нулю и который будет оптимизирован программой;
- диапазон E1:E2 — содержит выражения, вычисляющие произведение AX;
- ячейка E6 — содержит выражение, вычисляющее f=CX.
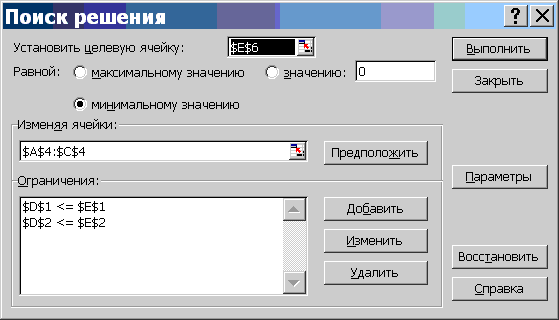
Вызов программы поиска решения выполняется через меню "Сервис\Поиск решения...". В открывшемся окне "Поиск решения" необходимо установить следующие параметры:
- "Установить целевую ячейку" — E6;
- установить переключатель "Равной минимальному значению";
- в поле "изменяя ячейки" указать диапазон A4:C4;
- в области "Ограничения" нажать кнопку "Добавить" и в окне "Добавление ограничений" ввести ограничения: E1>=D1 и E2>=D2;
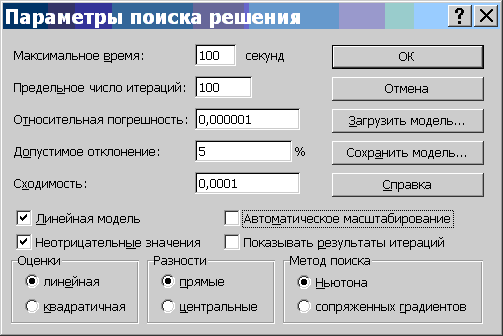
- нажать кнопку "Параметры..." и в открывшемся окне установить флажки "Линейная модель", "Неотрицательные значения" и выбрать переключатель "Оценка" — "Линейная".
Для запуска программы необходимо в окне "Поиск решения" нажать кнопку "Выполнить". Результаты вычислений будут записаны в изменяемые ячейки таблицы. В итоге таблица должна иметь следующий вид.
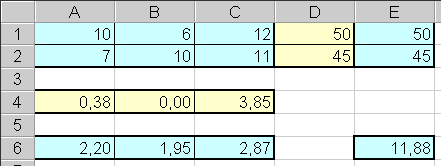
Таким образом, животных следует кормить первым кормом в количестве 0,38 кг, третьим — 3,85 кг и не использовать второй корм вообще. При таком рационе затраты на кормление одного животного составят 11,88 руб.
