Элементы линейной алгебры. Задача 5.Найти матрицу, обратную матрице
Задача 5.Найти матрицу, обратную матрице
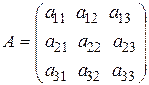 .
.
Проверить результат, вычислив произведение данной и обратной матриц.
5.1. 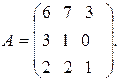 5.2.
5.2. 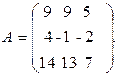 5.3.
5.3. 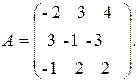
5.4. 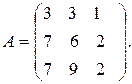 5.5.
5.5. 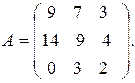 5.6.
5.6. 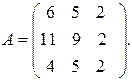
5.7. 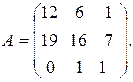 5.8.
5.8. 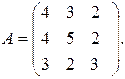 5.9.
5.9. 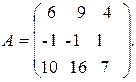
5.10. 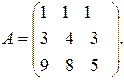
Задача 6. Дана система линейных уравнений

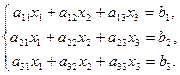
Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:
6.1. 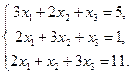
6.2. 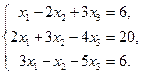
6.3. 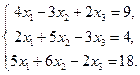
6.4. 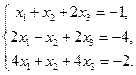
6.5. 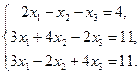
6.6. 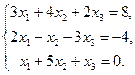
6.7. 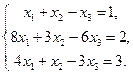
6.8. 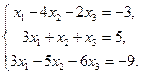
6.9. 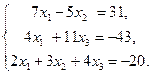
6.10. 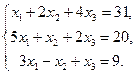
Введение в математический анализ
Задача 7.Найти пределы функций, не пользуясь правилом Лопиталя:
7.1.
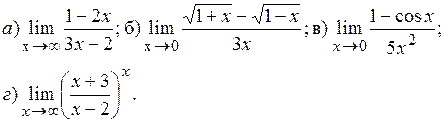
7.2.
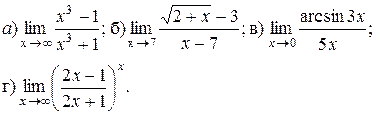
7.3.
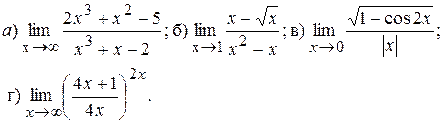
7.4.
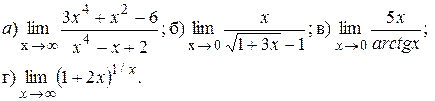
7.5.
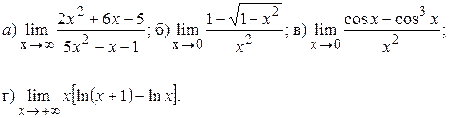
7.6.
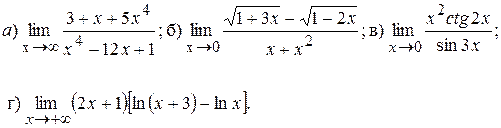
7.7.
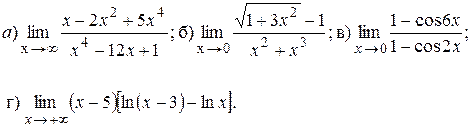
7.8.
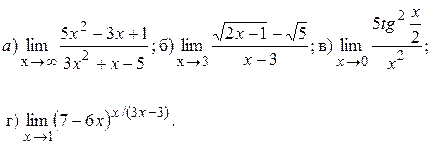
7.9.
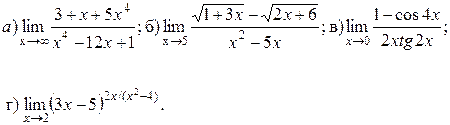
7.10.
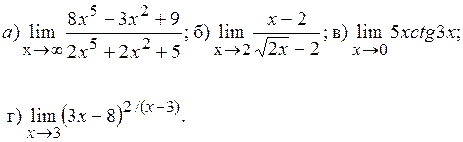
Задача 8. Найти пределы функций, не пользуясь правилом Лопиталя:
8.11)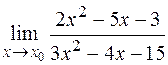 ;при: а)
;при: а) 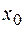 = 2,
= 2,  б)
б) 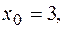
 в)
в) 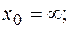
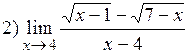 ;
; 
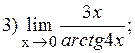
 4)
4) 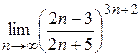 .
.
8.2.1) 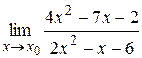 при: а)
при: а) 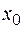 = 0; б)
= 0; б) 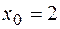 ; в)
; в) 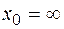 ;
;
2) 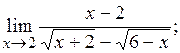
 3)
3) 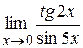 ; 4)
; 4) 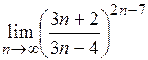 .
.
8.3.1)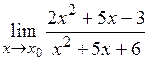 при: а)
при: а) 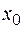 = 3; б)
= 3; б) 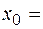 -3 ; в)
-3 ; в) 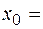
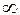 ;
;
2) 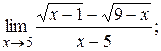 3)
3) 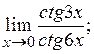 4)
4) 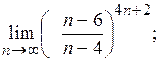
8.4.1) 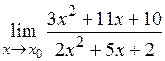 ; при: а)
; при: а) 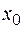 = -3; б)
= -3; б) 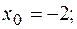 в)
в) 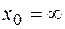 ;
;
2) 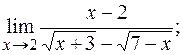 3)
3) 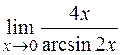 ; 4)
; 4) 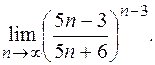
8.5.1) 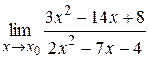 при: а)
при: а) 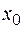 = 2; б)
= 2; б) 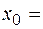 4; в)
4; в) 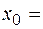
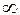 ;
;
2) 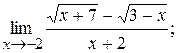 3)
3) 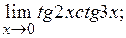 4)
4) 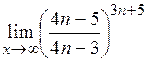 .
.
8.6.
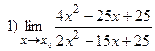 при: а)
при: а) 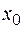 = 2; б)
= 2; б) 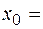 5; в)
5; в) 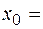
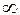 ;
;
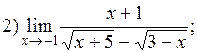 3)
3) 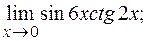 4)
4) 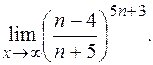
8.7.1) 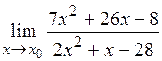 при: а)
при: а) 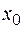 =1; б)
=1; б) 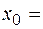 -4; в)
-4; в) 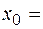
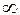 ;
;
2) 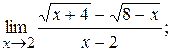 3)
3) 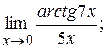 4)
4) 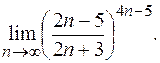
8.8.1) 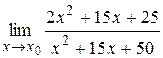 при: а)
при: а) 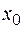 =5; б)
=5; б) 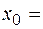 -5; в)
-5; в) 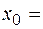
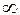 ;
;
2) 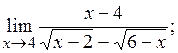 3)
3) 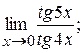 4)
4) 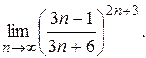
8.9.1) 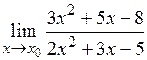 при: а)
при: а) 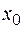 =-2; б)
=-2; б) 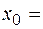 1; в)
1; в) 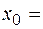
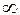 ;
;
2) 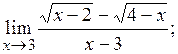 3)
3) 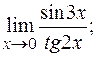 4)
4) 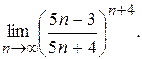
8.10.1) 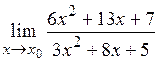 при: а)
при: а) 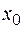 =-2; б)
=-2; б) 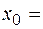 -1; в)
-1; в) 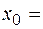
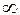 ;
;
2) 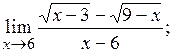 3)
3) 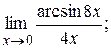 4)
4) 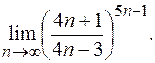
Задача 9.Задана функция у=f(x). Найти точки разрыва функции, если они существуют.
9.1. 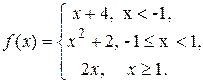 9.2.
9.2. 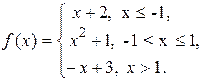
9.3. 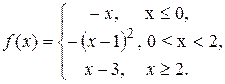 9.4.
9.4. 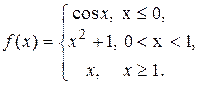
9.5. 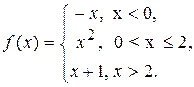 9.6.
9.6. 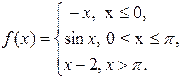
9.7. 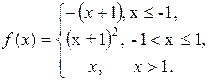 9.8.
9.8. 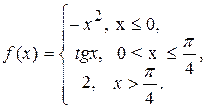
9.9. 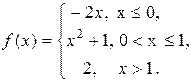 9.10.
9.10. 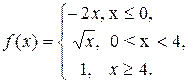
Дифференциальное исчисление функций одной переменной
Задача 10. Найти производные заданных функций.
10.1. 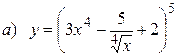 ;
; 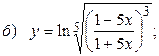
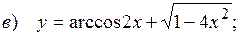
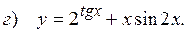
10.2. 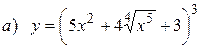 ;
; 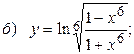
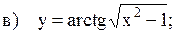
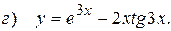
10.3. 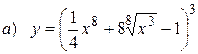 ;
; 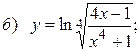
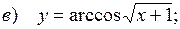
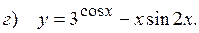
10.4. 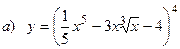 ;
; 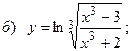
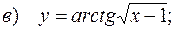
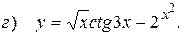
10.5. 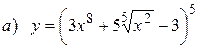 ;
; 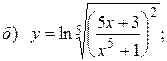
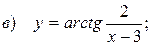
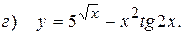
10.6. 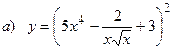 ;
; 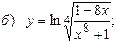
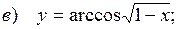
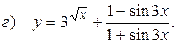
10.7. 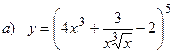 ;
; 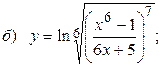
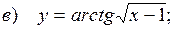
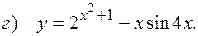
10.8. 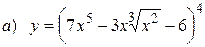 ;
; 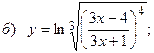
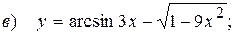
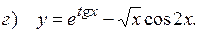
10.9 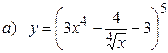 ;
; 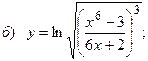
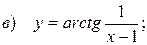
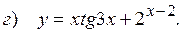
10.10. 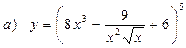 ;
; 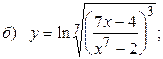
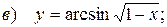
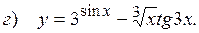
Исследование функций с помощью производных
Задача 11. Исследовать методами дифференциального исчисления функцию у = f(x) и, используя результаты исследования, построить ее график.
11.1. 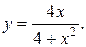 11.2. у =
11.2. у = 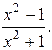 11.3.у =
11.3.у = 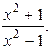
11.4. у = 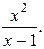 11.5.у =
11.5.у = 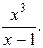 11.6.
11.6. 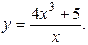
11.7. 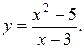 11.8.
11.8. 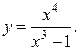
11.9. 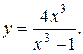 11.10.
11.10. 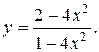
Дифференциальное исчисление функций нескольких переменных
Задача 12.Дана функция 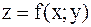 и две точки
и две точки 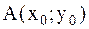 и
и 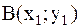 . Требуется: вычислить значение
. Требуется: вычислить значение 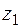 в точке В; 2) вычислить приближенное значение функции
в точке В; 2) вычислить приближенное значение функции 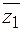 в точке В, исходя из значения
в точке В, исходя из значения 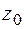 функции в точке А и заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом; 4) составить уравнение касательной плоскости к поверхности
функции в точке А и заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом; 4) составить уравнение касательной плоскости к поверхности 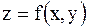 в точке
в точке 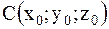 .
.
12.1. 161. 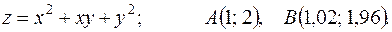
12.2. 162. 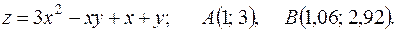
12.3. 163. 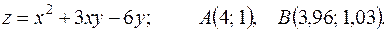
12.4. 164. 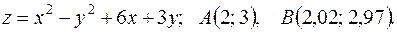
12.5. 165. 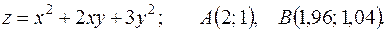
12.6. 166. 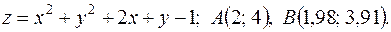
12.7. 167. 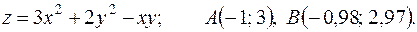
12.8. 168. 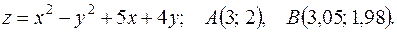
12.9. 169. 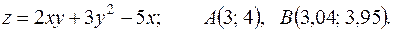
12.10. 170. 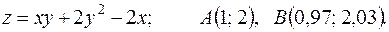
Задача 13. Найти наименьшее и наибольшее значения функции z = f(x; y) в замкнутой области Д, заданной системой неравенств. Сделать чертеж.
13.1. 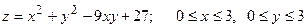 .
.
13.2. 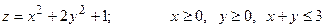 .
.
13.3. 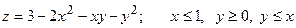 .
.
13.4. 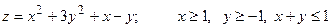 .
.
13.5.  .
.
13.6. 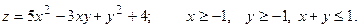
13.7. 
13.8. 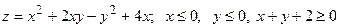 .
.
13.9.  .
.
13.10. 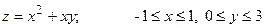 .
.
Задача 14.Даны функция 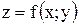 , точка
, точка 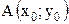 и вектор
и вектор 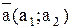 .
.
Найти: 1) 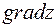 в точке А; 2) производную в точке А по направлению вектора
в точке А; 2) производную в точке А по направлению вектора 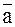 .
.
14.1.  .
.
14.2.  .
.
14.3.  .
.
14.4.  .
.
14.5.  .
.
14.6.  .
.
14.7. 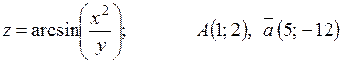 .
.
14.8.  .
.
14.9.  .
.
14.10.  .
.
Задача 15.Экспериментально получены пять значений функции 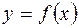 при пяти значениях аргумента, которые записаны в таблице:
при пяти значениях аргумента, которые записаны в таблице:
 | |||||
 |  |  |  |  |  |
Методом наименьших квадратов найти функцию вида 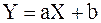 , выражающую приближенно (аппроксимирующую) функцию
, выражающую приближенно (аппроксимирующую) функцию 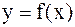 . Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции
. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции 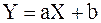 .
.
15.1. 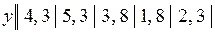
 .
.
15.2. 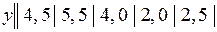 .
.
15.3. 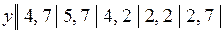 .
.
15.4. 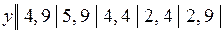 .
.
15.5. 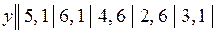 .
.
15.6. 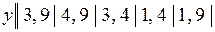 .
.
15.7. 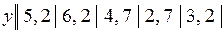 .
.
15.8. 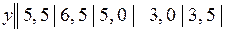 .
.
15.9. 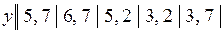 .
.
15.10. 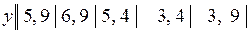 .
.
Задача 16.Найти полный дифференциал функции z =f (x ;y) .
16.1. 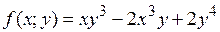 .
.
16.2. 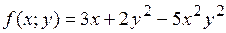 .
.
16.3. 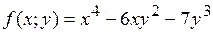 .
.
16.4. 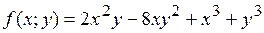 .
.
16.5. 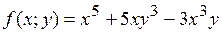 .
.
16.6. 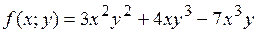 .
.
16.7. 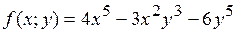 .
.
16.8. 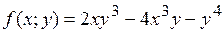 .
.
16.9. 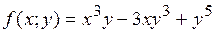 .
.
16.10. 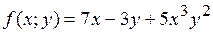 .
.
Неопределенный и определенный интегралы
Задача 17. Найти неопределенные интегралы. Результаты проверить дифференцированием.
17.1. 


17.2. 
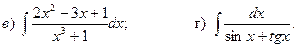
17.3. 
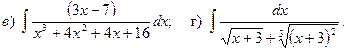
17.4. 
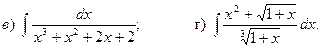
17.5. 
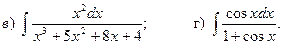
17.6. 

17.7. 

17.8. 

17.9. 

17.10. 

Задача 18. Вычислить площадь фигуры, ограниченной параболой 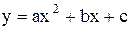 и прямой
и прямой 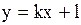 . Сделать чертеж.
. Сделать чертеж.
18.1. 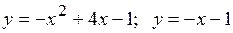 .
.
18.2. 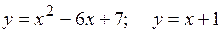 .
.
18.3. 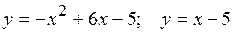 .
.
18.4. 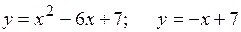 .
.
18.5. 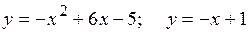 .
.
18.6. 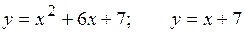 .
.
18.7. 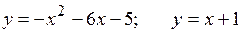 .
.
18.8. 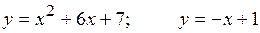 .
.
18.9. 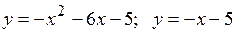 .
.
18.10. 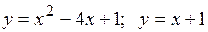 .
.
Задача 19
19.1.Вычислить площадь фигуры, ограниченной параболой 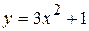 и прямой
и прямой 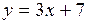 .
.
19.2.Вычислить площадь фигуры, ограниченной одной аркой циклоиды 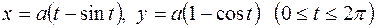 и осью Ох.
и осью Ох.
19.3.Вычислить площадь фигуры, ограниченной кардиоидой 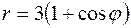
19.4.Вычислить площадь фигуры, ограниченной четырехлепестковой розой 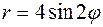 .
.
19.5.Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами 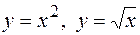 .
.
19.6.Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом 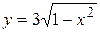 , параболой
, параболой 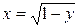 и осью Оу.
и осью Оу.
19.7.Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми 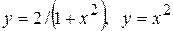 .
.
19.8.Вычислить длину полукубической параболы 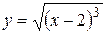 от точки
от точки
А(2;0) до точки В(6;8).
19.9.Вычислить длину кардиоиды 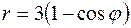 .
.
19.10.Вычислить длину одной арки циклоиды 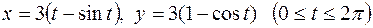 .
.
