Искривленные многообразия (пространства с афинной связностью)

Общая теория описания неоднородностей среды, проявляющихся в аномальном (отличном от соответствующего однородного) поведении поля, развитая в предыдущем разделе может быть конкретизирована в разных аспектах.

Зависимость группы G(s) операторов В, действующих на поле от координат привели к появлению удлиненных производных. Эта зависимость возникла как результат представления на функциях поля группы координстно зависимых координатных преобразований g(s). Но такая зависимость может быть введена и самостоятельно, без связи с координатными преобразованиями. Наконец, элементы группы G(s) могут быть комбинацией первого и второго. Строго говоря, теория, построенная в предыдущем разделе, основана лишь на операторах В(х) из группы G(s) и не требует введения группы g(s) элементов координатных преобразований. Последние, по сути, играли роль лишь для пояснения подхода.

Рассмотрим, как локальное нарушение симметрии может быть введено, например, для векторных полей.

Далее мы используем понятие вектора как многокомпонентного объекта с заданным законом преобразования компонент при координатных преобразованиях.

По порочной традиции зачастую используется псевдонаучный жаргон. Так, используют термин вектор для характеристики любого многокомпонентного объекта. Например, говорят «вектор параметров некоторой физической модели», имея в виду набор параметров, полностью характеризующий этот физический объект (см. приложение 1). При этом не уточняется, какова природа этих параметров и можно ли их, с полным для того основанием, называть вектором. На самом деле, понятие вектора тесно связано с понятием преобразования координат. Вектор – это как раз такой многокомпонентный объект, компоненты которого при координатных преобразованиях преобразуются по заданному конкретному закону. И именно это свойство физических параметров должно давать основания называть их векторами.

Пусть поле 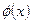представляет собой поле векторов в пространстве 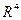с компонентами[48] 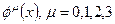. Напомним, что вектор 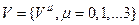при координатных преобразованиях 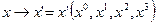«в приказном порядке» изменяется по закону

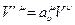, (4.22)

где матрица А, состоящая из элементов 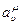, имеет обратную в рассматриваемой области 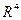и образована элементами:

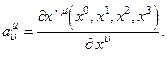(4.23)

Вектора с верхними индексами, преобразующиеся по закону (1) с коэффициентами, вычисляемыми по (14), называются контравариантными векторами. Само же преобразование (14) называется преобразованием по контравариантным индексам.

Могут быть введены вектора с нижними индексами 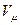, которые также в «приказном порядке» при преобразованиях координат:

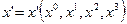
меняются по закону:

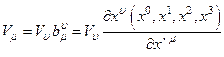. (4.24)

Такие векторы называются ковариантными векторами, а преобразование (15) – преобразованием по ковариантным индексам.

Для более сложных образований – тензоров– многоиндексных объектов, его верхние индексы преобразуются по контравариантному закону, а нижние по ковариантному. Это, по существу, следует воспринимать как определение тензора. При этом порядок, в котором расположены индексы, имеет существенное значение. Так, например, три раза контравариантный и один раз ковариантный тензор 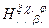преобразуется в 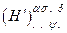по закону: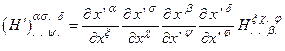

Рассмотрим теперь в качестве преобразования В(х), образующих группу G(s), преобразования векторов по закону (1). Локальное нарушение симметрии, связанное с такими преобразованиями, приводит, в соответствии с (3.6), к удлиненной производной:

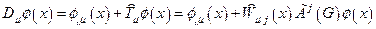(4.25)

Последнее выражение следует переписать в покомпонентной для элементов поля 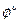форме:

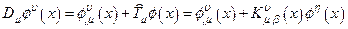, 3

где одним коэффициентом 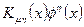обозначена 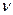- компонента выражения:

.

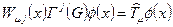Коэффициенты называются афинной связностьюв 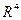или просто связностью. Таким образом, афинная связность представляет собой частный случай объектов связности, введенных при определении удлиненной производной в общем случае. Для каждого индекса 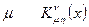представляет собой квадратную матрицу размером по числу компонент векторного поля 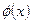и преобразующейся при преобразованиях:

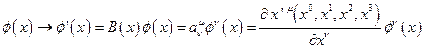, (4.26)

по закону, следующему из (3.8): .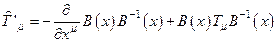

Приведенный закон преобразования объектов связности был получен как следствие требования: если 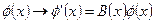, то:

.

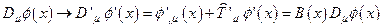Однако для случая преобразования компонент векторного поля с помощью матрицы А, это требование должно быть заменено иным. Дело в том, что для векторного поля 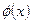его удлиненная производная 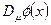является двухиндексным объектом и при координатных преобразованиях преобразовываться должна именно как двухиндексный объект. Потребуем, чтобы этот объект образовывал тензор: ковариантный по индексу дифференцирования 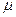и контравариантный по индексу, нумерующему компоненту поля, если поле – контравариантный вектор. Если же поле – ковариантный вектор, то 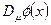представляет собой дважды ковариантный тензор.Тогда, закон для преобразования объектов связности получается из следующего правила: преобразованная удлиненная производная от преобразованного поля должна быть равна преобразованной по тензорному закону исходной удлиненной производной от исходной функции. Или:

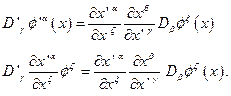
Последнее равенство можно переписать:

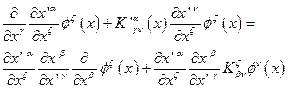(4.27)

Принимая во внимание, что:

,

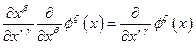получим:

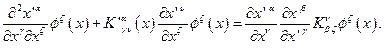
В последнем соотношении удобно штрихованные переменные и не штрихованные поменять местами. Тогда, учитывая, что:

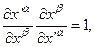
Можно получить закон преобразования афинных объектов связностипри координатных преобразованиях 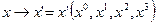. Для того чтобы уравнение (27) было выполнено, необходимо и достаточно, чтобы исходный и преобразованный объекты связности были связаны между собой соотношением:

(4.28)

Уравнение (28) представляет собой полный аналог калибровочных преобразований (17) для объектов связности общего вида учитывающий специфику координатных преобразований и следующих из них правил преобразований для векторов и тензоров. Преобразования (28) называются калибровочными преобразованиями афинных объектов связности. Также как и (17), они описывают законы преобразования но уже для частного случая - афинных объектов связности, характеризующих неоднородности среды. Два объекта связности калибровочно эквивалентны, если он связаны преобразованием (28) . Калибровочно-эквивалентным нулю называется объект связности, который может быть представлен в виде:

.

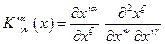Если афинный объект связности калибровочно-эквивалентный нулю, то существует координатное преобразование, переводящее его в тождественный ноль.

Наряду с ковариантной производной 4 контравариантного векторного поля:

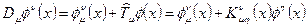(4.29)

Может быть определена ковариантная производная ковариантного векторного поля, т.е. поля с нижними индексами, преобразующегося при координатных преобразованиях по правилу (22):

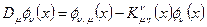. (4.30)

Это правило обеспечивает трансформационные свойства ковариантной производной ковариантного векторного поля, как дважды ковариантного тензора второго ранга при преобразовании афинных объектов связности по использованному уже правилу (28). Правила (30) «выводятся» из правила (29) и, наоборот, если предположить, что ковариантные вектора и контравариантные могут образовывать скалярные произведения по правилу 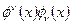. Скалярное произведение векторного поля самого с собой образует скаляр, ковариантная производная, от которого совпадает с обычной производной, и, кроме того, для скалярного произведения справедливо правило цепного дифференцирования так же, как и для обычной производной:

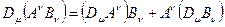. (4.31)

Нетрудно видеть, что сам афинный объект связности тензором не является, поскольку в закон его преобразования (28) входит «лишний» член:

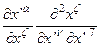
Отсюда, в частности, следует, что разность двух объектов афинной связности является тензором, но не является объектом афинной связности, а их сумма не является ни объектом связности, ни тензором 5. Однако выпуклая комбинация двух объектов связности является объектом связности.

Вид преобразования (28) наталкивает на рассмотрение только симметричной по нижним индексам афинной связности. Любая другая может быть представлена в виде симметричной и антисимметричной по нижним индексам компонент тензора третьего ранга:

.

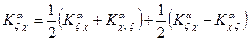В связи с тем, что свойство антисимметрии при преобразованиях (28) не сохраняется, рассмотрение таких связностей не дает новых результатов. Антисимметричная часть связности называется кручением. Оно переносится согласованно со связностью вектора. Далее будем предполагать, что все рассматриваемыми афинные связности симметричны по нижним индексам. В итоге кручение равно нулю.

Ковариантное дифференцированиепо переменной с индексом 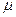будем обозначать добавлением к дифференцируемой величине соответствующего ковариантного индекса (в данном случае 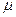) через точку с запятой (в отличие от обычного дифференцирования, обозначаемого через запятую): .

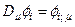Теперь можно определить удлиненную производную для тензора произвольного ранга какое-то количество раз ковариантному и какое-то количество раз контравариантного. Для каждого ковариантного индекса надо добавить «удлиняющий член производной» ковариантного типа, а для каждого контравариантного индекса –удлиняющий член контравариантного типа. Следующий пример пояснит сказанное:

,

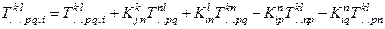Афинная связность порождает геометрические характеристики пространства, в частности, его кривизну. Повторяя рассуждения, приведшие к оператору кривизны в пространствах с локально нарушенной симметрией, в частности, к выражению (18), для оператора кривизны, получим:

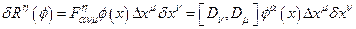(4.32)

Правая часть последнего выражения есть вектор, компоненты которого пронумерованы индексом 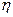. Этот индекс явно выписан лишь в правой части. Величина 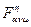, называется тензором кривизны или тензором Римана-Кристофеля. Если расписать это выражение, то получим:

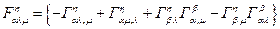(4.33)

Понятно, что если афинная связность калибровочно-эквивалентная нулю, то тензор кривизны тождественно равен нулю, что следует из тензорного закона преобразования кривизны. Если тензор кривизны равен нулю, то это означает, что согласованный со связностью и называемый потому параллельным, перенос вектора из точки в точку не зависит от пути переноса, а лишь от координат начальной и конечной точек. Это, в свою очередь, означает, что, исходя из заданного в одной точке вектора 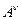, может быть построено векторное поле 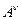(x) как результат параллельного переноса исходного вектора во все точки. Это векторное поле удовлетворяет уравнению 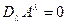или, что, то же самое:

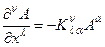. (4.34)

Если афинная связность задана и уравнение (34) разрешимо, то это означает равенство нулю кривизны и, как следствие, калибровочную эквивалентность нулю заданной афинной связности. В римановой геометрии такую связность называют интегрируемой.

В силу определения (32-33) кривизны – тензора Римана – Кристоффеля, имеют место следующие соотношения:

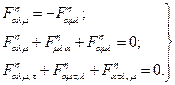(4.35)

Сворачивая тензор кривизны, получим тензор Ричи :

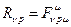
Кроме того:

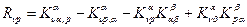. (4.36)

Его в свою очередь также можно свернуть по паре оставшихся индексов, получив тем самым хорошо известный в римановой геометрии объект – скалярную кривизну.

Введение афинных объектов связности порождает искривленное многообразие, которое можно представить как некоторую кривую поверхность, вложенную в некоторое пространство большего числа измерений. Геометрия этого пространства определяется линиями, перенесение вдоль которых касательных к этой линии векторов, согласованным со связностью образом, оставляет их касательными к той же линии. Такие линии называются геодезическими.

Пусть уравнение геодезической задано параметрическими уравнениями 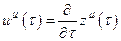. Приращение, которое получает контравариантный вектор 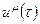при смещении на величину 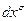равно:

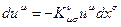. Откуда:

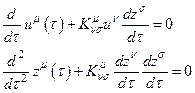(4.37)

Уравнение (37) представляет собой уравнение для геодезических.

Объекты афинной связности введены нами как частный случай калибровочных полей и объектов связности в пространствах с локально нарушенной симметрией. Однако аналогичная теория может быть построена на основе введения метрики в афинном пространстве, которая порождает объекты афинной связности. Рассмотрим элементы этой теории и продемонстрируем ее связь с вышеизложенным.

Пусть в афинном пространстве задан метрический тензор 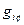второго ранга ковариантный и симметричный по своим индексам. Это означает, что для любых двух векторов А и В их скалярное произведение 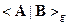определено соотношением 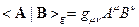. Соответствующим образом определена и длина вектора А: 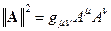. Афинное пространство, наделенное метрическим тензором, называется римановым пространством. Риманово пространство одновременно является и пространством с афинной связностью. При этом связность и метрика должны не противоречить друг другу. Соответствующая полю метрического тензора афинная связность, должна быть такой, чтобы согласованный со связностью перенос метрического тензора в другую точку дал результат, равный значению метрического тензора в этой другой точке, т.е. перенес его в себя. Это означает: 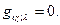Эквивалентным требованием служит то, что для любого контравариантного вектора 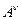величина 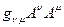должна оставаться инвариантом при всех одновременных переносах, как вектора 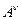, так и тензора 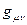. Если определить контравариантный метрический тензор 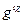условием 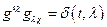6, то единственная афинная связность, удовлетворяющая таким условиям согласованности с метрикой, есть:

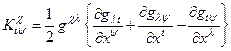. (4.38)

Однако найти обратное выражение далеко не всегда удается. Не всякое пространство с афинной связностью может быть римановым. Т.е. не для всякого афинного пространства может быть найден метрический тензор, соответствующая которому по (38) связность совпадает с исходной. Однако при этом римановы пространства, т.е. афинные пространства, снабженные метрическим тензором, представляют достаточно широкие возможности для описания неоднородностей среды через кривизну пространства. Использование с этой целью римановых пространств весьма просто. Достаточно в исходных уравнениях для однородной среды обыкновенные производные заменить ковариантным аналогом. Поскольку объекты связности по заданному метрическому тензору легко определяются, то проблем с расчетом первых производных, от скалярных и тензорных полей, не возникает. Сложности возникают при расчете вторых производных и, в частности, вычислении аналогов операторов Лапласа и Даламбера, имеющих в декартовых координатах вид:

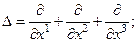
И соответственно

 .

Оба этих оператора можно записать в единой форме:

.

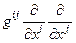В первом случае 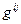диагональная 3х3 матрица с единичными элементами. Во втором это – диагональная 4х4 матрица, элементы 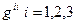которой равны единице, а элемент 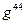равен минус единице. Для произвольного метрического тензора и скалярного поля F обобщением операторов Лапласа и Даламбера будет:

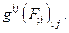
Непосредственной проверкой легко убедиться в том, что:

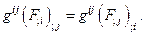
Несколько сложнее дело обстоит со вторыми производными для векторного поля. Можно показать, что:

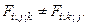
Обобщением этих операторов на случай векторного поля F служит [1]:

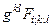, (4.39)

где:

.

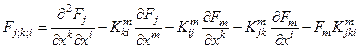Здесь: .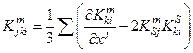

В том случае, если речь идет об операторе Даламбера, индексы меняются в пределах от нуля до трех. Для случая оператора Лапласа диапазон их изменения от единицы до трех.

Таким образом, неоднородная среда может характеризоваться искривлением пространственно-временной сцены, на которой происходит рассматриваемый физический процесс. Это задается с помощью задания зависящего от координат симметричного метрического тензора, через который с помощью соотношения (38) рассчитываются объекты афинной связности. Далее в уравнении, описывающем распространение поля в однородной и «плоской» среде, все производные заменяются их ковариантными аналогами. Наиболее часто встречающиеся операторы второго порядка, операторы Лапласа и Даламбера, заменяются выражениями (39). Восстановление компонент метрического тензора по наблюдаемым физическим полям составляет предмет задачи построения изображения среды.

4.3 Конструирование уравнений поля в пространствах с нарушенной симметрией.

Применим теперь технику, развитую в разделе 2 настоящего приложения для построений уравнений поля в пространствах с нарушенной симметрией. С этой целью рассмотрим, как распространяется уравнение для продольных волн в однородной среде на случай сред неоднородных. Волновое уравнение для потенциала 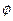продольных волн в однородной среде имеет вид:

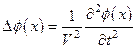. (4.40)

Требование однородности среды весьма существенно в процессе получения этого уравнения. В гл. 2 формулы (2.14-2.16) это продемонстрировано. Предположение о том, что среда неоднородна, влечет за собой появление производных по координатам от параметров упругости, разрастание и усложнение самого уравнения движения, и невозможность введения такого понятия, как переменная скорость. В то же время, экспериментально мы знаем, что такое переменная скорость и, хотелось бы знать, каким образом она может возникнуть из теоретических рассмотрений. Ответ на этот вопрос дает развитая выше техника характеристики параметров неоднородности как локального нарушения симметрии.

Волновому уравнению в однородной среде, которое мы намерены распространить, на неоднородные с локально нарушенной симметрией, соответствует лагранжева плотность:

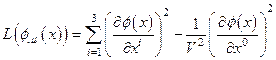(4.41)

В качестве группы Ли симметрий, локальное нарушение которой принимается за описываемую неоднородность, примем группу пространственно-временных трансляций. Генераторами этой группы, как было показано в приложении 3, в представлении на пространстве дифференцируемых функций служат операторы дифференцирования по соответствующей пространственной или временной координате - 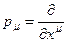. Заменяя в лагранжевой плоскости (41) обычные производные их удлиненными аналогами с использованием калибровочных полей и указанных генераторов:

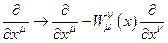, (4.42)

получим лагранжеву плотность для волнового уравнения в пространстве с нарушенной трансляционной симметрией:

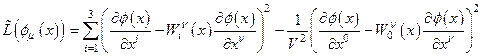. (4.43)

Уравнение Эйлера:

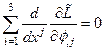
для лагранжевой плотности (42) запишется следующим образом:

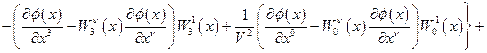
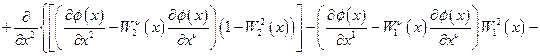
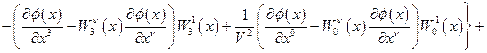
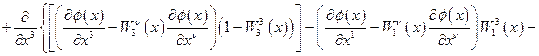
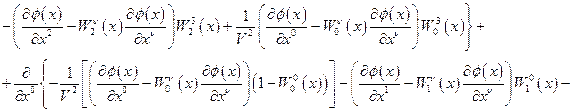
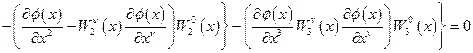. (4.44)

Уравнение (44) представляет собой весьма общее дифференциальное уравнение второго порядка с переменными коэффициентами, роль которых играют калибровочные поля 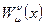. Таким образом, рассмотрение неоднородностей среды как искривления пространственно-временной сцены, на которой происходит распространение волн, приводит к общим дифференциальным уравнениям с переменными коэффициентами, связанными с калибровочными полями для соответствующих генераторов трансляций. Для произвольного дифференциального уравнения второго порядка может быть поставлена задача интерпретации коэффициентов этого уравнения как калибровочных полей, отвечающих за нарушение соответствующей симметрии.

Рассмотрим более частный случай уравнения (44), соответствующий предположению о локальном нарушении симметрии лишь относительно временных трансляций. Кроме того, будем считать неизменными во времени свойства симметрии рассматриваемого пространства. Это означает, что неоднородности среды не изменяются с течением времени на рассматриваемых временных масштабах. Тогда калибровочные полябудут не нулевыми лишь для 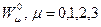и зависеть только от пространственных координат. Предположим, кроме того, 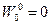. Последнее предположение связано с условием стационарности лишь в том случае, когда 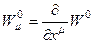, где 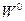некоторый потенциал объектов связности, зависящий от координат. Таким образом, используется лагранжева плотность:

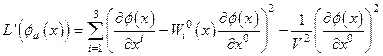(4.45)

уравнение Эйлера, для которой имеет вид:

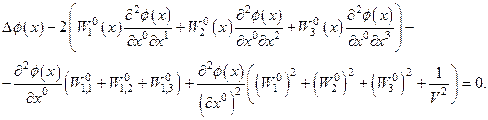(4.46)

Обозначим W векторнозначную функцию, компоненты которой, суть 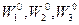. В частности, можно предположить, что 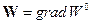. Тогда уравнение (46) можно переписать в форме:

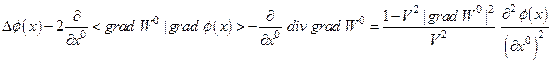. (4.47)

Или, что, то же самое:

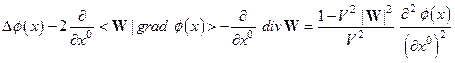(4.48)

Уравнения (47) и (48) представляют собой искомое обобщение уравнений распространения волн в однородной среде на случай среды, неоднородности которой состоят в локальном нарушении симметрии энергетических характеристик при временных трансляциях. Оператор кривизны, соответствующий указанному нарушению симметрии, имеет следующий вид:

. (4.49)

Здесь i,j =1,2,3. Очевидно, что 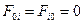и, следовательно, объекты связности калибровочно-эквивалентные нулю. Э
то означает существование потенциала для объектов связности, соответствующих нарушению симметрии относительно временных сдвигов, и нулевую кривизну для пространства, в котором происходит распространение волн.

Поскольку лагранжева плотность связана с энергетической характеристикой системы поле-неоднородность, то можно рассматривать коэффициенты 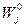как компоненты некоторого поля характеризующего состояние системы при заданном 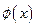. Тогда, считая лагранжеву плотность определенной, уравнением (4.43) варьируем (43) по 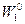в предположении экстремума. Получим в результате уравнения Эйлера:

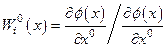, i=1,2,3. (4.50)

Пользуясь правилом дифференцирования неявно заданной функции, приходим к выводу, если существует функция 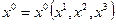, такая, ч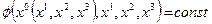то , то:

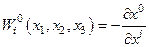. (4.51)

По смыслу функция 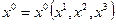для каждой точки пространства указывает время прихода возмущения в эту точку. Следовательно, коэффициенты 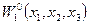, являясь компонентами градиента этой функции, характеризуют изменение «масштаба времени» в разных точках пространства при распространении волны.

Рассмотрим теперь случай, когда происходит нарушение симметрии по временным трансляциям, причем только 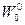отлично от нуля. Физически это означает искажение масштаба времени только во временной компоненте. Это соответствует введению лагранжевой плотности:

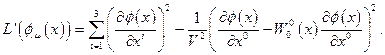(4.52)

Легко получить уравнение Эйлера для этого лагранжиана, которое имеет вид:

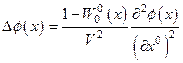. (4.53)

Волновое уравнение в среде с такого сорта неоднородностью имеет вид традиционно записываемого волнового уравнения с «переменой скоростью» 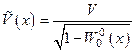. Отсюда, в частности, следует интерпретация переменной скоростив волновом уравнении как параметра нарушения симметрии по временным трансляциям – масштаба времени. Именно такой результат и требовалось получить. Волновое уравнение с переменной скоростью рассматривать можно, но переменная скорость возникает в результате модулирующего множителя 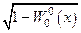при фоновой постоянной скорости, который имеет смысл искривления многообразия по временной компоненте параметра нарушения симметрии по временным трансляциям.

Рассмотрим далее уравнение Лапласав трехмерном пространстве:

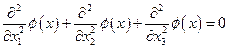. (4.54)

Лагранжева плотность, соответствующая этому уравнению имеет вид:

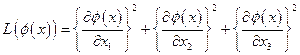. (4.55)

Введем в функцию 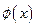дополнительный параметр x, в результате чего будем иметь 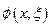. Лагранжева плотность симметрична относительно этого параметра просто потому, что она от него не зависит. Введем теперь нарушение симметрии относительно группы трансляций по этому параметру x. Это соответствует введению новой лагранжевой плотности L:

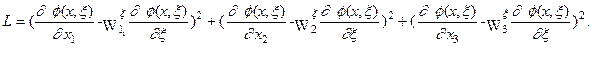
Записывая для этой лагранжевой плотности уравнение Эйлера, получим:

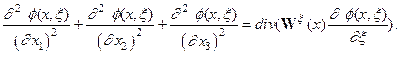
Здесь 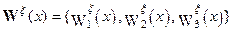- калибровочные поля, ответственные за характеристику локального нарушения симметрии относительно введенного параметра.

Рассмотрим частный случай, демонстрирующий возможные пути практического использования этого результата. Пусть среда характеризуется нарушением трансляционной симметрии только по вертикальной координате и в удлиненной производной калибровочное поле 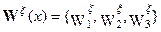имеет лишь отличную от нуля компоненту 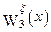. Это приводит к лагранжевой плотности

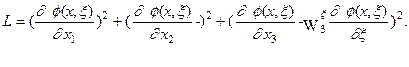
И уравнению Эйлера для нее:

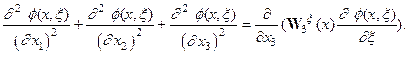(4.56)

В подобного рода задачах речь идет о реконструкциях параметров нарушения симметрии по результатам измерений поля, являющегося краевым значением гармонической функции. Отсюда, в частности, для (56) следует:

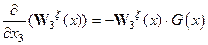, (4.57)

где: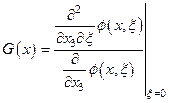

Поскольку измеряемая компонента поля должна соответствовать нулевому значению параметра 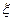, то можно считать заданной на уровне 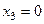функцию 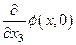, однако величина 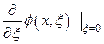и, следовательно, 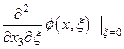остается неопределенной. Например, она может быть задана условием

.

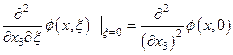Вычислив регуляризованное приближение к пространственному распределению функции 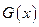, можно найти введенную характеристику нарушения симметрии пространства - 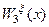, как решение задачи Коши (57) при дополнительном начальном условии 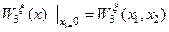. Это дает:

.

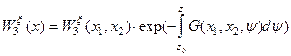Развитие подобного рода технологий открывает большое поле для деятельности. Приведенные соотношения и их обобщения могут быть использованы для интерпретации результатов эвристических трансформаций в терминах параметров нарушения свойств симметрии изучаемой среды. Действительно, выполнив процедуру построения пространственного распределения трансформанты поля, можно далее воспользоваться уравнениями поля с локально нарушенной симметрией и прямым вычислением, найти распределение калибровочного поля, обеспечивающего выполнимость уравнения для найденной трансформанты. Этот прием позволит перейти от пространственного распределения трансформанты поля к пространственному распределению параметра среды – нарушению симметрии, характеризующего меру неоднородности среды.

Литература.

1. Р.Рихтмаер Принципы современной математической физики, т.2.- М.:Мир, 1984.-С.246-249

Послесловие.

Геофизические методы весьма насыщены математикой. Это одна из наиболее математически емких областей практической инженерной и научной деятельности. Естественно в этой связи то, что в одном пособии охватить все аспекты этого вопроса в равной мере просто невозможно. Рассмотренные в учебном пособии математические основы теории интерпретации геофизических данных касаются, прежде всего, детерминированных и в меньшей мере эвристических моделей связей между «средой и полем». Это связано с тем, что методы построения содержательных моделей сред, а также построения их изображений за последние 10 – 15 лет получили существенное развитие. В то же время систематическое изложение математических основ этих методов не нашло должного отражения не только в учебной, но и научной монографической литературе. Редкое исключение – это монография Глазева В.Н [1]. Однако тираж этой и ей подобных книг таков, что рекомендовать его в учебном пособии – дело напрасное (в данном случае он равен 350 экз.) Кстати, точно также дело обстоит и с другими книгами. Так, упоминавшаяся в гл 2. великолепная книг Терещенко С.А. [2.1] имеет тираж 300 экз.

Что касается эвристических связей, лежащих в основе методов обработки данных и теории фильтрации геофизических полей, то меньшее внимание к ним продиктовано тем, что имеются прекрасные учебные пособия, и относительно доступная научная литература касающиеся этого вопроса [2-4]. Весьма полезна в этом отношении документация к распространенной в геофизической практике и доступной для получения системе «КОСКАД 3Dt» «КОМПЛЕКС СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННОГО АНАЛИЗА ДАННЫХ «КОСКАД 3Dt» Часть II. Авторы А.А. Никитин и А.В. Петров. Московский геологоразведочный университет. Последнее особо важно в связи с тем, что эта информация доступна в Internet.