Способы задания функции. Методические указания к типовому расчету

ГРАФИКИ ФУНКЦИЙ

Методические указания к типовому расчету

Омск-2002

Составители:

Бесценная Елена Владимировна, старший преподаватель

Воронцова Нина Александровна, старший преподаватель

Долганов Рудольф Леонидович, доцент

ВВЕДЕНИЕ

При исследовании различных явлений и процессов природы, решении технических задач, изучении математики, физики очень часто встречаются примеры изменения одной величины в зависимости от изменения другой – так называемой функциональной зависимости. Существуют различные способы задания функций: аналитический, словесный, табличный, но самым наглядным и наиболее распространенным является графический способ задания функции.

В средней школе изучаются в основном так называемые элементарные функции, построение графиков которых не составляет труда. При изучении высшей математики часто требуется знание большого числа самых разнообразных кривых и, что значительно важнее, умение строить их графики, исходя из их уравнений. Для построения кривых необходимо знать общие принципы и правила, пользуясь которыми можно нарисовать график данной линии. Ниже мы рассмотрим эти вопросы.

ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ

Понятие функции

Как известно, величины бывают переменные и постоянные. Например, при равномерном движении время и расстояние изменяются, а скорость остается постоянной; при нагревании газа в герметически закрытом сосуде давление и температура газа изменяются, а масса и объем не меняются.

При изучении разнообразных явлений природы, решении различных задач приходится рассматривать не столько переменные величины, взятые отдельно, сколько связь между ними, зависимость одной величины от другой.

В природе не существует переменных величин, которые изменялись бы изолированно, без связи с другими физическими величинами. Например, пройденный путь можно рассматривать с зависимости от изменения времени, т.е. путь является функцией от времени. Абстрагируясь от конкретных примеров зависимостей между конкретными величинами, в математике ввели понятие функциональной зависимости или функции.

Пусть даны два множества: Х и Y, элементами которых могут быть любые объекты, и допустим, что каждому элементу х множества Х по некоторому закону поставлен в соответствие один элемент множества Y, который обозначим у=f(x). Тогда f называется функцией из Х в Y (или отображением множества Х в Y). Таким образом, если задано отображение f множества Х в множество Y, то говорят, что на множестве Х определена функция f , которая принимает значения у=f(x) из множества Y. Множество Х называют областью определения функции f, а множество f(x) – множеством значений функции f. Очевидно, что f(x) Y. Переменную величину х называют независимой переменной или аргументом.

Y

d

y=f(x)

c

0 a x b X

Рис. 1.1

Равенство y = f (x) означает, что применив к значению аргумента х закон f, найдем соответствующее этому значению х, значение функции y = f(x).

На рис. 1.1 область определения функции у = f (x) – отрезок [а,b] и область значений функции – отрезок [с,d].

Способы задания функции

Задать функцию означает установить правило (закон) с помощью которого по данным значениям независимой переменной находим соответствующие им значения функции. Рассмотрим различные способы задания функции.

1. Табличный способ. При этом способе в определенном порядке выписываются ряд значений независимой переменной 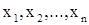и соответствующие им значения функции 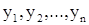. Таковы, например, таблицы логарифмов, таблицы значений тригонометрических функций и т.д. Табличный способ очень распространен в технике, естествознании и т.п. Численные результаты последовательных наблюдений какого-либо процесса или явления выписываются в виде таблицы. Например, результаты измерений температуры воздуха на метеорологической станции за один день оформляются так:

t, ч
Т, °С	-1	-2	-2,5	-2	-0,5				3,5

Эта запись определяет температуру Т как функцию от времени t: T = f (t). Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения функции сразу, без дополнительных изменений или вычислений. Недостатки: определяет функцию не полностью, а лишь для некоторых значений аргумента; не дает наглядного изображения характера изменения функции с изменением аргумента.

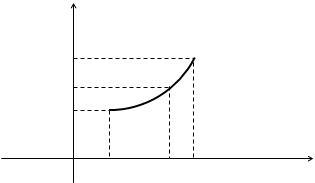
2. Графический способ. Графиком функции y = f (x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Это может быть некоторая кривая, в частности прямая, множество точек на плоскости.

Преимущество – наглядность, недостаток – нет возможности точно определить значения аргумента. В технике и физике часто он является единственно доступным способом задания функции, например, при пользовании самопишущими приборами, которые автоматически записывают изменение одной величины относительно другой (барограф, термограф и др.).

3. Аналитический способ. По этому способу функция задается аналитически, с помощью формулы. Такой способ дает возможность по каждому численному значению аргумента х найти соответствующее ему численное значение функции у точно или с некоторой точностью.

При аналитическом способе функция может быть задана и несколькими разными формулами. Например, функция

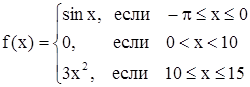
задана в области определения [- 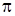, 15] с помощью трех формул.

Если зависимость между х и у задана формулой, разрешенной относительно у, т.е. имеет вид у = f (x) , то говорят, что функция от х задана в явном виде, например, 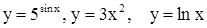. Если же значения х и у связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно у, то говорят, что функция задана неявно. Например, . Заметим, что не всякую неявную функцию можно представить в виде у = f(x), наоборот, любую явную функцию всегда можно представить в виде неявной: . Еще одна разновидность аналитического задания функции – параметрическое, когда аргумент х и функция у являются функциями третьей величины – параметра t: 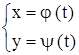, где , Т – некоторый промежуток. Такой способ широко применяется в механике, в геометрии.

Аналитический способ является самым распространенным способом задания функции. Компактность, возможность применения к данной функции аппарата математического анализа, возможность вычисления значений функции при любых значениях аргумента – его основные преимущества.

4. Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. Например, функция Е(х) – целая часть числа х, функция Дирихле, функция Римана, n!, r(n) – число делителей натурального числа n.

5. Полуграфический способ. Здесь значения функции представляются в виде отрезков, а значения аргумента – в виде чисел, проставленных на концах отрезков, указывающих значения функции. Так, например, в термометре есть шкала с равными делениями, у которых проставлены числа. Эти числа являются значениями аргумента (температуры). Они стоят на том месте, которое определяет графическое удлинение столбца ртути (значения функции) в связи с ее объемным расширением в результате температурных изменений.

Сложные функции

Пусть даны две функции: у = f(z), определенная на множестве z, и z =g(x), определенная на множестве х. Если 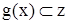; то на множестве Х можно определить функцию, которая каждому 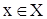поставит в соответствие 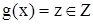. Тогда на множестве Х определена функция 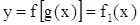. Эта функция называется сложнойфункцией х или суперпозицией (наложением) функций f и g.

Областью определения сложной функции является либо вся область определения функции z = g (x), либо та ее часть, в которой определены значения z, не выходящие из области определения f(z). Например, пусть 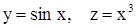. Функция 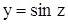определена на всей числовой оси, функция 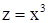также определена на всей числовой оси. Суперпозиция этих функций является сложной функцией х , определенной на всей числовой оси.

При рассмотрении сложных функций следует иметь в виду области определения составляющих функций. Например, из функци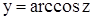й и 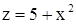нельзя образовывать сложную функцию, так как функция y = arcсos z определена для , а функция , т.е. не принадлежит этому отрезку.

Можно рассматривать суперпозиции не только двух, но и трех, четырех, т.е. любого конечного числа функций.

Обратные функции

Функция y = f(x) называется обратимой, если она принимает каждое свое значение один раз. Пусть f – отображение множества Х на множество Y. Если для любого элемента у из Y существует единственный элемент х=g(y), для которого f(x)=y, то отображение f называется обратимым. Отображение, обратное к у, обозначается 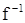и называется обратной функцией, а функция y = f(x) называется прямой функцией. Например, функция 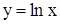имеет обратную функцию 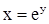, а для функции у = х³ обратной будет 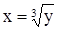. Не всякая функция имеет обратную. По графику прямой функции у=f(x) достаточно просто определить, имеет ли эта функция обратную. 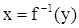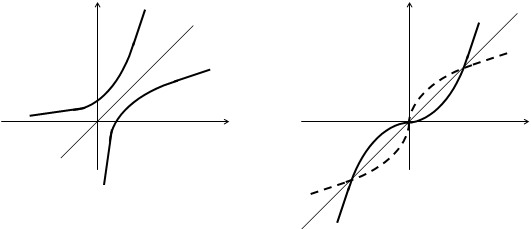Если какая-либо прямая, параллельная оси ОХ, пересекает график прямой функции не более чем в одной точке, то обратная функция существует. Если же хотя бы одна из таких прямых пересекает график функции в двух или более точках, то обратная функция не существует. Если построить прямую и обратную функции в одной системе координат, то их графики будут симметричны относительно прямой - биссектрисы I и III коор-динатных углов. На рис. 1.2 и 1.3 приведены примеры.

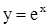Y Y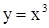

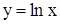
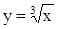
Рис. 1.2 Рис. 1.3