Тема 4. Повторение - решение задач графическим методом. Симплекс-метод решения ЗЛП

Задание. Решить графическим методом следующие задачи:

Задача 1.	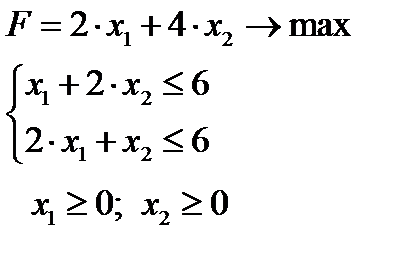Задача 2.	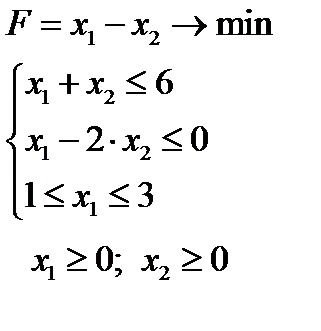Задача 3.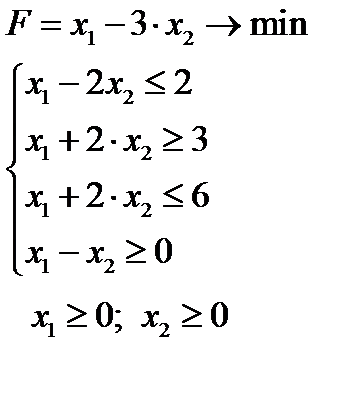
Задача 4.	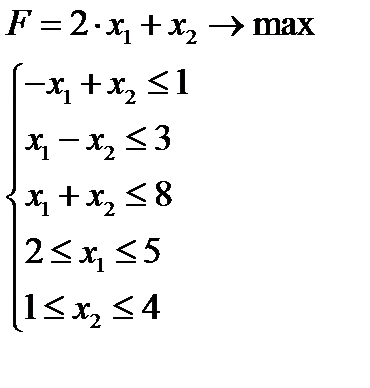Задача 5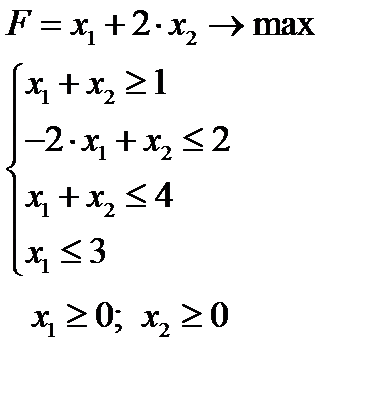
Симплекс-метод решения ЗЛП Цель занятия: овладение студентами симплекс-методом решения ЗЛП. Задачи занятия: - изучение правил построения симплекс-таблицы; - получение навыка решения ЗЛП с помощью симплекс-таблиц. Методические указания Симплекс метод – основной, универсальный метод, которым можно решить любую задачу ЛП. Симплекс метод представляет собой схему перехода от одного базисного решения к другому, третьему и так далее, пока не будет найдено

Симплекс метод – основной, универсальный метод, которым можно решить любую задачу ЛП.

Симплекс метод представляет собой схему перехода от одного базисного решения к другому, третьему и так далее, пока не будет найдено оптимальное решение либо не будет установлено, что система ограничений противоречива.

Применение симплексного метода разбивается на два этапа.

П е р в ы й э т а п. Получение допустимого базисного решения, если исходное базисное решение недопустимое, или установление несовместности системы ограничений (на этом этапе целевая функция не рассматривается).

Рассмотрим на примере определение базисного решения

Пример 1.

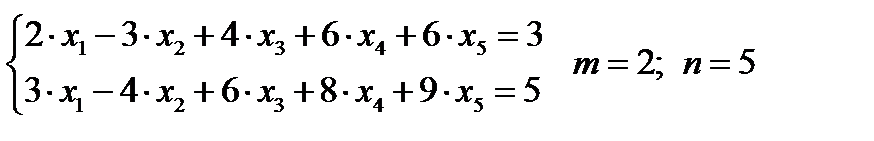
Любые “m” переменных из m уравнений с n переменными (m < n) называются основными, если определитель из коэффициентов при них отличен от нуля

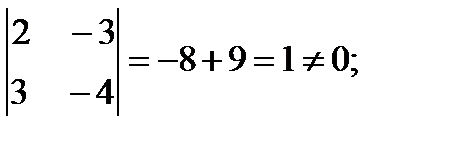Х₁,Х₂ – основные переменные, а Х₃, Х₄, Х₅ – неосновные. Базисными называются решения системы из m уравнений с n неизвестными (m < n), в которых неосновные переменные имеют нулевые значения. Выразим основные переменные через неосновные. Оставим слева только основные переменные, а все остальные перенесем вправо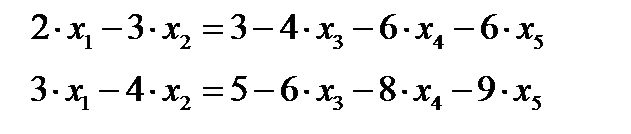

домножим первое и второе уравнения на дополнительные множители

и методом алгебраического сложения получим:

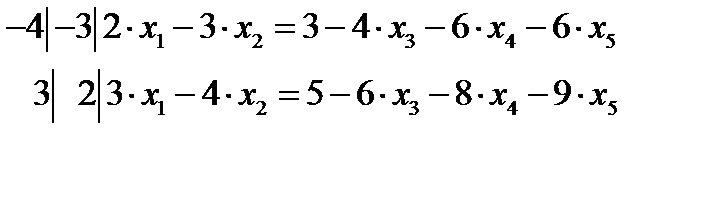
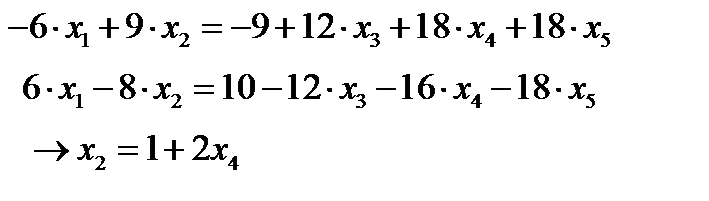
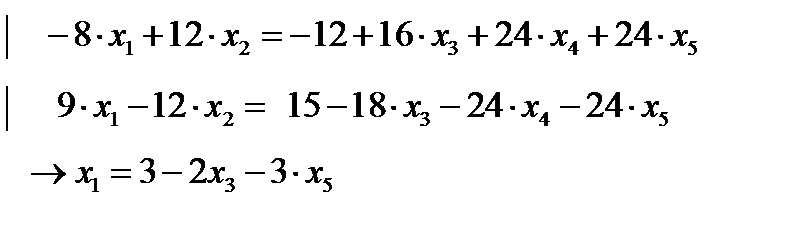
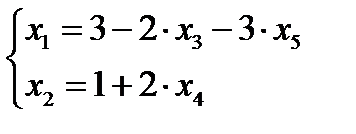Первое базисное решение (3;1;0;0;0)

Проверим Х₁ и Х₃ в качестве основных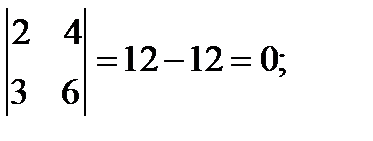

Проверим Х₁ и Х₄ в качестве основных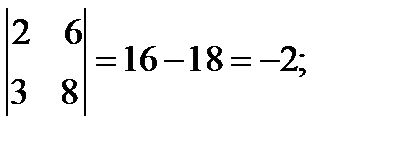

Х₁,Х₄ – основные переменные, а Х₂, Х₃, Х₅ – неосновные.

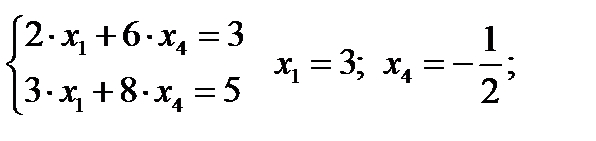Второе базисное решение (3;0;0; 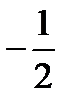;0)

Аналогично найдем еще четыре базисных решения:

(0;1; 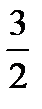0;0;0); (0;1;0;0;1); (0;0; 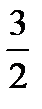; ;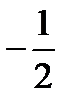0); (0;0;0; 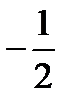;1)

Выделим среди базисных решений те, где компоненты неотрицательны – оно называется допустимым (опорным). Если хотя бы одна компонента отрицательна, то решение называется недопустимым.

Найти самостоятельно базисные решения системы и указать допустимые или доделать дома.

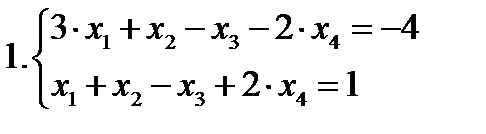
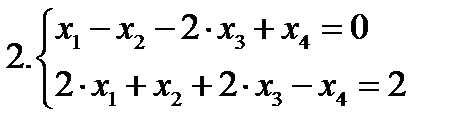
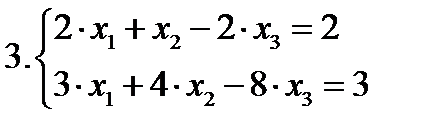
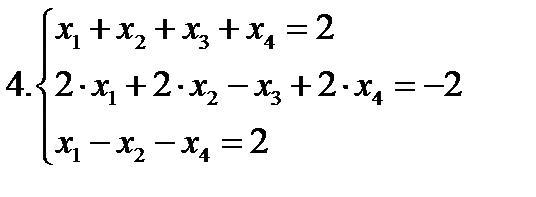
Пример 2. Даны системы ограничений трех задач ЛП:

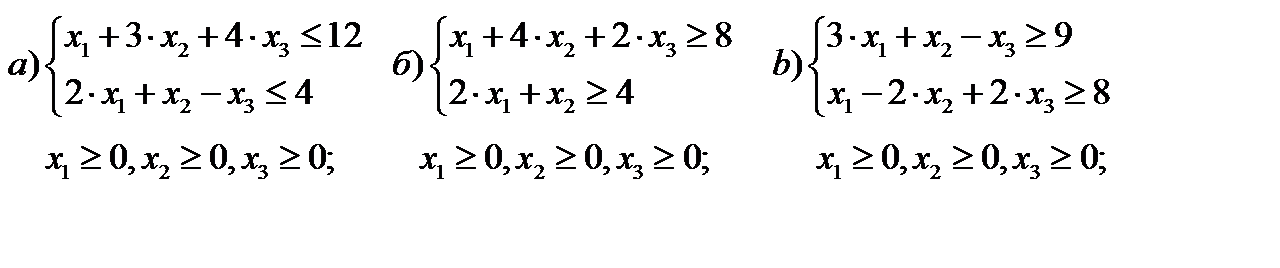
Найти допустимое базисное решение.

Решение. (а) Введем дополнительные переменные Х₄ и Х₅ (со знаком плюс, так как все неравенства вида ( 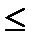) и представим данную систему неравенств в виде эквивалентной системы уравнений

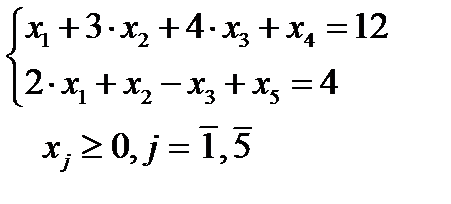
В качестве основных берем переменные, каждая из которых входит только в одно уравнение системы, т.е. дополнительные переменные -

Х₄ и Х_5.

1 шаг.Основные переменные - Х_{4 ,}Х₅ ; неосновные переменные Х₁ ;Х₂ и Х_{3 .} Выражая основные переменные через неосновные, получим

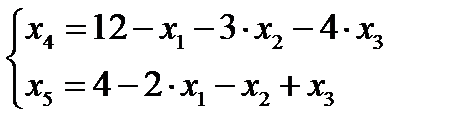
Приравнивая к нулю неосновные переменные Х₁;Х₂ и Х₃ найдем базисное решение (0;0;0;12;4), которое является допустимым.

(б) Введем дополнительные переменные Х₄ и Х₅ ( со знаком минус, т.к. все неравенства вида ( 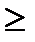) . Получим

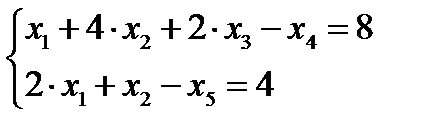
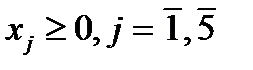
Здесь в качестве основных переменных брать дополнительные переменные Х₄ и Х₅ невыгодно: они входят в левые части уравнений с отрицательными компонентами.

Целесообразно в качестве основных взять переменную Х₃ и дополнительную переменную Х₅. Переменная Х₃ также входит только в одно уравнение системы, но, в отличие от Х₄ с положительным коэффициентом. Это приведет также к недопустимому базисному решению, но лишь с одной отрицательной компонентой.

1 шаг.Основные переменные – Х_{3 ,}Х₅ ; неосновные переменные Х₁ ;Х₂ и Х_{4 .} Выражая основные переменные через неосновные, получим

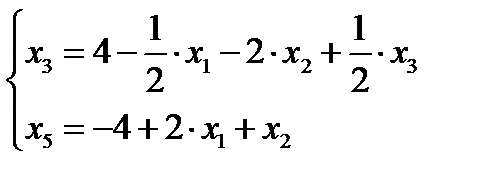базисное решение (0;0;4;0;-4) – недопустимое.

Для получения допустимого базисного решения нужно перевести в основные переменную, которая в уравнении с отрицательным свободным членом (во втором уравнении) имеет положительный коэффициент, т.е. Х₁или Х₂.

Если переводить в основные переменную Х₁ , то ее максимальное значение определяется из условия

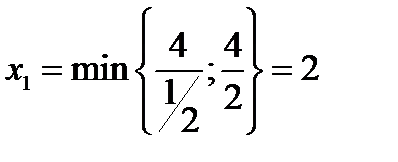
В этом случае выделяется второе уравнение и в неосновные переводится переменная Х₅.

Если переводить в основные переменную Х₂, то ее максимальное значение определяется из условия

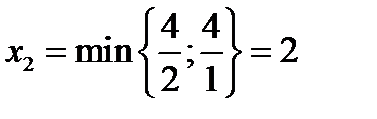
Т.е. выделяется первое уравнение и в неосновные переводится переменная Х_3.

Какую же переменную выгоднее перевести в число основных? При возможности выбора переводим в основную ту переменную, для которой выделенное уравнение имеет отрицательный свободный член. Это гарантирует уменьшение (по крайней мере на единицу) числа отрицательных компонент в новом базисном решении, в противном случае их число сохранится прежним.

Итак, переводим в основные переменную Х₁. При Х₁=2, как видно из уравнения 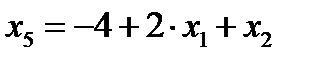, переменная Х₅ = 0 переходит в число неосновных.

2 шаг. Основные переменные – Х_{1 ,}Х₃ ; неосновные переменные Х₂ ;Х₄ и Х_{5 .}

Выражаем новые основные переменные через новые неосновные, начиная с последнего:

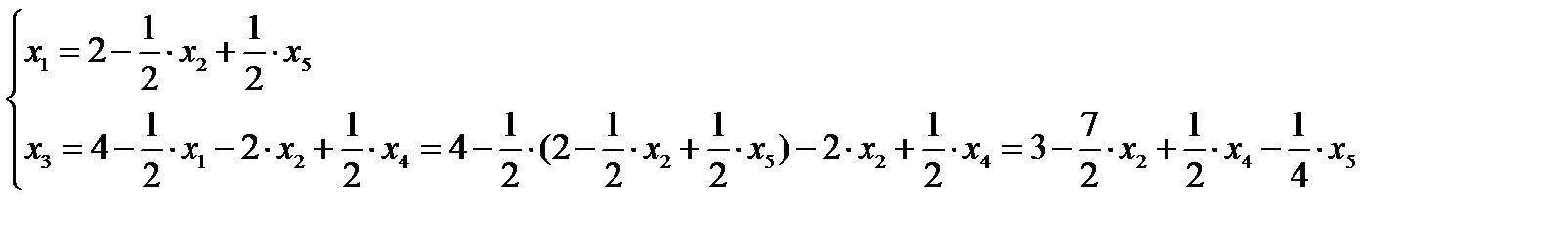
или

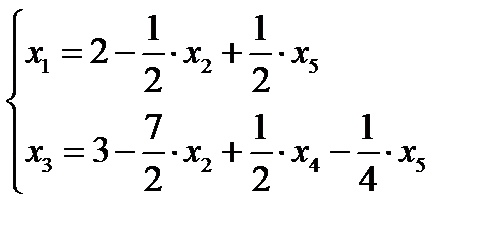
Второе базисное решение (2;0;3;0;0) – допустимое.

Замечание.Если бы мы перевели в основную переменную Х₂, то, как нетрудно убедиться, получили бы новое базисное решение (0;4;-4;0;0), являющееся по-прежнему недопустимым, и для нахождения допустимого базисного решения потребовался бы дополнительный шаг.

(в) Вводя дополнительные переменные, приведем систему ограничений к виду

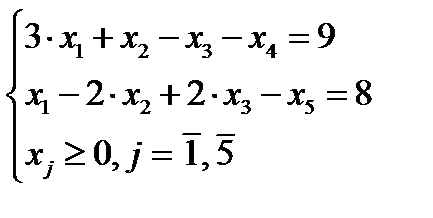
1 шаг.Основные переменные – Х_{4 ,}Х₅; неосновные переменные Х₁ ;Х₂ и Х_{3 .} Выражая основные переменные через неосновные, получим

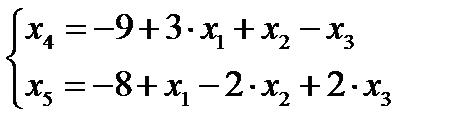
Первое базисное решение (0;0;0;-9;-8) – недопустимое.

Переводим в основные, например, переменную Х₁ (она входит с положительным коэффициентом в выражение для основных переменных Х_{4 ,}Х₅ содержащие отрицательные свободные члены). Найдем

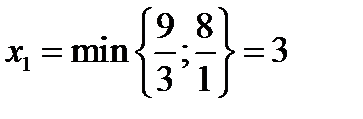т.е. выделяем первое уравнение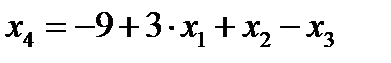

При Х₁ = 3 переменная Х₄ = 0 и переходит в число неосновных.

2 шаг. Основные переменные – Х_{1 ,}Х₅ ; неосновные переменные Х₂ ;Х₃ и Х_{4 .}После преобразования получим

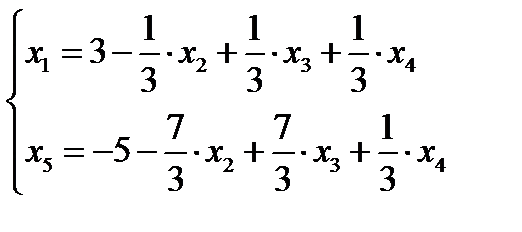
Второе базисное решение (3;0;0;0;-5) – недопустимое, но лучше первого, так как содержит на одну отрицательную компоненту меньше. По соображениям, приведенным в предыдущей задаче, в основные можно перевести либо переменную Х₃, либо Х₄. Переводим в основные переменные Х₄, поскольку это позволяет упростить преобразования:

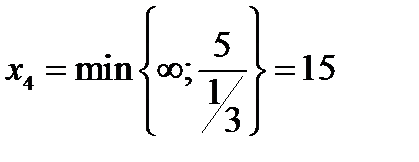( для первого уравнения отношение равным 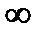, т.к.

переменная Х₄ входит в него с тем же (положительным) знаком, что и свободный член). Выделяем второе уравнение, из которого видно, что при

Х₄ = 15 переменная Х₅ = 0 переходит в число неосновных.

3 шаг. Основные переменные – Х_{3 ,}Х₄; неосновные переменные Х₁ ;Х₂ и Х_{5 .} Третье базисное решение (8;0;0;15;0) – допустимое.

Пример 3. Дана система ограничений одной из задач ЛП (в канонической форме):

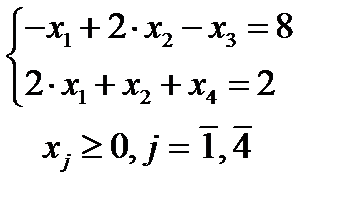Показать, что данная система несовместна.

Р е ш е н и е.1 шаг. Основные переменные – Х_{3 ,}Х₄; неосновные переменные Х₁ ;Х_2.

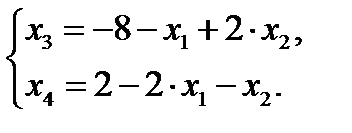Первое базисное решение (0;0;-8;2) –недопустимое.

Перевести в основные можно только переменную Х₂, которая входит с положительным коэффициентом в уравнение, имеющее отрицательный свободный член:

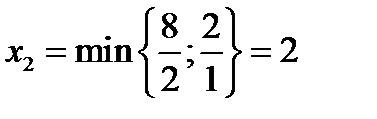Выделяем второе уравнение. При Х₂ = 2 переменная Х₄ = 0 и переходит в число неосновных.

2 шаг. Основные переменные – Х_{2 ,}Х₃; неосновные переменные Х₁ ;Х_{2 .}

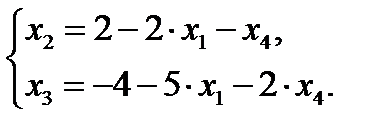
Второе базисное решение (0;2;-4;0) вновь недопустимое, так как выделенным на 1 шаге оказалось уравнение с отрицательным свободным членом. Однако получить лучшее решение уже нельзя, потому что во втором уравнении и свободный член, и коэффициенты при всех неосновных переменных отрицательны. Следовательно, задача не имеет ни одного допустимого базисного решения, т.е. система ее ограничений несовместна.

В т о р о й э т а п.Нахождение оптимального решения.

На этом этапе важно установить: является ли найденное оптимальное решение единственным, или произойдет нарушение его единственности; будет ли целевая функция иметь конечный оптимум, или она не ограничена.

Решим три задачи на нахождение минимума, в которых первый этап решения уже завершен:

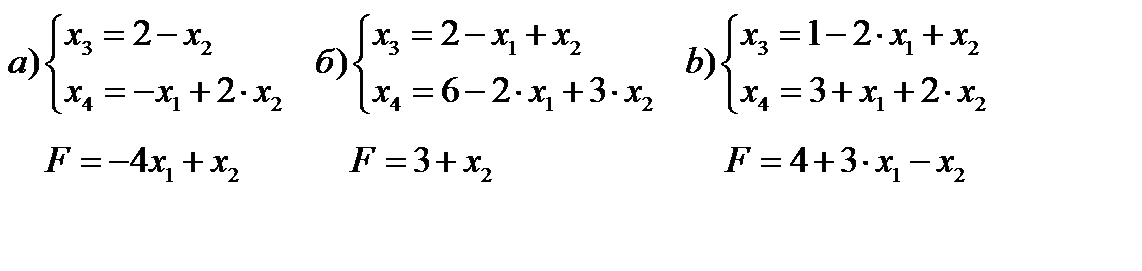
Закончить решение задачи.

Р е ш е н и е. (а) Базисное решение (0;0;2;0) – вырожденное (основная переменная Х₄ = 0) и не оптимальное, так как переменная Х₁ входит в выражение линейной функции с отрицательным коэффициентом. Чтобы минимизировать линейную функцию переведем переменную Х₁ в основные. Тогда

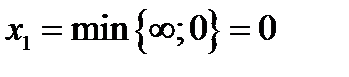
Первое отношение считаем условно равным 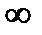, так как переменная Х₁

в первом уравнении отсутствует. Второе отношение равно нулю, ибо свободный член второго уравнения равен нулю, а переменная Х₁ входит в него с отрицательным коэффициентом.

Выделяем второе уравнение. При Х₁ = 0 переменная Х₄ = 0 и переходит в число неосновных. Делаем следующий шаг.

Основные переменные – Х_{1 ,}Х₃; неосновные переменные - Х₂ ;Х₄

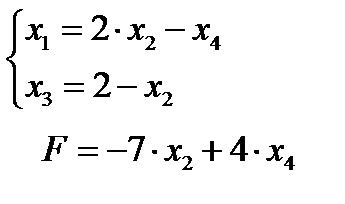
Получили новое базисное решение (0;0;2;0) – такое же, как и на предыдущем шаге (только теперь равна нулю основная переменная Х₁). Соответственно не изменилось и значение линейной функции. И это естественно, так как переменная Х₁ по-прежнему равна нулю, хотя теперь и является основной. Однако такой формальный шаг с переводом Х₁ в основные является вынужденным для дальнейшего решения задачи.

Для получения улучшенного решения переводим в основные переменную Х₂ , которая входит в выражение линейной функции с отрицательным коэффициентом:

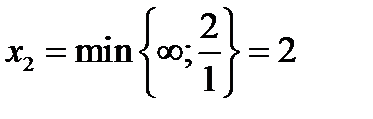
Обратите внимание на то, что и в данном случае первое отношение считается условно равным 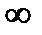: хотя свободный член в первом уравнении и равен нулю, но переменная Х₂ входит в это уравнение с положительным коэффициентом, т.е. первое уравнение не ограничивает рост переменной Х₂ . Выделяем второе уравнение. При Х₂ =2 переменная Х₃ =0; переведем ее в число неосновных, а затем переходим к следующему шагу.

Основные переменные – Х_{1 ,}Х₂; неосновные переменные - Х₃ ;Х₄ . После преобразований

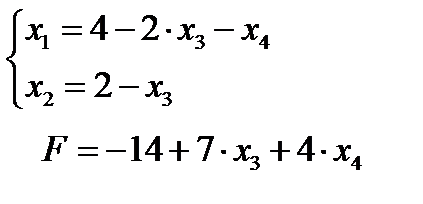
Новое базисное решение (4;2;0;0) является оптимальным, т.к. в выражении линейной функции нет основных переменных с отрицательными коэффициентами. Находим оптимум линейной функции: 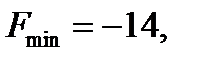при оптимальном базисном решении (4;2;0;0).

б) Базисное решение (0;0;2;6) – оптимальное, т.к. выполнен критерий оптимальности (для случая минимизации линейной функции). Оптимум линейной функции 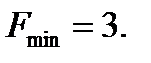В выражении для линейной функции отсутствует неосновная переменная Х₁, то оптимальное решение не единственное (т.е. существует бесконечное множество оптимальных решений, среди которых конечное число базисных оптимальных решений). Получим эти решения.

Какой бы ни была переменная Х₁ , удовлетворяющая данной системе ограничений, при Х₂=0 оптимальное значение линейной функции одно и тоже: 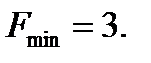Переменная Х₁ ,может принимать значения

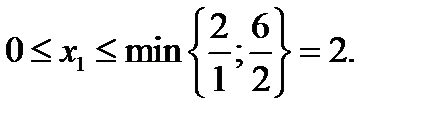
Для получения всех оптимальных решений выразим все переменные через Х₁ , считая, что Х₂=0, и полагая что Х₁ =С.

Ответ. 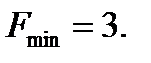при оптимальных решениях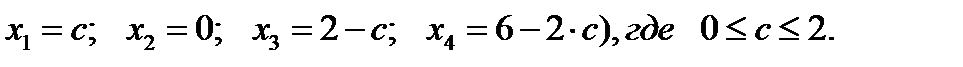

b) Базисное решение (0;0;4;3) - не оптимальное, т.к. не выполнен критерий оптимальности. Переведем в число основных переменную Х₂, которая входит в выражение для линейной функции с отрицательным коэффициентом. Найдем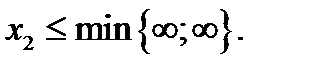

Полученные отношения означают, что оба уравнения не ограничивают рост переменной Х₂, т.е. линейная функция F, будучи отрицательной по знаку, неограниченно возрастает по абсолютной величине. Итак, задача не имеет конечного оптимума, т.е.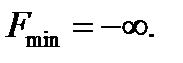

Рассмотрим алгоритм решения задач симплексным методом.

1. Математическая модель задачи должна бать канонической. Если она неканоническая, то ее надо привести к каноническому виду.

2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплекс-таблицу. Все строки таблицы 1-го шага, за исключением строки D_j (индексная строка), заполняем по данным системы ограничений и целевой функции. Симплексная таблица будет иметь следующий вид:

сi	Сj	С1	с2	¼	сm	сm+1	¼	сn	f(`X)
Базисная переменная (БП)	x1	x2	¼	xm	xm+1	¼	xn	b1
c1	x1			¼		h1, m+1	¼	h1n	l1
c2	x2			¼		h2, m+1	¼	h2n	l2
¼	¼	¼	¼	¼	¼	¼	¼	¼	¼
cm	xm			¼		hm, m+1	¼	hmn	lm
	Dj			¼		Dm+1	¼	Dn	f(`X1)

Индексная строка (D_j) для переменных находится по формуле

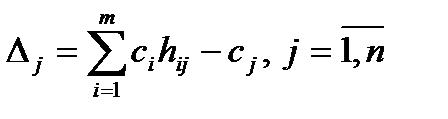
и для свободного члена по формуле

.

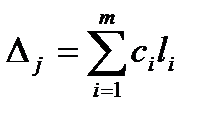При этом возможны следующие случаи решения задачи на максимум:

- если все оценки D_j ³ 0, то найденное решение оптимальное;

- если хотя бы одна оценка D_j £ 0, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращают, так как f(X) ® ¥, т.е. целевая функция не ограничена в области допустимых решений;

- если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;

- если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Пусть одна оценка D_k £ 0 или наибольшая по абсолютной величине D_k £ 0, тогда k-й столбец принимают за разрешающий. За разрешающую строку принимают ту, которой соответствует минимальное отношение свободных членов (b_i) к положительным коэффициентам k-го столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называют ключевым (разрешающим) элементом.

3. Заполнение симплексной таблицы 2-го шага:

- переписывается ключевая строка, разделив ее элементы на ключевой элемент;

- заполняют базисные столбцы;

- остальные коэффициенты таблицы находят по правилу «прямоугольника». Оценки можно считать по приведенным выше формулам или по правилу «прямоугольника». Получается новое опорное решение, которое проверяется на оптимальность и т.д.

Примечание. Если целевая функция f(X) требует нахождения минимального значения, то критерием оптимальности задачи является неположительность оценок D_j при всех .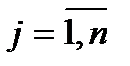

Правило «прямоугольника» состоит в следующем. Пусть ключевым элементом 1-го шага является элемент 1-й строки (m+1)-го столбца h_{1, m+1}. Тогда элемент i-й строки (m+2)-го столбца 2-го шага, который обозначим 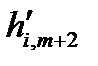, по правилу «прямоугольника» определяется по формуле

,

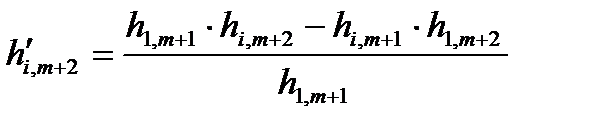где h_{1, m+1}, h_{i, m+1}, h_{i, m+2} – элементы 1-го шага.

Пример 4. Разберем решение примера 1 симплекс-методом

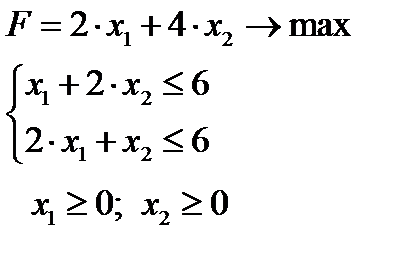
Запишем систему ограничений в канонической форме:

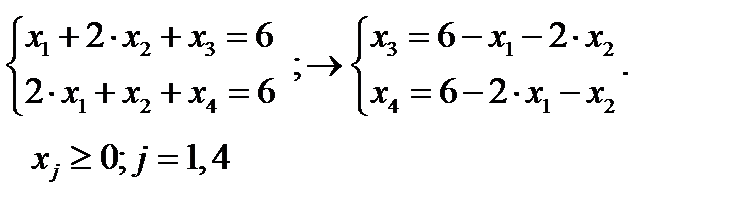Найдем первое решение 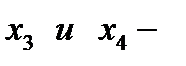основные переменные, а 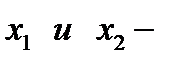неосновные. Пусть неосновные переменные равны нулю, тогда 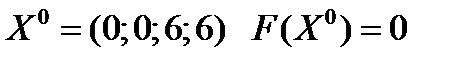решение допустимое, т.к. все координаты положительны. Можно переходить ко второму этапу – оптимизации. Построим такую таблицу:

сi	сj		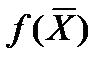				Примечания
Базисные переменные (БП)	х1	х2	х3	х4	bi
	х3
	х4
Dj	-2	-4

Т.к. в индексной строке две отрицательных переменных и задача на максимум, то необходимо в базис перевести ту их них, которая больше влияет на целевую функцию и это х₂. Определим, из какого уравнения это лучше сделать. Для этого найдем разделим свободный член b на коэффициент при х₂ во втором столбце и выберем минимум:

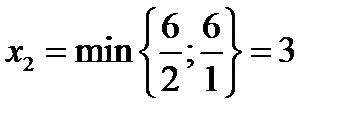
Получается, что из первого уравнения. Выберем х₂ = 2 за разрешающий элемент и выделим его. Вся строка, в которой содержится разрешающий элемент, будет называться разрешающей. Продолжаем заполнять таблицу.

Все элементы первой строки разделим на разрешающий, получим:

сi	сj		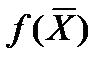				Примечания
Базисные переменные (БП)	х1	х2	х3	х4	bi
	х3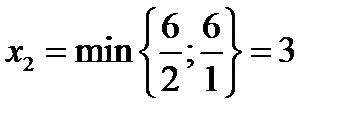
	х4
Dj	-2	-4
	х2	1/2		1/2
	х4
Dj

х₂ – переводим в базис, значит в других уравнениях х₂ = 0. Чтобы заполнить вторую строку до конца воспользуемся правилом прямоугольника.

сi	сj		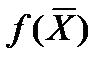				Примечания
Базисные переменные (БП)	х1	х2	х3	х4	bi
	х3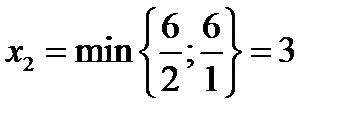
	х4
D1	-2	-4
	х2	1/2		1/2
	х4	3/2		-1/2
D2

Во второй индексной строке нет отрицательных значений, значит найденное значение 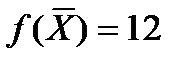оптимальное, а .

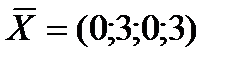Дома сделать следующие задания

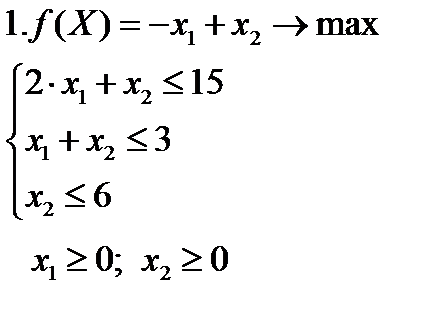
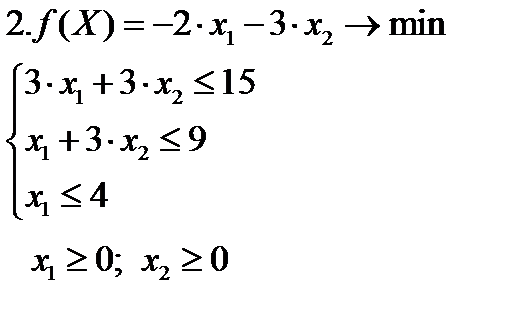
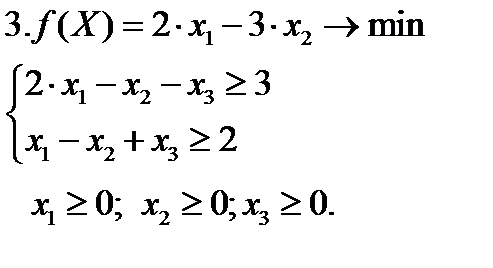
4. Для изготовления шкафов и буфетов деревообрабатывающий комбинат применяет древесину 4-х видов. Запасы древесины по каждому виду ограничены и составляют соответственно 120, 160, 120, 80 единиц. Количество единиц древесины каждого вида, необходимое для изготовления одного шкафа и одного буфета, а также прибыль от реализации даны в табл.

Таблица 1

Вид древесины	Запас древесины	Количество единиц древесины, необходимое для производства ед. продукции
	Шкафы	Буфеты
I II III IV
Прибыль

Составить математическую модель задачи и решить ее симплекс методом.