Раздел 3.4. Диффузионная модель

Поршневой режим движения жидкостей, рассмотренный нами при выводе уравнения модели идеального вытеснения, в реальных процессах реализуется не всегда. На самом деле в реальных процессах жидкость в различных направлениях перемещается за счет следующих явлений:

· Турбулентности потока

· Конвективного переноса.

· Поперечной неравномерности профиля скорости.

· Пристеночных эффектов, каналообразования.

· Переноса за счет молекулярной диффузии.

Будем считать, что все отклонения режима движения от поршневого могут быть сведены к переносу в обратном направлении за счет влияния конвективной диффузии, или осевой дисперсии.

Составим при этих допущениях уравнение материального баланса для элементарного объема проточного аппарата подобного аппарату идеального вытеснения, только с учетом диффузии в обратном направлении. На рис 3.10. приведена схема потоков в таком аппарате:

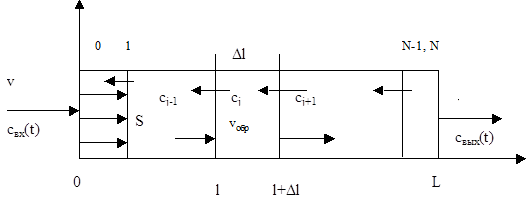
Рис.3.4.1. Схема потоков в аппарате, описываемом диффузионной моделью.

V=S×L – объем аппарата, S=p×d²/4 – площадь поперечного сечения, L – длина аппарата. Стрелками в обратном направлении обозначен перенос вещества в обратном направлении за счет конвективной диффузии или продольной дисперсии.

Поток вещества за счет турбулентной диффузии описывается уравнением, подобным уравнению диффузии Фика:

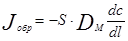(3.4.1)

Где J_обр- поток вещества в обратном направлении.

D_M – коэффициент обратного переноса массы за счет турбулентной диффузии.

Составим уравнение материального баланса для элементарного объема аппарата, ограниченного сечениями j-1 и j+1, расположенными на расстоянии Dl.

Приход вещества в рассматриваемый объем складывается из прихода за счет конвективного переноса, равного произведению v×c_j-1 и приходу за счет обратного потока из предшествующего объема аппарата:

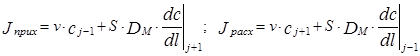(3.4.2)

Накопление массы в рассматриваемом элементарном объеме будет равно интегралу от разности входящего и выходящего потоков в объем:

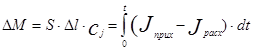(3.4.3)

Перейдем теперь от накопления массы в объеме к изменению концентрации. Для этого разделим обе части уравнения на величину элементарного объема

DV=S×Dl и продифференцируем обе части уравнения по времени. Уравнение принимает следующий вид, с учетом того, что производная от интеграла по аргументу равна подинтегральному выражению и с учетом выражений уравнения (3.4.2) для потоков прихода и расхода вещества:

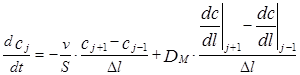(3.4.4)

Рассмотрим пределы слагаемых правой части уравнения (3.4.4) при Dl®0.

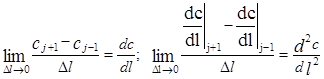(3.4.5)

Подставив выражения пределов из (3.4.5) в (3.4.4) получим окончательно уравнение диффузионной модели в следующем виде:

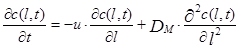(3.4.6)

Уравнение записано как дифференциальное уравнение в частных производных, так как концентрация является функцией двух независимых переменных с(l,t). В дальнейшем мы не будем это писать для сокращения записей но будем постоянно иметь в виду, что с=с(l,t).

Приведем уравнение к безразмерному виду с помощью следующих подстановок:

x=l/L, где l – текущая длина, а L – полная длина аппарата. Тогда Ldx=dl и dl²=L²dx². С использованием этих подстановок уравнение диффузионной модели может быть преобразовано к следующему виду:

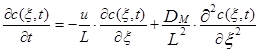(3.4.7)

Умножим обе части уравнения (3.4.7) на величину L/u= 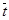- среднее время пребывания в аппарате. В итоге получим:

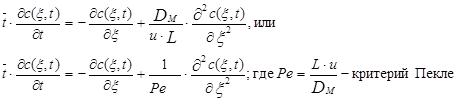(3.4.8)

Рассмотрим предельное выражение уравнения диффу4зионной модели при Ре® ¥. При Ре® ¥ 1/Ре®0. Таким образом уравнение диффузионной модели превращается в следующее уравнение:

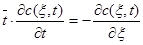, которое является уравнением модели идеального вытеснения.

Для решения уравнения диффузионной модели преобразуем его по Лапласу по переменной t. В итоге получим:

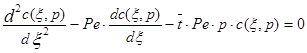(3.4.9)

Уравнение (3.4.9) представляет собой однородное обыкновенное дифференциальное уравнение с постоянными коэффициентами. Для его решения необходимо решить характеристическое уравнение, в котором К есть d/dx. Характеристическое уравнение для уравнения (3.4.9) будет иметь вид:

K²-Pe×K- 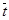×Pe×p=0 (3.4.10)

Найдем корни характеристического уравнения в следующем виде:

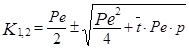(3.4.11)

Обозначим первое слагаемое в уравнении (3.4.1) через a, а второе через b.

Тогда корни характеристического уравнения можно записать в следующем виде: К₁ = a+b, К₂ = a - b . Тогда общее решение уравнения (3.4.9) для случая когда К₁ ¹ К₂ (корни различные и действительные) можно записать в виде:

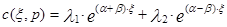(3.4.12)

где -l₁ и l₂ – постоянные интегрирования, определяемые из граничных условий.

Если К₁ = К₂ (корни равные и действительные)

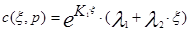(3.4.13)

Если корни комплексные К_1,2=a±i×b - a- действительная часть, i×b -мнимая часть, то решение имеет вид:

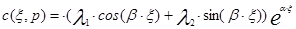(3.4.14)

Найдем граничные условия для аппарата конечных размеров. Для этого составим уравнение материального баланса для входной ячейки аппарата, указанной на схеме рис.3.4.1. Приход массы в эту ячейку складывается из прихода с входным потоком и прихода за счет обратного диффузионного потока. Расход складывается из конвективного уноса массы в последующие объемы аппарата.

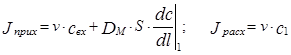
Для установившегося режима можно считать, что накопления массы во входном сечении аппарата не происходит и J_прих=J_расх. Устремим рассматриваемый входной объем к нулю, В этом случае с₁®с₀, 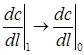и уравнение для граничного условия принимает вид:

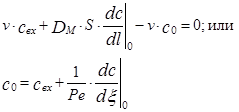(3.4.15)

Таким образом, из уравнения (3.4.15) следует, что концентрация вещества во входном сечении аппарата не равна концентрации во входном потоке, Она изменяется скачкообразно за счет действия обратного перемешивания.

Рассмотрим теперь вывод уравнения граничного условия для второй, выходной границы аппарата. Для этой границы мы также составим уравнение материального баланса при условии отсутствия накопления массы в выходном сечении аппарата.

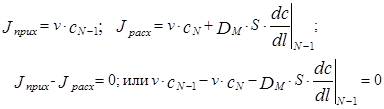
При Dl®0 c_N-1®c_N откуда следует, что

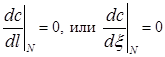(3.4.16)

Для определения постоянных интегрирования нужно подставить в уравнения (3.4.15) и (3.4.16) значения функции (3.4.12) при x=0 и x=1 и ее производных при этих же значениях аргумента. Для получения значения производной продифференцируем уравнение (3.4.12) по x. В итоге получим следующее уравнение:

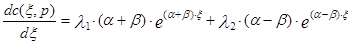(3.4.17)

Подставим выражение для производных и функций в уравнения граничных условий, получим следующие выражения для постоянных интегрирования:

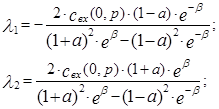(3.4.18)

где a=b¤a

Подставив найденные выражения для постоянных интегрирования в уравнение (3.4.12), найдем уравнение для зависимости концентрации от длины и переменной Лапласа в следующем виде:

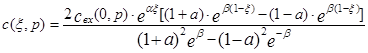(3.4.19)

Найдем передаточную функцию аппарата с конечными размерами. Для этого вычислим значение выходной концентрации, положив в уравнении (3.4.19) x=1.

В итоге получим:

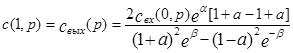(3.4.20)

откуда найдем передаточную функцию:

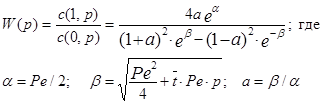(3.4.21)

Критерий Пекле Pe и коэффициент продольной диффузии D_M, являющиеся параметрами диффузионной модели определяют экспериментально с использованием экспериментов с трассерами. Методы определения параметров модели по экспериментальным данным мы рассмотрим ниже.

Рассмотрим решение уравнения диффузионной модели для аппарата бесконечно больших размеров. В таком аппарате возмущения не доходят до его границ. Поэтому можно считать, что концентрация на входе в аппарат равна концентрации во входном потоке, а концентрация на выходе равна нулю, при L®¥. Для этого случая граничные условия будут иметь вид:

с_вх(р)=с(0,р); с(1,р)®0, так как 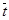®¥. Рассмотрим пределы для переменных a и b при ®¥.

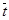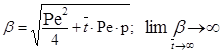, следовательно e^(a-b)®0, поэтому второй член выражения (3.4.12) l₂e^-(a-b)®0, тогда l₂¹0. Для того чтобы выполнялось второе граничное условие l₁e^(a+b)+l₂e^(a-b)=0, необходимо, чтобы член l₁e^(a+b) был равен нулю. Следовательно, l₁=0. Для нахождения второй постоянной интегрирования l₂ воспользуемся первым граничным условием при x=0, учитывая, что

с(x,р)=l₂e^(a-b)x

или при x=0 получим:

с(0,р)=с_вх(р)=l₂е^(a-b)×0=l₂

Окончательно будем иметь:

с(x,р)=с_вх(р) e^(a-b)x (3.4.22)

Концентрация на выходе из аппарата будет равна:

с_вых(1,р)=с_вх(р) e^(a-b) (3.4.23)

Откуда передаточная функция аппарата бесконечно больших размеров будет равна:

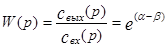(3.4.24)

Стационарный метод определения критерия Пекле.

Суть этого метода заключается в следующем. На некотором расстоянии от начала аппарата x=x₁ вводится трассер с постоянной скоростью.

Когда процесс станет установившимся, т.е. ¶c(x,t)/¶t=0, будет наблюдаться некоторое стационарное распределение концентрации трассера, Это распределение будет описываться стационарным уравнением диффузионной модели, которое получается из уравнения (3.49):

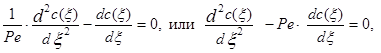(3.4.25

Решением уравнения (3.62) будет уравнение вида:

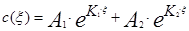(3.4.26)

где А₁ и А₂ постоянные интегрирования, которые находятся из граничных условий, соответствующих условиям проведения эксперимента, а К₁ и К₂ корни характеристического уравнения соответствующего исходному дифференциальному уравнению (3.4.25) характеристическое уравнение будет иметь вид: К²-РеК=0. Корни могут быть определены следующим образом:

К(К-Ре)=0. Тогда К₁=0, К₂=Ре. С учетом этого уравнение (3.4.26) примет вид:

с(x)=А₁+А₂×е^Ре×x (3.4.27)

Для нахождения А₁ воспользуемся первым граничным условием:

,

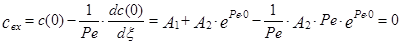Откуда следует, что А₁=0, так как концентрация трассера на входе в аппарат равна нулю. Для нахождения А₂ воспользуемся вторым граничным условием, а именно: при x=x₁ с(x)=с(x₁), следовательно, с(x₁)=А₂×e^Pe×x1, или

А₂=с(x₁)×е^-Реx1. Подставляя найденные значения постоянных интегрирования в (3.4.27), получим уравнение для описания стационарного профиля концентрации трассера:

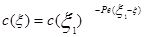(3.4.28)

Логарифмируя выражение (3.4.28), получим следующее уравнение:

ln(c(x))=ln(c(x₁)) – Ре(x₁-x) (3.4.29)