Нетрудно видеть, что предлагаемый в этой статье численный метод является весьма надежным и достаточно эффективным
ИТЕРАЦИОННЫЙ ЧИСЛЕННЫЙ МЕТОД ПОИСКА
ВСЕХ КОРНЕЙ АЛГЕБРАИЧЕСКИХ УРАПВНЕНИЙ
ВЫСОКИХ СТЕПЕНЕЙ.
В этой работе описан новый итерационный численный метод поиска всех корней алгебраических уравнений высоких степеней. Он основан на использовании принципа разложения многочлена на множители и идей сеточного метода , который успешно используется при решении сложных задач матемтической физики. Этот метод отличается от других методов , существующих в настоящее время для решения названной проблемы тем , что он практически одинаково надёжно и эффективно может быть использован для поиска всех видов корней : действительных или комплексных, близких или различных корней. Однако на практике этот метод целесообразно использовать для поиска корней уравнений достаточно высоких степеней , в особенности, для поиска всех собственных чисел матриц больших размерностей с действительными элементами. Метод проверен с помощью решения примера.
ВВЕДЕНИЕ.
При вычислении темпов роста членов динамических рядов данных в экономике, социологии, естественных науках, технике и при нахождении собственных значений матриц больших размерностей часто приходится находить корни уравнений с одним неизвестным очень высоких степеней
/ 1 ; 2 ; 3 /.
Кроме того, с целью повышения качества результатов анализа динамических рядов часто придется из множества действительных корней выбирать один наилучший корень. Собственные числа матриц больших размерностей могут быть также использованы в межотраслевом экономическом анализе.
Существующие в настоящее время методы решения такого вида задач могут оказаться на практике весьма неэффективными. Это особенно проявляется при поиске комплексных, а также близких или равных действительных корней. Для предлагаемого же в этой работе численного метода наличие комплексных, близких или даже равных действительных корней не снижает эффективности его применения для поиска всех корней алгебраических многочленов высоких степеней.
ОПИСАНИЕ ПРОБЛЕМЫ 
Далее, рассмотрим алгебраическое уравнение произвольной ( 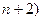 -й степени (
-й степени ( 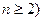 со старшим коэффициентом равным единице и при
со старшим коэффициентом равным единице и при 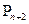
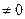 :
: 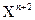 +
+ 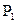
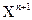 +…+
+…+ 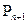
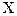 +
+ 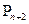 =0 (1) .
=0 (1) .  Если же
Если же 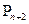 =0 , то степень рассматриваемого уравнения можно уменьшить. Причем, в новом уравнении самый младший коэффициент уже не будет равным нулю. Коэффициенты этого уравнения полагаем равными произвольным действительным числам. Известно, что это уравнение имеет (
=0 , то степень рассматриваемого уравнения можно уменьшить. Причем, в новом уравнении самый младший коэффициент уже не будет равным нулю. Коэффициенты этого уравнения полагаем равными произвольным действительным числам. Известно, что это уравнение имеет ( 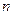 +2) неравных нулю корней, среди которых могут быть комплексно-сопряженные числа. Кроме того, известно также, что корни этого уравнения будут собственными значениями матрицы
+2) неравных нулю корней, среди которых могут быть комплексно-сопряженные числа. Кроме того, известно также, что корни этого уравнения будут собственными значениями матрицы 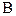
 ( и всех подобных ей матриц)/2 ;3/:
( и всех подобных ей матриц)/2 ;3/: 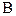 =
= 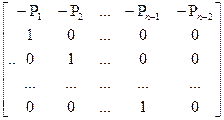 В результате применения , описанного ниже алгоритма , можно будет для целей анализа построить другую квадратную матрицу
В результате применения , описанного ниже алгоритма , можно будет для целей анализа построить другую квадратную матрицу  порядка (
порядка ( 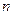 +2) . собственные значения которой будут полностью совпадать с собственными значениями матрицы
+2) . собственные значения которой будут полностью совпадать с собственными значениями матрицы 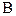 . Эта матрица
. Эта матрица 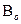 будет иметь весьма простую блочно-диагональную структуру :
будет иметь весьма простую блочно-диагональную структуру : 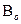 =
= 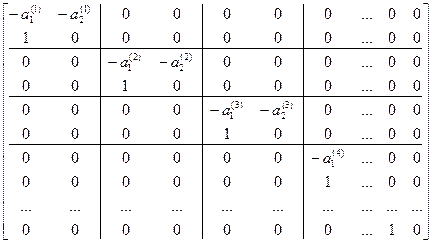 ;
; 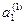 ,
, 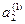 ,
, 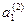 ,
, 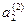 ,…. - коэффициенты соответствующих выделяемых многочленов. Нетрудно доказать, что
,…. - коэффициенты соответствующих выделяемых многочленов. Нетрудно доказать, что 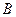 и
и 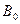
 подобные матрицы . В этой блочно-диагональной матрице полностью представлены только три блока, соответствующих трем выделяемым квадратным множителям рассматриваемого уравнения (1). Остальные диагональные блоки могут быть представлены в блочно-диагональной матрице
подобные матрицы . В этой блочно-диагональной матрице полностью представлены только три блока, соответствующих трем выделяемым квадратным множителям рассматриваемого уравнения (1). Остальные диагональные блоки могут быть представлены в блочно-диагональной матрице 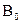 аналогично. Левую часть уравнения (1) можно записать так: f(
аналогично. Левую часть уравнения (1) можно записать так: f( 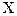 )=
)= 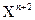 +
+ 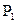
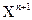 +…+
+…+ 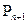
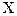 +
+ 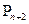 ; (2) Все корни уравнения (1) удовлетворяют условию : |
; (2) Все корни уравнения (1) удовлетворяют условию : | 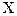 |
| 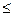 1+
1+ 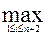 |
| 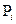 | ; (3).
| ; (3).
Обозначим 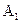 =1+
=1+ 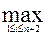 |
| 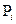 | . Таким образом, положительное число
| . Таким образом, положительное число 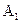 является верхней границей для модулей всех корней уравнения (1). Следует отметить тот факт , что эта граница часто будет весьма завышенной. В алгебре имеются различные способы для вычисления более точной оценки модулей корней многочленов. Например, в некоторых случаях замена переменной X по формуле Y=X/2 может позволить найти более точную оценку верхней границы модулей всех корней уравнения (1). Далее, если же все коэффициенты уравнения (1) строго положительны и все отношения
является верхней границей для модулей всех корней уравнения (1). Следует отметить тот факт , что эта граница часто будет весьма завышенной. В алгебре имеются различные способы для вычисления более точной оценки модулей корней многочленов. Например, в некоторых случаях замена переменной X по формуле Y=X/2 может позволить найти более точную оценку верхней границы модулей всех корней уравнения (1). Далее, если же все коэффициенты уравнения (1) строго положительны и все отношения 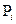 /
/ 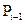 последующего коэффициента к предыдущему заключены между положительными числами
последующего коэффициента к предыдущему заключены между положительными числами 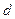 и
и 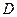 , то модули корней уравнения (1) будут удовлетворять условию:
, то модули корней уравнения (1) будут удовлетворять условию: 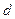
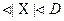 . Если среди коэффициентов
. Если среди коэффициентов 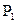 ,
, 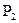 ,…,
,…, 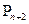 имеются отрицательные величины, то можно оценить верхнюю границу как для положительных, так и для отрицательных корней | 1 | . ( При использовании описанного ниже алгоритма не обязательно знать верхние границы модулей всех корней уравнения (1). Для использования этого алгоритма достаточно знать только верхнюю границу хотя бы двух каких-либо действительных корней или верхнюю границу одной какой-либо пары комплексно-сопряженных корней). Далее, пусть каким-либо способом получена оценка верхней границы всех корней уравнения (1). Обозначим это число символом
имеются отрицательные величины, то можно оценить верхнюю границу как для положительных, так и для отрицательных корней | 1 | . ( При использовании описанного ниже алгоритма не обязательно знать верхние границы модулей всех корней уравнения (1). Для использования этого алгоритма достаточно знать только верхнюю границу хотя бы двух каких-либо действительных корней или верхнюю границу одной какой-либо пары комплексно-сопряженных корней). Далее, пусть каким-либо способом получена оценка верхней границы всех корней уравнения (1). Обозначим это число символом 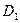 . Затем выполним следующее:
. Затем выполним следующее: 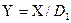 . В результате такой замены переменных получим вместо уравнения (1) новое уравнение (4):
. В результате такой замены переменных получим вместо уравнения (1) новое уравнение (4): 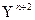 +
+ 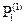
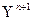 +…+
+…+ 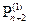 =0 , (4) где
=0 , (4) где 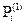 =
= 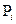 /
/ 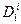 ,
, 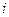 =1,2,…,
=1,2,…, 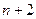 . Если
. Если 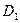 является верхней границей модулей всех корней уравнения (1) , то модули всех корней уравнения (4) не будут превосходить единицы. В противном же случае только модули некоторой пары корней не будут превосходить единицы. Далее , подробнее рассмотрим уравнение (4). Напишем следующее соотношение :
является верхней границей модулей всех корней уравнения (1) , то модули всех корней уравнения (4) не будут превосходить единицы. В противном же случае только модули некоторой пары корней не будут превосходить единицы. Далее , подробнее рассмотрим уравнение (4). Напишем следующее соотношение : 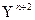 +
+ 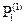
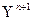 +… +
+… + 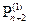 =(
=( 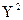 +
+ 
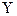 +
+  )(
)( 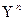 +
+ 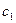
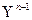 +…+
+…+ 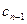
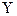 +
+ 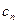 ) ; (5) То есть многочлен (
) ; (5) То есть многочлен ( 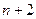 )-й степени представлен в виде произведения квадратного множителя и множителя
)-й степени представлен в виде произведения квадратного множителя и множителя 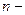 й степени. Очевидно, что
й степени. Очевидно, что  ,
,  ,
, 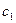 ,…,
,…, 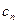 неизвестные действительные коэффициенты. В вычислительной математике существуют методы выделения аналогичных множителей. Однако в общем случае доказать их сходимость к искомым решениям практически невозможно | 2|. Здесь же предлагается численный метод , основанный на использовании идей сеточного метода/2/, успешно применяемого при поиске решений сложных задач математической физики. В данном случае предлагаемый численный метод является весьма надежным и всегда сходящимся. Далее, вышеописанные неизвестные коэффициенты
неизвестные действительные коэффициенты. В вычислительной математике существуют методы выделения аналогичных множителей. Однако в общем случае доказать их сходимость к искомым решениям практически невозможно | 2|. Здесь же предлагается численный метод , основанный на использовании идей сеточного метода/2/, успешно применяемого при поиске решений сложных задач математической физики. В данном случае предлагаемый численный метод является весьма надежным и всегда сходящимся. Далее, вышеописанные неизвестные коэффициенты  ,
,  ,
, 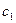 , …,
, …, 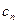 должны будут удовлетворять системе равенств(6):
должны будут удовлетворять системе равенств(6): 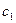 +
+  =
= 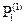
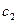 +
+ 
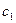 +
+  =
= 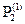
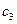 +
+ 
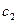 +
+ 
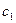 =
= 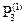 ……………………………. (6)
……………………………. (6) 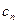 +
+ 
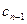 +
+ 
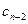 =
= 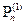

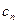 +
+ 
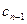 =
= 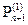

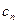 =
= 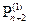 Ясно , что у этой системы уравнений существует решение. Неизвестными ее являются величины:
Ясно , что у этой системы уравнений существует решение. Неизвестными ее являются величины:  ,
,  ,
, 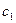 ,…,
,…, 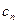 . Для каждой пары заданных значений величин
. Для каждой пары заданных значений величин  ,
,  , соответствующие им значения величин
, соответствующие им значения величин 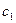 ,
, 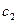 , …,
, …, 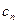 определяются по формулам системы (6) однозначно. И если значения величин
определяются по формулам системы (6) однозначно. И если значения величин  ,
,  определены точно, то все уравнения системы (6) будут удовлетворены. Нетрудно видеть , что если все корни уравнения (1) являются действительными и различными, то количество различных решений системы уравнений (6) будет равно:
определены точно, то все уравнения системы (6) будут удовлетворены. Нетрудно видеть , что если все корни уравнения (1) являются действительными и различными, то количество различных решений системы уравнений (6) будет равно: 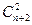 =(
=( 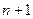 )(
)( 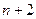 )/2. Когда же все корни уравнения (1) являются действительными и одинаковыми, то количество различных решений этой системы (6) будет равно единице. Во всех же остальных случаях количество различных решений этой системы (6) будет заключаться между 1 и
)/2. Когда же все корни уравнения (1) являются действительными и одинаковыми, то количество различных решений этой системы (6) будет равно единице. Во всех же остальных случаях количество различных решений этой системы (6) будет заключаться между 1 и 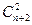 . На основе вышеизложенного можно построить алгоритм поиска хотя бы одного решения системы равенств (6). .
. На основе вышеизложенного можно построить алгоритм поиска хотя бы одного решения системы равенств (6). .
АЛГОРИТМ ПОИСКА РЕШЕНИЯ СИСТЕМЫ РАВЕНСТВ (6 ). Здесь будем исходить из того , что модули всех корней уравнения (4) не превышают единицы. Из формул Вьета следует, что величины  ,
,  могут принять следующие значения:
могут принять следующие значения:  =-(
=-( 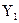 +
+ 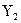 ) ;
) ;  =
= 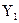
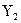 , где
, где 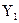 ,
, 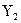 - какие-либо корни уравнения (4), которые могут быть даже одинаковыми действительными числами или парой комплексно-сопряженных чисел. Отсюда следует, что
- какие-либо корни уравнения (4), которые могут быть даже одинаковыми действительными числами или парой комплексно-сопряженных чисел. Отсюда следует, что  и
и  должны находиться в пределах: -2
должны находиться в пределах: -2 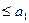
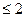 ; - 1
; - 1 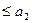
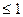 . (7)
. (7)
Рассмотрим , далее прямоугольную систему координат ( Рис 1). .


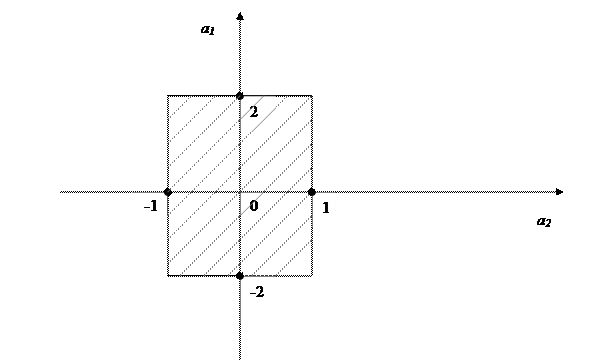
. Рис. 1. В заштрихованном прямоугольнике может находиться от одной до 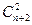 точек таких , что каждой из них будет соответствовать свое решение системы (6) :
точек таких , что каждой из них будет соответствовать свое решение системы (6) :  ,
,  ,
, 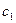 ,….,
,…., 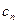 . Причем нас всякий раз будет интересовать только одно какое-либо из этих решений .( В данном случае все эти решения системы (6) являются равноценными). Теперь применим идею сеточного метода и опишем подробно шаги (части) вычислительного процесса (алгоритма). Для поиска искомой точки (
. Причем нас всякий раз будет интересовать только одно какое-либо из этих решений .( В данном случае все эти решения системы (6) являются равноценными). Теперь применим идею сеточного метода и опишем подробно шаги (части) вычислительного процесса (алгоритма). Для поиска искомой точки ( 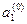 ,
, 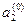 ) , которой соответствует решение системы (6) , проведем ( мысленно ) два семейства параллельных прямых:
) , которой соответствует решение системы (6) , проведем ( мысленно ) два семейства параллельных прямых:  =-2+
=-2+ 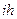 ;
; 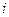 =0, 1, 2,….,
=0, 1, 2,…., 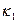 ;
; 
 =-1 +j
=-1 +j 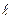 ; j=0,1,…,
; j=0,1,…, 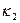 ;
; 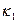 -наименьшее целое число, большее или равное дроби 4/
-наименьшее целое число, большее или равное дроби 4/ 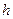 ;
; 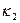 - наименьшее целое число , большее или равное дроби 2/
- наименьшее целое число , большее или равное дроби 2/ 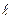 ;
; 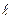 ,
, 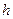 –шаги сетки. Точки пересечения этих прямых будут вершинами новых более мелких прямоугольников. Таким образом, заштрихованный прямоугольник ( Рис.1) будет (мысленно ) разделен на прямоугольники меньших размеров. Нетрудно видеть , что искомые точки (
–шаги сетки. Точки пересечения этих прямых будут вершинами новых более мелких прямоугольников. Таким образом, заштрихованный прямоугольник ( Рис.1) будет (мысленно ) разделен на прямоугольники меньших размеров. Нетрудно видеть , что искомые точки ( 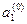 ,
, 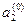 ) будут покрыты этими малыми прямоугольниками . Очевидно, что чем меньше шаги сетки
) будут покрыты этими малыми прямоугольниками . Очевидно, что чем меньше шаги сетки 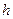 и
и 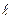 , тем точнее можно будет вычислить координаты искомых точек плоскости (
, тем точнее можно будет вычислить координаты искомых точек плоскости ( 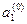 ,
, 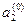 ), которым будут соответствовать решения системы (6). Отсюда несомненно следует сходимость предлагаемого вычислительного процесса поиска решения системы (6). Далее , шаги вычислительного процесса (алгоритма) поиска приближенного решения этой системы представим ниже. Для описания этих шагов дополнительно введем новые величины:
), которым будут соответствовать решения системы (6). Отсюда несомненно следует сходимость предлагаемого вычислительного процесса поиска решения системы (6). Далее , шаги вычислительного процесса (алгоритма) поиска приближенного решения этой системы представим ниже. Для описания этих шагов дополнительно введем новые величины: 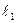 ,
, 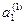 ,
, 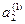 ,
, 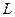 ,
, 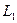
 ,
, 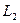 ,
, 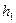 ,
, 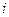 ,
, 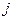 ,
, 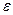 .
. 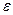 - сколь угодно малое положительное число , которое будет определяться требуемой точностью искомого решения системы (6) ; обычно
- сколь угодно малое положительное число , которое будет определяться требуемой точностью искомого решения системы (6) ; обычно 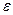 будет принимать значения не больше
будет принимать значения не больше 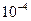 . Шаг 1. Положим , что
. Шаг 1. Положим , что 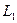 .=
.= 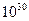 ( достаточно большому числу). Шаг 2. Положим , что
( достаточно большому числу). Шаг 2. Положим , что 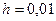 ,
, 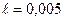 ; Шаг 3. Положим , что
; Шаг 3. Положим , что 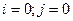 ;
; 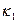 = наименьшему целому числу , которое больше или равно дроби 4/
= наименьшему целому числу , которое больше или равно дроби 4/ 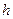 ;
; 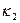 = наименьшему целому числу , которое больше или равно дроби 2/
= наименьшему целому числу , которое больше или равно дроби 2/ 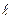 ; Шаг 4 Положим , что
; Шаг 4 Положим , что  = -2 +
= -2 + 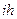 :
:
Шаг 5. Положим , что  =-1 +
=-1 + 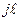 ; Шаг 6.На основе равенств системы (6) последовательно вычислим :
; Шаг 6.На основе равенств системы (6) последовательно вычислим : 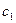 =
= 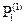 -
-  ;
; 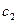 =
= 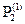 -
-  -
- 
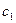 ;
; 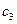 =
= 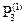 - (
- ( 
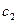 +
+ 
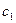 ); . ……………………………………………………………………….
); . ………………………………………………………………………. 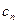 =
= 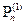 - (
- ( 
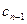 +
+ 
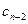 ). Затем переходим к выполнению следющего шага. Шаг 7.Вычислим значение величины
). Затем переходим к выполнению следющего шага. Шаг 7.Вычислим значение величины 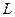 по формуле:
по формуле: 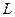 = |
= | 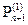 - (
- ( 
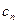 +
+ 
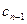 ) | + |
) | + | 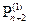 -
- 
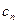 | . Эта величина
| . Эта величина 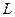 количественно характеризует степень согласованности двух последних уравнений системы (6) в процессе поиска решения этой системы. Очевидно , что для точного решения этой системы (6) величина
количественно характеризует степень согласованности двух последних уравнений системы (6) в процессе поиска решения этой системы. Очевидно , что для точного решения этой системы (6) величина 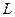 =0. Шаг 8. Если
=0. Шаг 8. Если 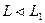 , то выполним шаг 9. В противном случае выполним шаг 10 . Шаг 9 . Положим
, то выполним шаг 9. В противном случае выполним шаг 10 . Шаг 9 . Положим 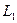 =
= 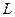 ;
; 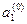 =
=  ;
; 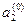 =
=  . Далее, выполним шаг 10.
. Далее, выполним шаг 10.
Шаг 10. Если 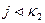 , то выполним шаг 11. В противном случае выполним шаг 12. Шаг 11. Увеличим значение величины
, то выполним шаг 11. В противном случае выполним шаг 12. Шаг 11. Увеличим значение величины 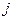 на единицу и переходим к выполнению шага 5. Шаг 12. Если
на единицу и переходим к выполнению шага 5. Шаг 12. Если 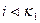 , то выполним шаг 13. В противном же случае выполним шаг 14. Шаг 13. Увеличим значение величины
, то выполним шаг 13. В противном же случае выполним шаг 14. Шаг 13. Увеличим значение величины 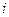 на 1, а величину
на 1, а величину 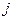 положим равной нулю и переходим к выполнению шага 4.
положим равной нулю и переходим к выполнению шага 4.
Шаг 14 . ( К моменту выполнения этого шага минимальное значение величины 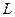 и соответствующие значения искомых величин
и соответствующие значения искомых величин 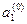 ,
, 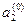 при данных значениях величин
при данных значениях величин 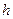 и
и 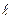
 будут вычислены. Полученные значения искомых величин
будут вычислены. Полученные значения искомых величин 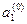 и
и 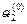 теперь можно будет значительно уточнить не меняя прежних значений величин
теперь можно будет значительно уточнить не меняя прежних значений величин 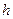 и
и 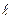 . ( Для этих целей можно , конечно, было бы использовать метод Хичкока |2| . Однако в данном случае целесообразнее применить более надежный метод уточнения значений величин
. ( Для этих целей можно , конечно, было бы использовать метод Хичкока |2| . Однако в данном случае целесообразнее применить более надежный метод уточнения значений величин 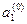 ,
, 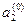 ) ; Положим теперь , что
) ; Положим теперь , что 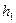 =
= 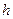 /100 ;
/100 ; 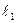 =
= 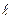 /100;
/100; 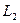 =
= 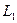 и переходим к выполнению шага 15.
и переходим к выполнению шага 15.
Шаг 15.Положим 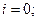
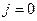 . Шаг 16. Положим
. Шаг 16. Положим  =
= 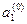 -
- 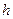 +
+ 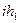 ; Шаг 17. Положим
; Шаг 17. Положим  =
= 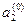 -
- 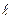 +
+ 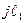 ; Шаг 18. На основе равенств системы (6) последовательно вычислим:
; Шаг 18. На основе равенств системы (6) последовательно вычислим: 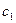 =
= 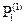 -
-  ;
; 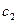 =
= 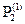 -
-  -
- 
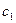 ;
; 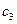 =
= 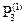 - (
- ( 
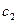 +
+ 
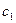 ) ; ……………………………………………………………………
) ; …………………………………………………………………… 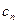 =
= 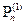 - (
- ( 
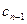 +
+ 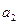
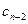 ); . Шаг 19. Вычислим значение величины
); . Шаг 19. Вычислим значение величины 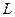 по формуле:
по формуле: 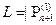 -
- 
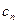 -
- 
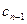 | + |
| + | 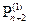 -
- 
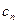 | . Шаг 20. Если
| . Шаг 20. Если 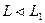 , то выполним шаг 21. В противном случае выполним шаг 22. Шаг 21. Положим
, то выполним шаг 21. В противном случае выполним шаг 22. Шаг 21. Положим 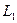 =
= 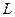 ;
; 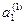 =
=  ;
; 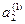 =
=  . Далее, выполним шаг 22.
. Далее, выполним шаг 22.
Шаг 22. Если 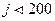 , то выполним шаг 23. В противном случае выполним шаг 24. Шаг 23. Увеличим значение переменной величины
, то выполним шаг 23. В противном случае выполним шаг 24. Шаг 23. Увеличим значение переменной величины 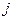 на единицу и выполним шаг 17. Шаг 24. Если же
на единицу и выполним шаг 17. Шаг 24. Если же 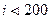 , то выполним шаг 25. В противном случае выполним шаг 26. Шаг 25. Увеличим значение величины
, то выполним шаг 25. В противном случае выполним шаг 26. Шаг 25. Увеличим значение величины 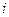 на единицу , а величину
на единицу , а величину 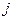 положим равной нулю и, далее, перейдем к выполнению шага 16.
положим равной нулю и, далее, перейдем к выполнению шага 16.
Шаг 26. Если же 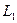
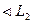 , то выполним шаг 27. В противном же случае выполним шаг 28. Шаг 27. Положим
, то выполним шаг 27. В противном же случае выполним шаг 28. Шаг 27. Положим 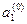 =
= 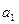
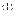 ;
; 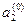 =
= 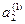 . Далее, выполним шаг 28.
. Далее, выполним шаг 28.
Шаг 28. Если же 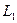
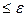 , то выполним шаг 30. В противном же случае выполним шаг 29. Шаг 29. В качестве новых значений величин
, то выполним шаг 30. В противном же случае выполним шаг 29. Шаг 29. В качестве новых значений величин 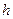 и
и 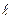 возьмем соответственно их предыдущие значения , умноженные на некоторую величину
возьмем соответственно их предыдущие значения , умноженные на некоторую величину 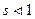 . ( В роли же величины
. ( В роли же величины 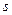 целесообразно брать числа:
целесообразно брать числа:
0,9 ; 0,8 ; 0,7; 0,6 ; 0,5. Причем, если требуется , чтобы шаги сетки 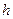 и
и 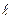 быстро уменьшались, то надо будет брать малые числа). Далее, переходим к выполнению шага 3. То есть начиная с этого шага вычислительный процесс повторится, но с новыми уменьшенными значениями шагов сетки
быстро уменьшались, то надо будет брать малые числа). Далее, переходим к выполнению шага 3. То есть начиная с этого шага вычислительный процесс повторится, но с новыми уменьшенными значениями шагов сетки 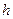 и
и 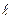 . При этом количество вычислений с новыми шагами сетки будет всякий раз возрастать. Шаг 30.Этот шаг означает завершение процесса нахождения таких значений величин:
. При этом количество вычислений с новыми шагами сетки будет всякий раз возрастать. Шаг 30.Этот шаг означает завершение процесса нахождения таких значений величин:  ,
,  ,
, 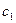 ,
, 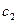 , …,
, …, 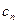 , при которых рассматриваемый многочлен :
, при которых рассматриваемый многочлен : 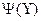 =
= 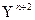 +
+ 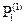
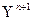 + …+
+ …+ 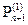
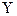 +
+ 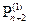 может быть представлен в виде произведения двух других многчленов :
может быть представлен в виде произведения двух других многчленов : 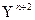 +
+ 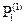
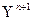 +…+
+…+ 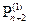 =(
=( 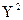 +
+ 
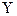 +
+  )(
)( 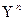 +
+ 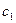
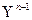 + …+
+ …+ 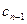
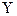 +
+ 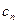 ) . Далее, если
) . Далее, если 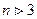 , то многочлен : (
, то многочлен : ( 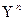 +
+ 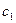
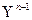 +…+
+…+ 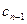
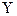 +
+ 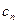 ) аналогично можно будет представить в виде произведения квадратного множителя и множителя (
) аналогично можно будет представить в виде произведения квадратного множителя и множителя ( 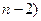 -й степени. Если же
-й степени. Если же 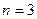 , то выделять квадратный множитель нецелесообразно, так как корни многочленов 3 –й степени находятся легко. ПРИМЕЧАНИЕ 1. В описанном выше алгоритме отмечалось, что модули всех корней уравнения (4) не превышают единицы. Однако нетрудно видеть, что если известно, что абсолютные значения каких-либо двух действительных корней уравнения (4) или модули какой-либо одной пары комплексно-сопряженных корней этого уравнения не превосходят единицы , то им будут соответствовать величины
, то выделять квадратный множитель нецелесообразно, так как корни многочленов 3 –й степени находятся легко. ПРИМЕЧАНИЕ 1. В описанном выше алгоритме отмечалось, что модули всех корней уравнения (4) не превышают единицы. Однако нетрудно видеть, что если известно, что абсолютные значения каких-либо двух действительных корней уравнения (4) или модули какой-либо одной пары комплексно-сопряженных корней этого уравнения не превосходят единицы , то им будут соответствовать величины  и
и  , удовлетворяющие ограничениям (7) . При этом модули остальных корней этого уравнения (4) могут превышать единицу. Однако даже в таких случаях применение вышеописанного алгоритма позволит из уравнения (4) выделить соответствующий квадратный множитель (
, удовлетворяющие ограничениям (7) . При этом модули остальных корней этого уравнения (4) могут превышать единицу. Однако даже в таких случаях применение вышеописанного алгоритма позволит из уравнения (4) выделить соответствующий квадратный множитель ( 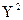 +
+ 
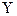 +
+  ).
).
ЧИСЛЕННЫЙ ПРИМЕР.
Пусть имеем уравнение 5-й степени с одним неизвестным: 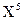 +
+ 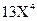 +
+ 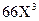 +
+ 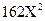 +
+ 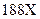 + 80 =0 . (8) Здесь , очевидно,
+ 80 =0 . (8) Здесь , очевидно, 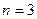 . Далее :
. Далее : 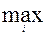 |
| 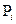 | =188 ;
| =188 ; 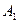 =1+188 =189
=1+188 =189
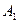 - верхняя граница для модулей всех корней уравнения (8). Однако таким способом вычисленная верхняя граница модулей корней уравнения обычно является весьма завышенной. Поэтому попытаемся получить более низкую оценку верхней границы для корней уравнения (8). Так как все коэффициенты уравнения строго положительные, то имеет смысл вычислить все отношения последующего коэффициента к предыдущему : ( 13/1 ; 66/13 ; 162/66 ; 188/162 ; 80/188 ) . Очевидно , что верхней границей модулей всех корней уравнения (8) будет число 13. Поэтому выполним замену переменных по формуле:
- верхняя граница для модулей всех корней уравнения (8). Однако таким способом вычисленная верхняя граница модулей корней уравнения обычно является весьма завышенной. Поэтому попытаемся получить более низкую оценку верхней границы для корней уравнения (8). Так как все коэффициенты уравнения строго положительные, то имеет смысл вычислить все отношения последующего коэффициента к предыдущему : ( 13/1 ; 66/13 ; 162/66 ; 188/162 ; 80/188 ) . Очевидно , что верхней границей модулей всех корней уравнения (8) будет число 13. Поэтому выполним замену переменных по формуле: 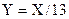 . В результате получим новое уравнение:
. В результате получим новое уравнение: 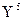 +
+ 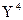 + (66/
+ (66/  )
) 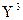 + (162/
+ (162/ 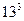 )
) 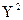 + ( 188/
+ ( 188/ 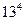 )
) 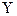 + 80/
+ 80/ 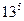 =0 . или
=0 . или 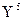 +
+ 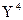 + 0,3905
+ 0,3905 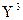 + 0,07374
+ 0,07374 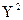 + 0,006582
+ 0,006582 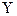 +0,0002155 =0. (9)
+0,0002155 =0. (9)
