Модель множественной регрессии

Средняя ошибка аппроксимации

Фактическое значение результативного признака y отличается от теоретических значений 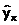, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим, и лучше качество модели.

Величина отклонений фактических и расчетных значений результативного признака 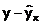по каждому наблюдению представляет собой ошибку аппроксимации.

Поскольку 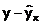может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Отклонения 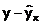можно рассматривать как абсолютную ошибку аппроксимации, а 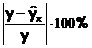- как относительную ошибку аппроксимации.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации: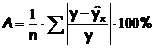

Возможно и иное определение средней ошибки аппроксимации: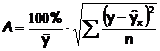

Если А£10-12%, то можно говорить о хорошем качестве модели.

Коэффициент эластичности

Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительного изменения экономического фактора, от которого он зависит при неизменных остальных влияющих на него факторов.

Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.

Формула для расчета коэффициента эластичности имеет вид: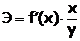

Обычно рассчитывается средний коэффициент эластичности: .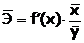

Формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:

Вид функции, y	Первая производная, y'	Средний коэффициент эластичности,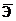
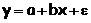	b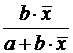
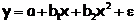	b1+2b2x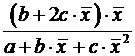

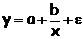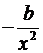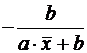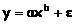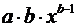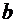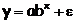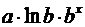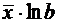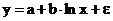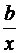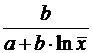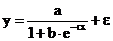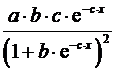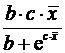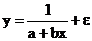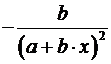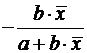Несмотря на широкое применения в эконометрике коэффициентов эластичности, возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.

Модель множественной регрессии.

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

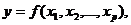
где 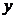- зависимая переменная (результативный признак);

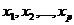- независимые переменные (факторы).

Линейная модель множественной регрессии имеет вид:

Yi = α0 + α1xi1 + α2xi2 + ... + α mxim + εi (4.1)

Коэффициент регрессии αj показывает, на какую величину в среднем изменится результативный признак Y, если переменную xj увеличить на единицу измерения, т.е. αj является нормативным коэффициентом. Обычно предполагается, что случайная величина εi имеет нормальный закон распределения с математическим ожиданием равным нулю и с дисперсией σ2.

Анализ уравнения (4.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (4.2):

Y = X α + ε (4.2)

где Y — вектор зависимой переменной размерности n×1, представляющий собой n наблюдений значений yj,

X — матрица n наблюдений независимых переменных Х1, Х2, Х3, ..., Хm, размерность матрицы X равнаn×(m+1);

α — подлежащий оцениванию вектор неизвестных параметров размерности (m+1) ×1;

ε — вектор случайных отклонений (возмущений) размерности n×1.

Таким образом,

Уравнение (4.1) содержит значения неизвестных параметров α0, α1, α2, ..., αm. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид:

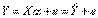, (4.3)

где α — вектор оценок параметров; е — вектор «оцененных» отклонений регрессии, остатки регрессии ε = Y - Xα; 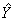— оценка значений Y, равная Ха.

Для построения уравнения множественной регрессии чаще используются следующие функции:

линейная –

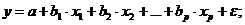
степенная –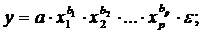

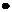экспонента –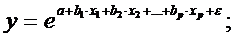

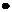гипербола - .

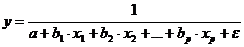Можно использовать и другие функции, приводимые к линейному виду.