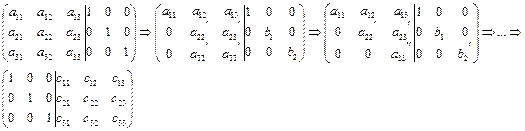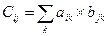Отношения эквивалентности

Определим некоторые важные свойства бинарных отношений и рассмотрим бинарные отношения, которые обладают тремя из этих свойств и часто встречаются в математике. Такое бинарное отношение называется эквивалентностью.

СВОЙСТВА:

1. 1.1 Пусть 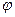- бинарное отношение, 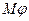- область его задания, тогда 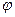называется рефлексивным, если 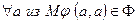, граф таких отношений имеет вид петли при каждой вершине

1.2 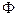называется антирефлексивным, если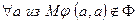

2. 2.1 Отношение может быть симметричным, если

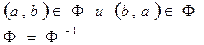(изображается любым графом)

Антисимметричным, если 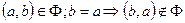(изображается ориентированным графом)

3. 3.1 Транзитивным. Отношение называется транзитивным, если 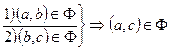(изображается транзитивным графом – все вершины пересекаются)

Если для бинарного отношения 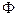соблюдается три условия: рефлексивность, симметричность и транзитивность, то такое отношение называется эквивалентностью.

МАТРИЦЫ И ГРАФЫ

Понятие матрицы. Виды матриц. Свойства матриц. Линейные операции над матрицами. Единичные матрицы. Обратные матрицы

Матрицей называется прямоугольная таблица чисел размером 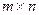, где m – число строк, а n – число столбцов.

Если m=n – матрица называется квадратной.

Если m-1 – матрица-строка.

Если n=1 – матрица-столбец.

Все числа, входящие в матрицу называются ее элемен­тами. Если все элементы состоят их нулей, то это нулевая матрица, она играет роль нуля в матричном исчислении.

Рассмотрим некоторые линейные операции над матрицами:

1. Сумма

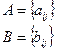
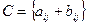
Исходя из определения можно складывать и вычитать матрицы только одного размера.

2. Произведение матрицы на число называется матрица, где каждый элемент матрицы умножается на это число.

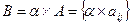
3. Матрица умножается на матрицу по правилу строка на столбец

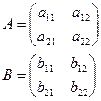
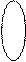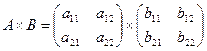
такое правило не годится для всех матриц, а именно, количество строк во второй матрице должно равняться количеству столбцов в первой матрице.

Квадратные матрицы перемножаются только одного размера.

4. Единичной матрицей называется квадратная матрица любого размера, где по главной диагонали стоят единицы, а все остальные элементы равны нулю.

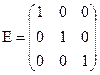, играет роль единицы в матричном исчислении.

Если такую матрицу умножить на другую матрицу (при возможности умножения) даст исходную матрицу.

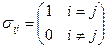
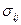- дельта Кронекера

5. Обратной матрицей 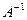называется матрица, которая 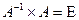, заметим, что Е – квадратная, соответственно 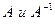тоже квадратные.

6. 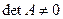(определитель), если 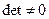, то обратная матрица существует, если 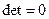, то матрица называется вырожденная.

Нахождение обратной матрицы

1. Метод присоединенной матрицы

1.

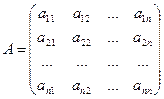
2.

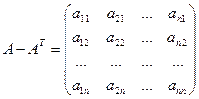
3.

3.1 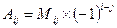(взаимная)

3.2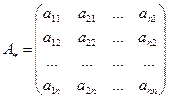

4.

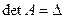
5.

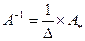
2. Метод элементарных преобразований