Силовые линии и эквипотенциали

Для наглядного представления векторных полей используют картину силовых линий. Силовая линия есть воображаемая математическая кривая в пространстве, направление касательной к которой в каждой точке, через которую она проходит, совпадает с направлением вектора поля в той же точке (рис. 1.17).

Условие параллельности вектора E→ и касательной можно записать

в виде равенства нулю векторного произведения E→ и элемента дуги dr→ силовой линии: [dr→,E→] = 0. (9.1)

Векторное уравнение (9.1) есть система трёх скалярных уравнений, но только два из них независимы. В декартовой системе его обычно записывают следующих образом:

dx Ex = dy Ey = dz Ez .

За положительное направление силовой линий принимают направление самого вектора поля E→. При таком соглашении можно сказать, что электрические силовые линии начинаются от положительных зарядов и оканчиваются на отрицательных. На рис. 1.18 изображены силовые линии положительного и отрицательного зарядов.

Рис. 1.18:

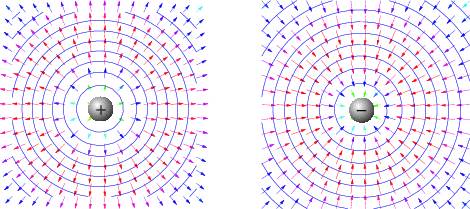
Эквипотенциалью называют поверхность, на которой постоянна величина электрического потенциала ϕ. В поле точечного заряда, как показано на рис. 1.18, эквипотенциальными являются сферические поверхности с центров в месте расположения заряда; это видно из уравнения ϕ = q∕r = const.

Анализируя геометрию электрических силовых линий и эквипотенциальных поверхностей, можно указать ряд общих свойств геометрии электростатического поля.

Во-первых, силовые линии начинаются на зарядах. Они либо уходят на бесконечность, либо заканчиваются на других зарядах, как на рис. 1.19.

Рис. 1.19:

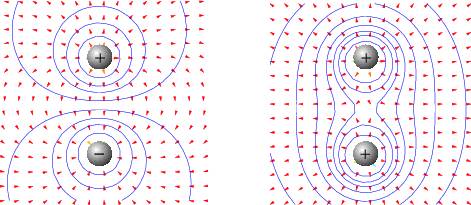
Во-вторых, в потенциальном поле силовые линии не могут быть замкнуты. В противном случае можно было бы указать такой замкнутый контур, что работа электрического поля при перемещении заряда по этому контуру не равна нулю.

В-третьих, силовые линии пересекают любую эквипотенциаль по нормали к ней. Действительно, электрическое поле всюду направлено в сторону скорейшего уменьшения потенциала, а на эквипотенциальной поверхности потенциал постоянен по определению

Рис. 1.20:

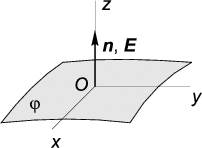
И наконец, силовые линии нигде не пересекаются за исключением точек, где E→ = 0. Пересечение

силовых линий означает, что поле в точке пересечения есть неоднозначная функция координат, а вектор E→ не имеет определенного направления. Единственным вектором, который обладает таким свойством, является нулевой вектор.

Метод силовых линий, конечно, применим для графического представления любых векторных полей. Так, в главе ?? мы встретим понятие магнитных силовых линий. Однако геометрия магнитного поля совершенно отлична от геометрии электрического поля.

Рис. 1.21:

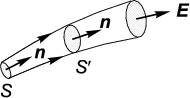
Представление о силовых линиях тесно связано с понятием силовой трубки. Возьмем какой-либо произвольный замкнутый контур L и через каждую точку его проведём электрическую силовую линию (рис. 1.21). Эти линии и образуют силовую трубку. Рассмотрим произвольное сечение трубки поверхностью S. Положительную нормаль проведём в ту же сторону, в какую направлены силовые линии. Пусть N — поток вектора E→ через сечение S. Нетрудно видеть, что если внутри трубки нет электрических зарядов, то поток N остаётся одним и тем же по всей длине трубки. Для доказательства нужно взять другое поперечное сечение S′. По теореме Гаусса, поток электрического поля через замкнутую поверхность, ограниченную боковой поверхностью трубки и сечениями S, S′, равен нулю, так как внутри силовой трубки нет электрических зарядов. Поток через боковую поверхность равен нулю, так как вектор E→ касается этой поверхности. Следовательно, поток через сечение S′ численно равен N, но противоположен по знаку. Внешняя нормаль к замкнутой поверхности на этом сечении направлена противоположно n→. Если же направить нормаль в ту же сторону, то потоки через сечения S и S′ совпадут и повеличине, и по знаку. В частности, если трубка бесконечно тонкая, а сечения S и S′ нормальны к ней, то

ES = E′S′.

Получается полная аналогия с течением несжимаемой жидкости. В тех местах, где трубка тоньше, поле E→ сильнее. В тех местах, где она шире, поле E→ сильнее. Следовательно, по густоте силовых линий можно судить о напряженности электрического поля.

До изобретения компьютеров для экспериментального воспроизведения силовых линий брали стеклянный сосуд с плоским дном и наливали в него жидкость, не проводящую электрически ток, например, касторовое масло или глицерин. В жидкости равномерно размешивали истертые в порошок кристаллики гипса, асбеста или какие-либо другие продолговатые частицы. В жидкость погружали металлические электроды. При соединении с источниками электричества, электроды возбуждали электрическое поле. В этом поле частицы электризуются и, притягиваясь друг к другу разноименно наэлектризованными концами, располагаются в виде цепочек вдоль силовых линий. Картина силовых линий искажается течениями жидкости, вызываемыми силами, действующими на неё в неоднородном электрическом поле.

Лучшие результаты получаются по методу, применявшемуся Робертом В. Полем (1884–1976). На стеклянную пластинку наклеиваются электроды из станиоля, между которыми создается электрическое напряжение. Затем на пластинку насыпают, слегка постукивая по ней, продолговатые частички, например, кристаллики гипса. Они располагаются по ней вдоль силовых линий.

Уравнение Пуассона.

Произвольное векторное поле E→(r→) характеризуется тремя скалярными функциями Ej(r→), где j пробегает значения x, y, z (если говорить о декартовой системе координат). Поэтому одного уравнения (6.2), вообще говоря, недостаточно, чтобы найти электрическое поле. Однако электростатическое поле потенциально. Это накладывает столь сильное ограничение, что все три компоненты E→ можно выразить через одну скалярную функцию — электрические потенциал ϕ. Подставляя

E→ = −gradϕ.

в уравнение

divE→ = 4πρ

получаем уравнение Пуассона Δϕ = −4πρ. (10.1)

где дифференциальный оператор Δ = divgrad называется оператором Лапласа, или лапласианом. Уравнение Пауссона играет столь важную роль в электростатике, что его часто называют основным уравнением электростатики. В декартовой системе координат оно записывается следующим образом: ∂2ϕ ∂x2 + ∂2ϕ ∂y2 + ∂2ϕ ∂z2 = −4πρ. (10.2)

В произвольной криволинейной системе координат для вычисления оператора Δ необходимо исходить из инвариантных определений дивергенции и градиента (см. 6 и 8).

Уравнение Пуассона относится к классу дифференциальных уравнений в частных производных. Иногда специальным выбором системы координат его удается свести к обыкновенному дифференциальному уравнению. Это случается, если в такой специальной системе координат плотность заряда и потенциал зависят от одной координаты.