Сейсмическая томография на временных задержках
Время пробега луча — функция скорости 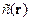 и геометрии лучевойтраектории. Можно ставить задачу реконструкции скоростного закона
и геометрии лучевойтраектории. Можно ставить задачу реконструкции скоростного закона 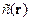 , по множеству измерений времени на поверхности Земли:
, по множеству измерений времени на поверхности Земли:
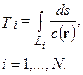 (2.28)
(2.28)
Особенностью этой задачи служит то, что неизвестная скоростная функция 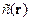 в неявном виде присутствует и в определении лучевой траектории Si. Это приводит к существенной нелинейности задачи реконструкции
в неявном виде присутствует и в определении лучевой траектории Si. Это приводит к существенной нелинейности задачи реконструкции 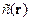 . В значительном числе случаев известно нулевое приближение
. В значительном числе случаев известно нулевое приближение 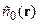 к скоростному закону
к скоростному закону 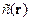 и следует уточнить поправки к нулевому приближению так, чтобы наблюдаемые времена прихода и рассчитанные были близки друг к другу. Исходя из скоростного закона
и следует уточнить поправки к нулевому приближению так, чтобы наблюдаемые времена прихода и рассчитанные были близки друг к другу. Исходя из скоростного закона 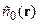 , можно рассчитать траектории лучей
, можно рассчитать траектории лучей 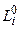 в модели нулевого приближения. Обозначим время, предсказываемое начальной моделью,
в модели нулевого приближения. Обозначим время, предсказываемое начальной моделью, 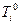 :
:
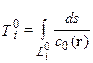
Здесь 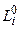 — траектория луча в начальной модели. Определим время задержки как
— траектория луча в начальной модели. Определим время задержки как
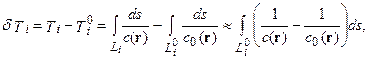
Или:
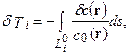 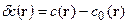 | (2.29) |
Задача (29) представляет собой задачу сейсмической томографии. Измерены временные задержки. Задана начальная модель, следует реконструировать поправочные слагаемые к модели начального приближения. Это уравнение можно формально записать в виде отображения с помощью линейного оператора  пространства функций поправок
пространства функций поправок 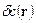 в пространство временных задержек
в пространство временных задержек 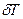 :
:
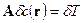 | (2.30) |
Это операторная запись соотношения (30). Уравнение (29) практически повторяет уже приведенные уравнения в 2.2 для задач ультразвуковой и акустической томографии. Однако спецификой сейсмических задач служит неполнота данных – невозможность получить временные задержки по всем необходимым траекториям. Это делает невозможным использование методов интегральных преобразований для обращения уравнения (29). Основными оказываются алгебраические методы. Их суть состоит в следующем.
Разобьем область  , в которой происходит процесс распространения волн, на элементарные ячейки
, в которой происходит процесс распространения волн, на элементарные ячейки 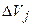 , которые пронумеруем индексом j. Сделаем это таким образом, чтобы в пределах каждого из
, которые пронумеруем индексом j. Сделаем это таким образом, чтобы в пределах каждого из 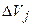 функция
функция 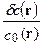 принимала постоянное значение равное
принимала постоянное значение равное 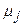 . Обозначим длину луча, имеющего нумерацию
. Обозначим длину луча, имеющего нумерацию 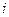 , проходящего через объем
, проходящего через объем 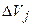 через
через 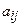 . Тогда конечномерная модель задачи характеризуется системой уравнений:
. Тогда конечномерная модель задачи характеризуется системой уравнений:
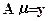 , где
, где 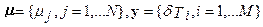 . Особенностью матрицы A и, как следствие, свойства задачи восстановления модели распределения медленности состоит в том, что она:
. Особенностью матрицы A и, как следствие, свойства задачи восстановления модели распределения медленности состоит в том, что она:
1) имеет большую размерность: M= 500 – 1500, N= 300- 1000;
2) сильно разряжена и имеет ленточную структуру;
3) плохо обусловлена что проявляется в практической неединственности решения и его сильной зависимости от осцилляций во входных данных.
Эти особенности требуют развития специальных приемов вычисления.
