Кинематика механизмов с низшими кинематическими парами

В этом разделе изучаются методы исследования кинематики механизмов с низшими парами (или рычажных механизмов).

Задачи исследования; исходные данные; методы исследования

Задачи исследования

1)Определение положений звеньев механизма и определение траекторий отдельных его точек.

2)Определение линейных скоростей точек механизма и угловых скоростей его звеньев.

3)Определение линейных ускорений точек механизма и угловых ускорений его звеньев.

Исходные данные

Для решения задач кинематики необходимо иметь

1)Кинематическую схему механизма и все кинематические размеры его звеньев.

2)Закон движения входного (ведущего) звена.

Методы исследования

1)Аналитический.

2)Графо-аналитический (метод планов положений,скоростей и ускорений).

3)Метод графического дифференцирования.

4)Экспериментальный.

Аналитический метод

Метод заключается в определении математических выражений, 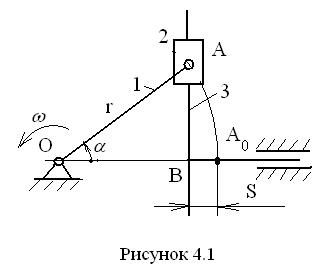описывающих функциональную связь между входными и выходными параметрами механизма. Для этого служат различные приёмы и методы, такие как метод векторных контуров, который образуется заменой кинематических размеров звеньев векторами, с последующим проецированием этого контура на оси системы координат и получением на этой основе соответствующих уравнений, описывающих кинематику данного механизма. Этой же цели служит метод разбиения схемы механизма на прямо- или косоугольные треугольники, решая которые, получают необходимые математические выражения.

Для составления некоторого первоначального представления о методе рассмотрим кинематику синусного механизма (рис. 4.1). Механизм состоит из кривошипа 1, вращающегося вокруг неподвижной точки О, конец А которого образует вращательную кинематическую пару с ползуном 2. Ползун движется по вертикальному элементу ведомого звена 3, которое движется вдоль неподвижных гоизонтальных направляющих. На первом этапе определяется зависимость перемещения S ведомого звена от угла α₁ поворота ведущего кривошипа 1. Из рис. 4.1 видно, что

.

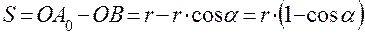Дифференцируя по 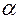в первый раз, получаем аналог скорости ведомого звена:

,

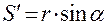дифференцируя во второй раз, получаем аналог ускорения ведомого звена

.

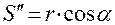З а м е ч а н и е . Следует обратить внимание на то, что зависимость 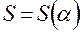, отражающая закон преобразования движения в механизме, называется функцией положения механизма. Её первая производная по 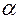, как отмечено выше, называется аналогом скорости (или передаточной функцией скорости), вторая производная – аналогом ускорения (или передаточной функцией ускорения). Для получения скорости и ускорения в функцию положения необходимо ввести время, для этого вместо 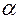необходимо подставить 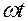и выполнить дифференцирование по времени 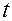. Попутно обнаруживается и связь между кинематическими функциями и их аналогами.

4.3. Метод планов положений, скоростей и ускорений