Программа исследований
Разработка схемы преобразователя кода
Произвести синтез многовыходной комбинационной схемы для четырех или пяти (в зависимости от варианта задания) переключательных функций четырех переменных (табл. 1.). Привести минимизированные функции y0, y1, y2, y3, y4 к элементному базису И–НЕ либо ИЛИ–НЕ. Выбор элементной базы определяется критерием минимальных аппаратных затрат в расчете на количество корпусов микросхем малого уровня интеграции (МИС). Считать, что в одном корпусе ИС размещается:

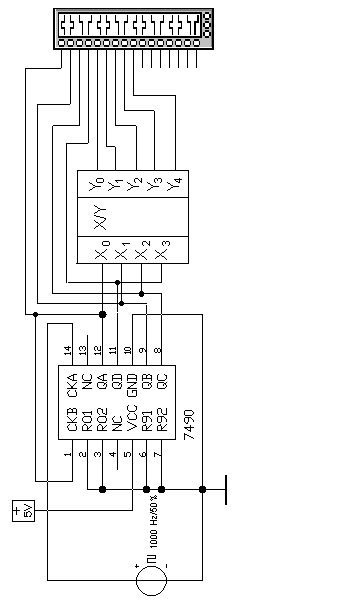
Варианты заданий
Таблица 1
| № кодовой комбинации | Входной код | 1. Код “2-4-2-1” | 2. Код “3-3-2-1” | |||||||||
| X3 | X2 | X1 | X0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 3. Дополнение до 10 | 4. Дополнение до 16 | 5. Код “2 из 5” | ||||||||||
| Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y4 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 6. Код Джонсона | 7. Код Грея 1 | 8. Код Грея 2 | ||||||||||
| Y4 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 9. Код “3 из 5” | 10. Код Грея 3 | 11. Код Грея 4 | ||||||||||
| Y4 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 12. Код Грея 5 | 13. Код Грея 6 | 14. Код Грея 7 | |||||||||
| Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 15. Код Грея 8 | 16. Код Грея 9 | 17. Код Грея 10 | |||||||||
| Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 18. Код Грея 11 | 19. Код Грея 12 | 20. Код Грея 13 | |||||||||
| Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
Продолжение табл. 1
| № код. комб. | 21. Код с избытком 6 | 22. Код “4-3-2-1” | 23. Код “5-2-1-1” | |||||||||
| Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | Y3 | Y2 | Y1 | Y0 | |
6 инверторов;
4 двухвходовых элемента;
3 трехвходовых элемента;
2 четырехвходовых элемента;
1 восьмивходовый элемент.
Ниже приведен пример синтеза переключательной функции.
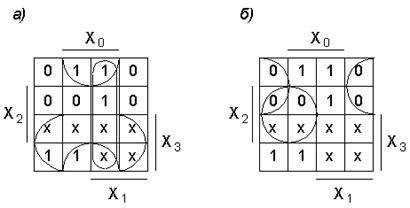
Рис. 2. Диаграммы Вейча функции четырех переменных
На рис. 2, а показано объединение ячеек, содержащих единицы, которое позволяет получить минимальную дизъюнктивную форму синтезируемой функции, приводящую к реализации в базисе И–НЕ:
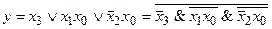 .
.
Для реализации схемы требуется два инвертора (1 / 3 ИС), два двухвходовых элемента (1 / 2 ИС) и один трехвходовый элемент (1 / 3 ИС), то есть всего 7 / 6 корпуса ИС.
На рис. 2, б показано объединение ячеек, содержащих нули, которое позволяет получить минимальную дизъюнктивную форму для инверсии синтезируемой функции, удобную для реализации в базисе ИЛИ–НЕ:
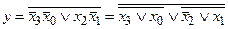 .
.
Для реализации функции в такой форме требуется один инвертор (1 / 6 ИС) и три двухвходовых элемента (3 / 4 ИС), то есть всего 11 / 12 корпуса ИС. В этом примере более экономична реализация заданной функции в базисе ИЛИ–НЕ.
