Закон распределения дискретной случайной величины. Многоугольник распределения
Введение
Настоящее учебно-методическое пособие написано авторами на основе многолетнего опыта преподавания теории вероятностей в общем курсе “Высшая математика” на химическом факультете ННГУ.
Учебно-методическое пособие содержит краткие теоретические сведения, такие как понятие случайной величины, законы распределения случайных величин, функция распределения, числовые характеристики случайных величин, а также важнейшие законы распределения случайных величин.
Пособие включает в себя подробно решенные типовые задачи и достаточно большое количество разнообразных задач с ответами для самостоятельной работы.
Данное учебно-методическое пособие носит учебный характер. Его цель – помочь студентам лучше усвоить общие теоретические положения и развить навыки в их применении при решении конкретных задач.
Понятие случайной величины. Закон распределения случайной величины
Одним из важнейших понятий теории вероятностей (наряду со случайным событием и вероятностью) является понятие случайной величины.
Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, причем заранее, до опыта, неизвестно, какое именно.
Случайные величины обозначаются заглавными буквами латинского алфавита –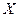 
, 
, 
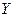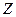, …, а принимаемые ими значения - соответствующими малыми буквами 
.
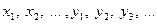Случайная величина, принимающая конечное или счетное множество значений: называется дискретной или прерывной случайной величиной.
Непрерывной случайной величиной называется случайная величина, бесконечное несчетное множество возможных значений которой есть некоторый промежуток (конечный или бесконечный) числовой оси. (Строгое определение непрерывной случайной величины будет дано ниже).
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины. Многоугольник распределения
Закон распределения может иметь разные формы. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.
Простейшей формой задания закона распределения дискретной случайной величины X является таблица (матрица), в которой в порядке возрастания перечислены все возможные значения случайной величины и соответствующие их вероятности, т.е.
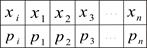
или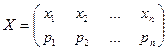 
, где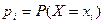 
; 
.
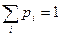Такая таблица называется рядом распределениядискретной случайной величины X.
Графическое изображение ряда распределения (см. рис.1) называется многоугольником (или полигоном) распределения.
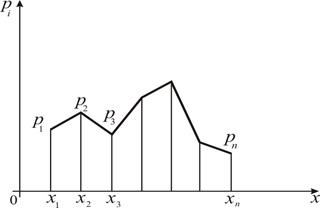
Рис. 1