На курсовуЮ(ой) работу(проект)
ЗАДАНИЕ
НА КУРСОВУЮ РАБОТУ
ПО ДИСЦИПЛИНЕ МДК 01.02
«Математический аппарат для построения компьютерных сетей»
Студенту группы: ЯРКС-211( 12-КС-11)
Тема: «Применение математического аппарата для анализа компьютерной сети предприятия»
Содержание курсовой работы:
1. Описание предприятия
2. Схема сети
3. Использование теории графов для анализа участков сети
4. Использование задачи линейного программирования
Дата выдачи задания 17.01.2013
Срок сдачи курсовой работы 6.05.2013
Руководитель __ Кипцевич И.А
Председатель ЦК_______________________________ Кипцевич И.А
Зав. отделением ________________________________ Полянская М.В
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Ярославский филиал
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Московский государственный университет путей сообщения»
ОТЗЫВ
На курсовуЮ(ой) работу(проект)
По дисциплине «_____________________________»
Студента группы ________________________________
__________________
Тема _____________
__________________
__________________
1. Объем курсовой(го) работы(проекта):
а) количество страниц пояснительной записки _________
б) количество листов графической части _________
2. Оценка содержания курсовой(го) работы (проекта), ее(его) положительные стороны и недостатки, выводы, рекомендации к защите:
__________________
______
Рекомендуемая оценка ________ «___________________».
Рецензент _______________ ________________
(подпись) (расшифровка подписи)
«_____»_____________20___ г.
СОДЕРЖАНИЕ
Введение
1 Описание предприятия
1.2 Сервер предприятия
1.3 Программное обеспечение
2 Схема сети предприятия
3 Использование теории графов для анализа участков сети
3.1 Теория графов
3.2 Алгоритм Краскала
3.3 Участок сети согласно алгоритму Краскала
3.4 Транспортная сеть
3.5 Транспортная сеть с максимальным потоком в сети.
4 Линейное программирование
4.1 Использование задачи линейного программирования
Заключение
Список используемых источников
ВВЕДЕНИЕ
В данной курсовой работе нам предстоит описать предприятие и проанализировать его сеть при помощи математического аппарата. Первые работы по современному сетевому анализу относятся к 1941-47 годам. В данных работах были заложены основные принципы применения сетевого анализа. В дальнейших работах теория сетевого анализа и графов развивалась и дополнялось и в настоящее время она относится наряду с теорией СМО к основному математическому аппарату который в большинстве случаев используется для анализа ИВС. Необходимость использования теории графов было обусловлено необходимостью решения задач маршрутизации в сети, а так же невозможностью на базе моделей СМО решить задачи распределения трафика т.к. модели СМО анализа ИВС используют «аппроксимацию независимостью Клейнрока». В последнее время наметилась тенденция применения теории графов совместно с теорией нечетких множеств и теорией вероятности, что обусловлено невозможностью сведения большого класса задач к линейному программированию. Как результат образование математического аппарата стохастических сетей позволяющий получить более адекватные модели процессов в ИВС, переходы в которых не могут быть описаны детерминированными величинами. Применение теории нечетких множеств позволило еще в большей степени расширить применение математического аппарата графов за счет создания комплексных моделей в которых веса ребер имеют детерминированное значение с заданной вероятностью, что является более общем случаем стохастических сетей. В настоящее время, теория графов является одном из основных математических аппаратов применяемых для анализа поведения ИВС на сетевом уровне ЭМВОС. Высока методологическая проработанность, простота, наглядность – основные качества моделей построенных на базе математического аппарата теории графов. Вместе с тем у моделей теории графов есть ряд существенных недостатков. Первоначально построенная на математике линейного программирования теория графов оперирует заведомо детерминированными связями и стационарными потоками. Во-первых, это приводит к невозможности создания моделей сети с нестационарными потоками. Во-вторых, введение в теорию графов элементов вероятности хотя и позволило описать ряд статистических процессов, но в тоже время нельзя распространить результаты такого моделирования на широкий класс стохастических процессов в сетях. Однако, справедливо заметим, что такие попытки предпринимаются в рамках комплексных моделей построенных с применением теории графов и теории нечетких множеств в этом случае нечетким множеством задают: множество кратчайших переходов, множество связных ребер, множество весов и др.
1 ОПИСАНИЕ ПРЕДПРИЯТИЯ
Компьютер Сервис – компьютерный сервис по ремонту, обслуживанию и продаже компьютеров, комплектующих, ноутбуков и периферийного оборудования. Самый важный этап начинается с тщательного изучения представленной работы опытными программистами -конструкторами компании. С учетом всех факторов, эксплуатационных нагрузок и требований заказчика производятся необходимые расчеты, подбираются материалы и оборудование, проектируется объект и подготавливаются все необходимые документы. После чего проект согласовывается с заказчиком. Сборка и установка осуществляется только профессиональными техниками и программистами, прошедшими специальное обучение. Квалифицированные и опытные специалисты, качественные материалы, тщательно составленный проект - на этом этапе это три самых главных коэффициента работы. Компания применяет самое современное техническое оборудование и расходные материалы. Слаженность команды программистов и техников, качественная подготовка материалов, компонентов и проекта выливаются в высокую скорость выполнения работ. Производственную практику проходил в Компьютер Сервисе. ООО «Компьютер Сервис» специализируется на модернизации, поставке компьютерного оборудования, кассовое оборудование, системы, торговое оборудование, расходные материалы, ремонт, обслуживание, компьютеры, периферийные устройства, ремонт компьютеров, техническое обслуживание, программное обеспечение. В отделе находятся 6 человек, 4 техника, 1 системный администратор, и директор Компьютер Сервиса. В здании компании находятся 1 сервер, 15 рабочих станций, 1 ноутбук, 4 маршрутизатора, так же имеется wifi роутер. Основной операционной системой была Windows 7 на сервере установлен Windows Server 2008 R2.
Наш сервис существует с 2005г. и является динамично развивающимся и постоянно расширяющим свой профиль деятельности.
· Продажа компьютерной и офисной техники
· Ремонт и обслуживание компьютеров, ноутбуков, комплектующих и периферийного оборудования
· Купля/продажа поддержанной компьютерной техники
· Создание, продвижение и поддержка сайтов
В рамках компьютерного обслуживания мы предоставляем следующие услуги:
Оперативная компьютерная помощь с выездом мастера в офис или на дом. Специалист в кратчайшие сроки выедет к клиенту, оценит сложившуюся ситуацию, определит план дальнейших действий или приступит к ремонту, настройке компьютера, периферийного оборудования или ЛВС непосредственно на месте .
Установка компьютерных комплектующих, периферийных устройств. В рамках данной услуги возможна установка любых компьютерных комплектующих или периферийных устройств как сервисного центра, так и клиента. Вы также можете получить бесплатную консультацию об оптимальной конфигурации компьютера или о модернизации старого у наших специалистов. После установки наш специалист обязательно осуществит тонкую настройку компьютерных комплектующих, периферийных устройств, т.к. нормальная работа компьютера невозможна без его предварительной настройки, как для повышения быстродействия, так и для настройки под потребности клиента. Актуальную информацию о ценах на компьютерные комплектующие, а также периферийное оборудование Вы можете получить у нашего диспетчера.
Установка операционной системы а также необходимого и дополнительного программного обеспечения. Операционная система - основная программная среда компьютера, обеспечивающая взаимоотношение всех установленных поверх неё программ, драйверов и имеющая свои тонкости установки и настройки, справиться с которыми под силу только специалисту. Кроме операционной системы по предварительному заказу специалист может осуществить доставку и установку практически любого программного обеспечения.
Настройка интернет подключения. Большинство людей уже не представляет своей жизни без сети интернет, без её безграничных возможностей для общения и обмена информацией. Профессии многих людей непосредственно связаны с интернет. В ходе данной услуги осуществляется: подключение и настройка соответствующего оборудования, установка и настройка необходимого программного обеспечения для работы в сети интернет, пробное тестовое соединение с сетью.
Установка антивируса, антивирусная проверка и чистка компьютера. Распространение огромного количества вредоносных программ в сети интернет, всплывающих рекламных окон и др. делают невозможной стабильную и безопасную работу компьютера в сети интернет без использования комплекса программных продуктов, противодействующих нежелательному проникновению на компьютер пользователя. Специалист нашего сервиса установит надёжную антивирусную систему, а также настроит её под индивидуальные требования клиента.
Восстановление информации. Различные сбои в работе компьютера в результате сбоев электросети или неправильного выключения компьютера, а также случайное удаление или форматирование могут привести к потере важной информации. Специалисты нашего сервиса имеют опыт восстановления потерянных данные после удаления, форматирования, изменения файловой системы даже в самых трудных случаях с любых источников информации.
Настройка локальной сети. Локальные сети позволяют наиболее просто и удобно для Вас решить задачи оперативного обмена информацией между участниками сети, создания единой базы данных, общего доступа к периферийному оборудованию многое другое. Специалисты сервисного центра «Компьютер Сервис» в соответствии вашими требованиями и Вашими техническими возможностями подберут Вам наиболее удобный вариант, помогут с выбором оборудования, настройкой и последующим обслуживанием сети. Возможна установка системы ограничения трафика, шифрования информации и др.
Модернизация компьютера. Стремительное развитие компьютерной индустрии, технологий приводят не только к естественному физическому износу, но и к моральному устареванию компьютерной техники, а соответственно к необходимости замены их на более современные, более мощные и производительные компоненты.
Сборка компьютеров под заказ. Исходя из разнообразных индивидуальных потребностей существует необходимость именно индивидуального подхода к сборке компьютеров. Универсальных конфигураций практически не существует. Кто-то предпочитает использовать компьютер, как исключительно рабочую лошадку, а кому-то нужен центр развлечений, способный на многое.
1.2 Сервер предприятия
Intel 4U P4304BTLSHCNR (LGA1155, C204, 1xPCI-E, SVGA, SATA RAID, 4xHotSwapSAS / SATA, 2xGbLAN, 4DDR-III, 365W)
Рисунок 1 - Корпус
CPU Intel Xeon E3-1240V2 3.4 ГГц / 4core / 1+8Мб / 69 Вт / 5 ГТ / с LGA1155
Рисунок 2 - Процессор
TITAN < TTC-NC25TZ / PW(RB)> Cooler (4пин, 1155 / 1366 / 775 / 754-AM2 / AM3 / FM1, 13.8-35дБ, 1500-3500об / мин, Al+тепл.трубки)
Рисунок 3 - Куллер
Kingston ValueRAM < KVR16E11 / 8> DDR-III DIMM 8Gb < PC3-12800> CL11 ECC
Рисунок 4 - Оперативная память
HDD 1 Tb SATA-II 300 Western Digital RE4 < WD1003FBYX> 3.5" 7200rpm 64Mb
Рисунок 5 - Жесткий диск
DVD RAM & DVD±R / RW & CDRW Optiarc AD-7280S < Black> SATA (OEM)
Рисунок 6 - Привод
1.3 Программное обеспечение
На Сервере установлен Windows Server 2008 R2. Вы регулярно сталкиваетесь с проблемами растущих потребностей бизнеса. Организации требуется круглосуточная работоспособность, а необходимый уровень безопасности и соответствия требованиям еще никогда не был так высок. Эти потребности совмещаются с ежедневными проблемами по поддержанию постоянно разрастающегося парка серверов, ресурсов и бюджета. Windows Server 2008 R2 с пакетом обновлений SP1 создан для того, чтобы помочь вам улучшить контроль, работоспособность и гибкость вашего центра обработки данных и инфраструктуры настольных компьютеров, и одновременно с этим сократить затраты на рутинные операции.
Основные преимущества:
1. Дополнительные возможности виртуализации
2. Повышенная масштабируемость и надежность
3. Улучшенная виртуализация рабочих столов
4. Улучшенное управление серверами
5. Интеграция с Windows 7
В последней версии технология виртуализации получила значительные улучшения. Использование встроенных мощных средств виртуализации поможет Вам изменить способ предоставления ИТ-услуг пользователям в Вашей организации и дать возможность заложить фундамент для частной облачной инфраструктуры.
Gene6 FTP Server - один из лучших FTP-серверов с расширенным администрированием и высоким уровнем безопасности передаваемых данных.
Kaspersky Crystal— это основное решение для безопасной работы. Продукт обеспечивает постоянную защиту от современных вирусных угроз. Защита от вирусов и шпионских программ в режиме реального времени, проверка веб-сайтов и программ на наличие вредоносного кода.
Adobe Reader - является мировым стандартом для совместной работы с электронными документами. Это единственная программа для просмотра файлов PDF, которая позволяет открывать все PDF-документы и работать с ними в интерактивном режиме.
Adobe Photoshop - растровый графический редактор, разработанный и распространяемый фирмой Adobe Systems.
Microsoft Office - Офисный пакет приложений, созданных корпорацией Microsoft для операционных систем Microsoft Windows и Apple Mac OS X. В состав этого пакета входит программное обеспечение для работы с различными типами документов: текстами, электронными таблицами, базами данных и др.
2 СХЕМА СЕТИ
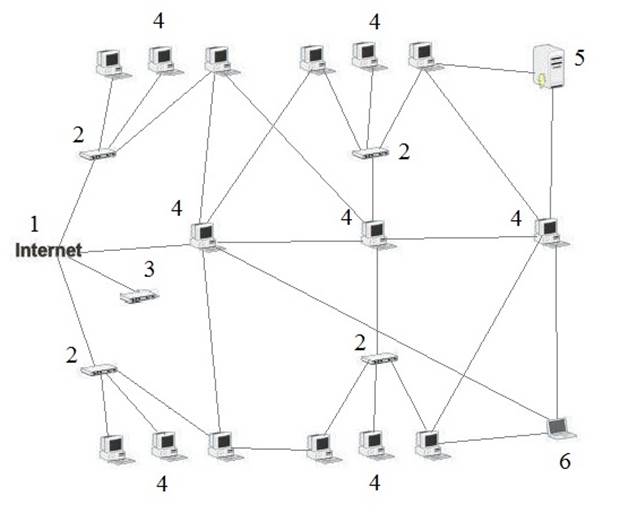
Рисунок 7 - Схема сети предприятия
Таблица 1 - Обозначения
| Номер | Обозначения |
| Интернет | |
| Маршрутизаторы | |
| WiFi Роутер | |
| Рабочие станции | |
| Сервер | |
| Ноутбук |
3 ИСПОЛЬЗОВАНИЕ ТЕОРИИ ГРАФОВ ДЛЯ АНАЛИЗА УЧАСТА СЕТИ.
3.1 Теория графов
Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин, соединённых рёбрами. В строгом определении графом называется такая пара множеств G=(V,E), где V есть подмножество любого счётного множества, а E — подмножество V×V. Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут. При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. где внутри фигуры раскрывается смысл вершины. Если между вершинами существует ребро, то соответствующие точки соединяются отрезком или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра. Различают планарные и не планарные графы. Планарный граф — это граф, который можно изобразить на рисунке без пересечения рёбер (простейшие — треугольник или пара связанных вершин), иначе — не планарный. В том случае, если граф не содержит циклов, его принято называть «деревом». Важные виды деревьев в теории графов — бинарные деревья, где каждая вершина имеет одно входящее ребро и ровно два выходящих, или является конечной — не имеющей выходящих рёбер. Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.
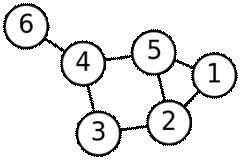
Рисунок 8 - Граф с шестью вершинами и семью рёбрами
Одной из первых работ по Г. т. можно считать работу Л. Эйлера (1736), относящуюся к решению головоломок и математических развлекательных задач. Первые глубокие результаты были получены в 1-й половине 20 в. в связи с решением задач построения электрических цепей и подсчёта химических веществ с различными типами молекулярных соединений. Однако широкое развитие Г. т. получила лишь с 50-х гг. в связи со становлением кибернетики и развитием вычислительной техники, когда Г. т. существенно обогатилась и новым материалом, и новыми подходами и когда началось систематическое изучение графов с разных точек зрения (структурной, информационной и т. д.). Именно в это время формулировались проблематика и методы Г. т. Г. т. находит применение в теории программирования и при построении вычислительных машин, в изучении физических, химических и технологических процессов, в решении задач планирования, в лингвистических и социологических исследованиях и т. д. Г. т. имеет тесные связи как с классическими, так и с новыми разделами математики; это — топология, алгебра, комбинаторный анализ, теория чисел, теория минимизации булевских функций. Г. т. включает большое число разнообразных задач. Одни из них группируются в отдельные направления, другие стоят более изолированно. Среди сложившихся разделов Г. т. следует отметить задачи, относящиеся к анализу графов, определению различных характеристик их строения, например выяснение связности графа: можно ли из любой вершины попасть в любую; подсчёт графов или их частей, обладающих заданными свойствами, например подсчёт количества деревьев с заданным числом рёбер (дерево — неориентированный граф без циклов); решение транспортных задач, связанных с перевозками грузов по сети. Решен ряд задач по синтезу графов с заданными свойствами, например построение графа с заданными степенями вершин (степень вершины — число выходящих из неё рёбер). Имеет прикладное и теоретическое значение задача о выяснении возможности расположения графа на плоскости без самопересечений его рёбер (т. е. является ли данный граф плоским), задача о разбиении графа на минимальное число плоских графов. Для некоторых задач Г. т. (выше были приведены далеко не все) были разработаны методы их решения. Среди них: метод Пойя перечисления и подсчёта графов с заданными свойствами, теорема и алгоритм форда — фалкерсона для решения транспортной задачи, "венгерский" алгоритм решения задачи о назначениях и т. д. Почти все задачи теории конечных графов (практически интересны именно графы с конечным числом вершин) могут быть решены путём перебора большого числа вариантов (т. н. полный перебор), поэтому для них требуется построение эффективных алгоритмов и использование быстродействующих вычислительных машин. Такими задачами являются: задача о раскраске вершин графа, задача об определении идентичности двух графов, коммивояжёра задача. Есть задачи, требующие принципиального ответа, например задача о раскраске плоских графов, задача о восстановлении графа по его подграфам.
3.2 Алгоритм Краскала
Алгоритм Краскала— алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году. Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса.
Алгоритм Краскала может строить дерево одновременно для нескольких компонент связности, которые в процессе решения объединяются в одно связанное дерево. Полный граф задается списком ребер. Перед работой список ребер сортируется по возрастанию длины. На каждом шаге просматривается список ребер, начиная с ребра, следующего за вошедшим в решение на предыдущем шаге, и к строящемуся поддереву присоединяют то ребро, которое не образует цикла с ребрами, уже включенными в решение. Алгоритм состоит из следующей последовательности действий:
Создается список ребер R, содержащий длину ребра, номер исходной вершины ребра (i), номер конечной вершины ребра (j), признак включения данного ребра в дерево. Данный список упорядочивается в порядке возрастания длин ребер. Просматривается список R и выбирается из него ребро с максимальной длиной, еще не включенное в результирующее дерево и не образующее цикла с уже построенными ребрами. Если все вершины включены в дерево и количество ребер на единицу меньше количества вершин, то алгоритм свою работу закончил. В противном случае осуществляется возврат к пункту 3.
Или в терминах теории графов:
Дан граф с n вершинами; длины ребер заданы матрицей. Найти остовное дерево максимальной длины. В задаче Прима-Краскала, которая не кажется особенно простой, жадный алгоритм дает точное оптимальное решение. Как известно (это легко доказать по индукции), дерево с n вершинами имеет n-1 ребер. Оказывается, каждое ребро нужно выбирать жадно (лишь бы не возникали циклы). То есть n-1 раз выбирать самое короткое ребро из еще не выбранное ребро при условии, что оно не образует цикла с уже выбранными. А как следить, чтобы новое ребро не образовывало цикла со старыми? Сделать это просто. До построения дерева окрасим каждую вершину i в отличный от других цвет i. При выборе очередного ребра, например (i, j), где i и j имеют разные цвета, вершина j и все, окрашенные в ее цвет (т.е. ранее с ней соединенные) перекрашиваются в цвет i. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора n-1 ребер все вершины получают один цвет. Докажем, что описанный алгоритм получает в точности максимальное решение. Для доказательства нам понадобится очень простое утверждение: Если к дереву добавить ребро, то в дереве появится цикл, содержащий это ребро. Действительно, пусть добавлено ребро (u, v) - “добавлено” означает, что ребро - новое, что раньше его в дереве не было. Поскольку дерево является связанным графом, то существует цепь C (u, …, v) из нескольких ребер, соединяющая вершины u и v. Добавление ребра (u, v) замыкает цепь, превращая ее в цикл.
Теорема. Алгоритм Прима-Краскала получает максимальное остовное дерево.
Доказательство. Результатом работы алгоритма является набор из n-1 ребер. Они не образуют цикла, ибо на каждом из n-1 шагов соединялись вершины разного цвета, т.е. ранее не связанные. Этот граф связный, потому что после проведения 1-го ребра осталось n-1 разных цветов, …, после проведения (n-1) - го ребра остался один цвет, т.е. одна компонента связности. Итак, полученный набор ребер образует связный граф без циклов, содержащий n-1 ребер и n вершин. Следовательно, граф есть остовное дерево. Осталось доказать, что оно имеет минимальную длину. Пусть {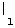 
, 
, …, 
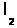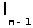} ребра остовного дерева в том порядке как их выбирал алгоритм, т.е. 
≥ 
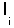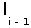. Предположим для простоты доказательства, что все ребра сети имеют разную длину, т.е.
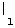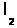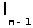> >…> (1)
Если полученное дерево не максимально, то существует другое дерево, заданное набором из n-1 ребер {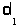 
, 
, …, 
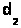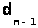}, такое что сумма длин 
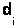больше суммы длин 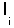. С точностью до обозначений
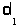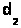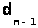> >…> (2)
Может быть 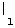= 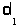, 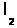= 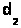и т.д., но так как деревья разные, то в последовательностях (1) и (2) найдется место, где ребра отличаются. Пусть самое левое такое место - k, так, что 
№ 
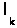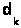. Поскольку 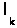выбиралось по алгоритму самым большим из не образующих цикла с ребрами , , …, 
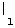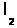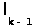, то 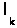> 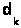. Теперь добавим к дереву (2) ребро 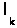. В нем появится цикл, содержащий ребро 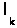и, может быть, какие-то (или все) ребра 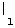, , 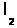…, , 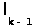но они сами не образуют цикла, поэтому в цикле будет обязательно ребро d из набора 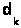, …, , 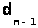причем d> 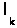. Выбросим из полученного графа с одним циклом ребро d. Мы снова получим дерево, но оно будет на d- 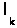короче минимального, что невозможно. Полученное противоречие доказывает теорему для сети со всеми разными ребрами.
Алгоритм состоит из следующей последовательности действий:
- Создается список ребер E, содержащий длину ребра, номер исходной вершины ребра (i), номер конечной вершины ребра (j), признак включения данного ребра в дерево.
- Данный список упорядочивается в порядке возрастания длин ребер.
- Просматривается список E и выбирается из него ребро с максимальной длиной, еще не включенное в результирующее дерево и не образующее цикла с уже построенными ребрами.
- Если все вершины включены в дерево и количество ребер на единицу меньше количества вершин, то алгоритм свою работу закончил. В противном случае осуществляется возврат к пункту 3.
3.3 Участок сети согласно алгоритму Краскала.
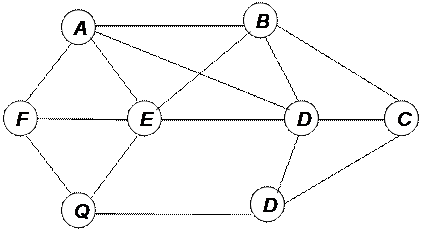
Выбираем участок из нашей компьютерной сети предприятия.
1
2 3 4 4
5 7
1 4
3 1
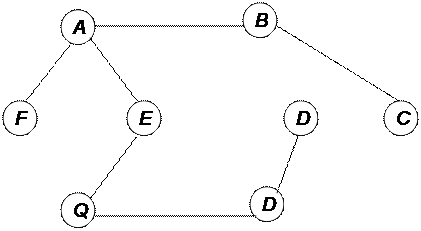
Рисунок 9 - Участок сети
С помощью алгоритма Краскала получаем следующее основное дерево минимального потока сети.
 |
2 2
Рисунок 10 - Применение алгоритма Краскала
Последовательность выбираемых рёбер: (A,B),(D,H),(E,Q),(Q,H),(A,F), (A,E),(B,C)
Поток:1+2+1+1+2+2+3+3=14
3.4 Транспортная сеть.
В теории графов транспортная сеть - это ориентированный граф G = (V,E), в котором каждое реброимеет неотрицательную пропускную способность. Целочисленная транспортная сеть - транспортная сеть, все пропускные способности ребер которой - целые числа.
Транспортная сеть - ориентированный граф G = (V,E), в котором:
- Каждому ребруприписана неотрицательная пропускная способность и поток f(u,v). Если,то
- Выделены две вершины: источникsi и стокdj, такие, что любая другая вершина сети лежит на пути из siвdj.
- Поток - функция со следующими свойствами для любых вершинu и v:
- Ограничение пропускной способности. Поток не может превысить пропускную способность:
- Антисимметричность. Поток изu вv должен быть противоположным потоку из vв u:
- Сохранение потока: для всех , кроме источника и стока.
Величиной потоканазывается сумма потоков из источника.
Разрез - разбиение множества всех вершин V на два подмножества, S и D, таких что, пропускная способность разреза (S,D) - суммапропускных способностей всех рёбер из S в D .
Поток через разрез (S,D) - сумма всех потоков из S в D . Он не превышает пропускную способность разреза, поскольку .
Транспортная сеть обладает следующим рядом свойств:
- Поток через любой разрез равен сумме потоков из источника.
- Сумма потоков из источника равна сумме потоков в сток.
- Максимальный поток положителен тогда и только тогда, когда существует путь из источника в сток, проходящий по рёбрам с положительной пропускной способностью.
- Поток максимален тогда и только тогда, когда нет увеличивающего пути в остаточной сети.
- Величина максимального потока равна пропускной способности минимального разреза.
Транспортные сети удобно моделировать при помощи графов. Зарождение теории графов в XVIII веке было связано с математическими головоломками, и довольно долго на учение о графах смотрели как на «несерьезную» тему, значение которой целиком связывали с играми и развлечениями. Первая работа по теории графов, принадлежащая швейцарскому математику Л. Эйлеру, появилась в 1736 году. Уже в XIX столетии графы использовались при построении схем электрических цепей и молекулярных схем. В настоящее время существуют главы чистой математики, например, теория математических отношений, в которых теория графов служит естественным аппаратом. С другой стороны, эта теория находит многочисленные применения в разнообразных практических вопросах, в том числе в задачах планирования и управления производством. Теория графов очень популярна при решении транспортных задач, хотя только этой областью применения она, конечно не исчерпывается.
3.5 Транспортная сеть с максимальным потоком в сети.
Выберем часть сети из нашей сети предприятия которая будет являться транспортной и найдём максимальный поток.
I). Насыщение потока
1.Пронумеруем вершины сети
2.Насыщаем пути из 0 в 9:
1) 0 2 1 2 4 2 7 2 9 условно разрываем насыщенное ребро
1 2 4 (показано штриховкой на рисунке 5)
2) 0 4 1 2 3 2 6 2 9 условно разрываем насыщенное ребро
0 4 1
3) 0 2 2 2 5 2 8 2 9 условно разрываем ребро 2 2 5
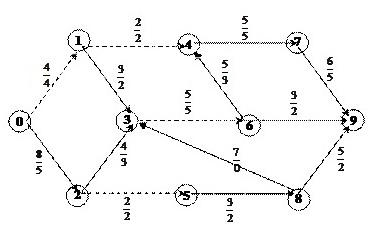
Рисунок 11 - Часть транспортной сети
4) 0 3 2 3 3 3 6 3 4 3 7 3 8 условно разрываем
 | | | | | |
насыщенное ребро 3 3 6
Сеть насыщенна и "разорвана". Поток текущий по сети: 5+2+2=9
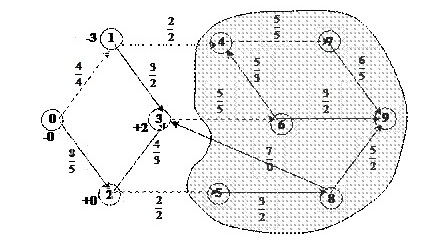
Рисунок 12 - Насыщенная и "разорванная" сеть
II) Ищем максимальный поток в сети.
Пометим все возможные вершины сети.
1) Вершину 0 пометим -0
2) Непомеченные вершины, смежные с вершиной 0, - это вершины 1 и 2.
Вершину 1 из вершины 0 пометить нельзя, так как ребро 0 4 1 насыщенно.
Пометим вершину 2 меткой +0, поскольку ребро 0 3 2 не насыщенно.