Элементы теории графов

Наука, занимающаяся графическими представлениями, - геометрия из-за своей наглядности получила широкое распространение уже в древности. Так, задолго до жившего в VI в. до н.э. Пифагора была известна теорема, которая позже стало носить его имя. Наглядность геометрии широко используется в наше время, в том числе при анализе больших технических и организационных систем, в которых используют теорию графов.

Граф– совокупность вершин и ребер – универсальное средство наглядного представления достаточно разнообразных задач.

Разнообразные сочетания различных ребер и вершин представляют многообразие возможных графов и их применения. Граф, в котором вершины – прямоугольники и направления ребер не заданы, описывают блок-схему (или структуру) организационно-технической системы. Граф-дерево – многоуровневая иерархическая система, в которой все вершины распределены по нескольким уровням. Граф с дугами, изображающими связь между вершинами, - сеть.

Сетями представляют различные задачи, в которых исследуют перемещение или выполнение работ во времени. Сеть характеризуется структурой и параметрами дуг. Структура (топология) сети показывает, какие вершины связаны между собой, и направление связывающих их дуг.

Каждую вершину сети нумеруют порядковым номером. Начальную 1 вершину в описании движения потоков называют источником, конечную – стоком. В общем случае дугу обозначают i-j, где i – номер вершины, из которой исходит дуга; j – номер вершины, в которую входит дуга. Каждая дуга имеет свою характеристику: t_ij – продолжительность движения по дуге i-j; c_ij – стоимость перемещения; d_ij – пропускная способность дуги и т.д.

Зная топологию сети и ее параметры, можно решать самые разнообразные, часто встречающиеся задачи оптимизации.

Задача коммивояжера

Пример. Пусть имеются 5 пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт (рис.1). Известно время перевозки из пункта i в пункт j (табл.1).

Рисунок 1.

Таблица 1.

Из пункта i	В пункт j

Требуется найти такой маршрут, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда, чтобы его продолжительность была минимальной.

Решение. Для решения этой задачи необходимо составить математическую модель. Введем обозначения: i и j – номера пунктов выезда и въезда; t_ij – время переезда из пункта i в пункт j. Из таблицы 1 видно, что t_ij в общем случае может быть не равно времени переезда в обратном направлении t_ij 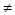t_ji (например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевые переменные:

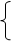1, если из пункта i торговец переедет в пункт j

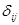= 0, если не поедет.

Составим модель. Из пункта 1 можно выехать в любой из пунктов 2 или 5, или 3, или 4, или остаться в пункте 1. Но при этом можно выехать только в одном единственном направлении. Это условие можно записать так:

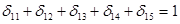, или ,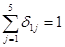

или для произвольного i-ого пункта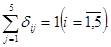

Эти зависимости обеспечивают выполнение условия, что из каждого пункта выезд производится только один раз и только в одном направлении.

Условие въезда в пункт 1 аналогично условию выезда из пункта 1. Требование минимальной продолжительности маршрута запишется в виде целевой функции:

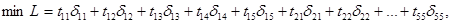
где t_ij берутся из исходной таблицы 1, а 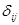- искомые переменные.

Тогда всю задачу можно сформулировать:

,

,

, (*)

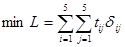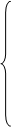
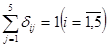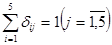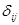= [0;1] .

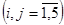В результате решения системы (*) получим (рис.2) следующие значения 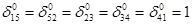, остальные 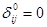; min L = 10+8+10+20+14=62.

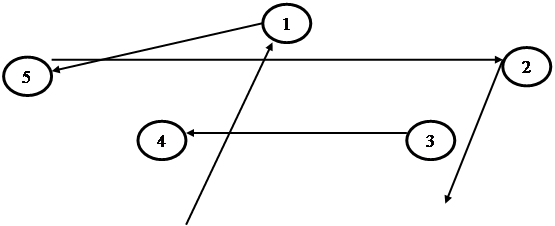
Рисунок 2.

Переходя от частной к общей постановке, задачу коммивояжера можно сформулировать как:

,

,

, (*)

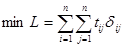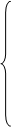
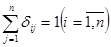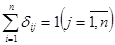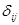= [0;1] .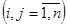