Электрический потенциал
Электростатическое поле, т.е. электрическое поле неподвижных зарядов, потенциально. Это означает, что работа электрического поля по перемещению пробного заряда по любому замкнутому контуру равна нулю: A = −q ∮ E→dr→ = 0. (7.1)
Потенциальность электростатического поля есть следствие закона сохранения энергии, ибо в противном случае можно было бы построить вечный двигатель 1-го рода.
Рис. 1.13:
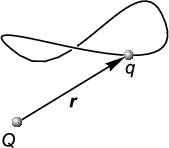
Доказательство равенства (7.1) очень просто. Вследствие принципа суперпозиции достаточно проверить, что равна нулю работа по замкнутому контуру в поле точечного заряда (рис. 1.13). Вычислим интеграл
A = −∫ r→ir→qQ r→dr→ r3 .
соответствующий работе по перемещению пробного заряда q в электрическом поле E→ = Qr→∕r3 заряда Q из начальной точки с радиус вектором r→i в наблюдения точку с радиус-вектором r→ по произвольному контуру. Дифференцируя тождество r→2 = r2, легко убедиться, что r→dr→ = rdr. Поэтому криволинейный интеграл сводится к определённому между радиусами ri и r начальной точки и точки наблюдения:
A = −∫ rirqQ dr r2 = qQ r −qQ ri .
Отсюда следует, что при любом выборе этих точек работа определяется только их положением и не зависит от формы пути. На замкнутом пути конечная точка совпадает с начальной, т.е. r = ri, поэтому A = 0.
Приведенное доказательство можно пояснить следующими рассуждениями. Любой контур можно представить в виде сегментов достаточно малого размера, поочередно идущих то по радиальному направлению от заряда Q, то по сферической поверхности, как показано на рис. 1.14.
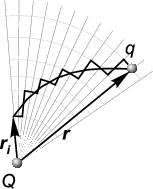
Рис. 1.14: Траектория перемещения пробного заряда и её приближение отрезками радиальных линий и дугами окружностей
Перемещение пробного заряда q по сфере перпендикулярно кулоновской силе, поэтому электрическое поле там не совершает работу. Все такие перемещения можно просто исключить. Тогда произвольный контур сжимается в отрезок прямой линии, идущей по радиусу от источника поля Q. Пробный заряд проходит этот отрезок дважды: сначала в одну сторону, потом обратно. На каждом участке обратного пути на него действует та же сила, что и при движении вперед, но так как заряд движется в противоположном направлении, работа имеет противоположный знак. Таким образом, при возвращении в точку старта работа электрического поля обращается в нуль.
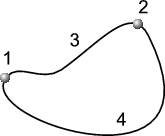
Рис. 1.15: Работа A132 по перемещению заряда в электростатическом поле из точки 1 в точку 2 по пути 132 равна работе A142 по перемещению того же заряда по пути 142. При перемещении заряда по замкнутому пути 13241 работа на участке 241 изменит знак: A241 = −A142. Поэтому A13241 = A132 + A241 = 0.
В потенциальном электрическом поле работа не зависит от формы пути. Это утверждение можно рассматривать в качестве альтернативного определения свойства потенциальности электрического поля. Два определения полностью эквиваленты, как должно быть ясно из приведенных выше рассуждений. Формальное же доказательство состоит в том, что если замкнутый контур разбить на две траектории, имеющие общие точки старта и финиша, то из равенства работы при перемещении пробного заряда по этим траекториям следует равенство нулю полной работы по замкнутому контуру (рис.1.15). И наоборот, из равенства нулю работы по замкнутому контуру следует равенство работы при перемещении пробного заряда по любым траекториям с общими точками старта и финиша.
Зафиксируем точку старта r→i, считая, что траектория перемещения заряда может финишировать в точке наблюдения с произвольными координатами r→ = (x,y,z) (рис. 1.14). Тогда интеграл ϕ(r→) = −∫ r→ir→E→⋅dr→ (7.2)
является однозначной функцией координат точки наблюдения, поскольку форма траектории не влияет на её значение. Функцию ϕ называют скалярным потенциалом электрического поля; используют также термины электростатический или электрический потенциал. Скалярный потенциал равен работе, совершаемой электрическим полем при перемещении единичного пробного заряда из точки наблюдения в ту точку, где потенциал условно принят равным нулю. Если нуль потенциала не задан, то говорят, что потенциал определен с точностью до аддитивной константы.
Пробный заряд q в электростатическом поле обладает потенциальной энергией U(r→) = q ϕ(r→). (7.3)
Потенциальная энергия также определена с точностью до константы. Имеет смысл только разность потенциальной энергии U(r→) − U(r→i) между двумя точками. Эта разность равна работе по перемещению заряда из точки r→i в точку r→: A = U(r→) − U(r→i). (7.4)
Потенциал точечного заряда Q нетрудно найти, повторив вычисления начала параграфа:
ϕ(r→) = −∫ rirQ dr r2 = Q r −Q ri .
Приняв за точку нуля бесконечно удаленную точку ri = ∞, получим ϕ = Q r. (7.5)
Если заряд qj находится в произвольной точке с радиус-вектором r→j, то
ϕ(r→) = qj ∣r→ −r→j∣.
Потенциал системы зарядов есть сумма потенциалов отдельных зарядов: ϕ(r→) = ∑ j q ∣r→ −r→j∣. (7.6)
Это следует из принципа суперпозиции.
В системе СИ потенциал измеряется в вольтах (В). В абсолютной гауссовой системе единицей измерения является статвольт (стВ): [ϕ] = 1стВ ≈ 300В. (7.7)
При перемещении заряда 1Кл между точками с разностью потенциала 1В совершается работа 1Дж, т.е. 1В = 1Дж∕Кл. Электрическое поле измеряется соответственно в вольтах на метр (В/м) и в статвольтах на сантиметр (стВ/см): [E] = 1стВ/см ≈ 3⋅104 В/м. (7.8)
Градиент потенциала.
Выразим теперь напряженность электрического поля через потенциал. Пусть 1 и 2 — две бесконечно близкие точки, расположенные на оси X, так что x2 − x1 = dx (рис. 1.16).

Работа при перемещении единичного заряда из точки 1 в точку 2 равна
Ex dx. Та же работа равна ϕ1 − ϕ2 = −dϕ. Приравнивая оба выражения, получим dϕ = −ex dx. Аналогичное рассуждение применимо для осей Y и Z. В результате находим все три компоненты вектора E→: E→ = −(∂ϕ ∂x, ∂ϕ ∂y, ∂ϕ ∂z). (8.1)
Так как E→ есть вектор, то и выражение, стоящее в правой части, есть вектор. Его называют градиентом скаляра ϕ и обозначают gradϕ, или ∇ϕ. Его можно рассматривать, как произведение дифференциального оператора
∇ = e→x ∂ ∂x + e→y ∂ ∂y + e→z ∂ ∂z
на скаляр ϕ. Теперь формулу (8.1) можно записать короче: E→ = −gradϕ = −∇ϕ. (8.2)
Она явно формула показывает несущественность аддитивной постоянной в определении потенциала: константа просто не влияет на результат дифференцирования.
Можно дать инвариантное определение градиента, которое будет верно в произвольной криволинейной системе координат. Градиент функции ϕ(r→) есть вектор, направленный в сторону максимального возрастания функции, а его длина равна производной функции в том же направлении. Чтобы пояснить смысл такого определения, проведем из произвольной точки r→ в каком-либо направлении единичный вектор s→. Проекция вектора A→ ≡ gradϕна это направление есть As = s→⋅A→ = s→⋅gradϕ. Но та же величина равна производной As = ∂ϕ∕∂s функции ϕ по направлению s→. В этом легко убедиться, проведя координатную ось в направлении вектора s→ и повторив рассуждения начала параграфа. Таким образом,
∂ϕ ∂s = s→⋅gradϕ.
Производная функции в каком-либо направлении равна проекции градиента этой функции на то же направление. Ясно, что эта производная максимальна, когда это направление совпадает с направлением градиента.
