Аналитические свойства оператора прямой задачи гравиметрии для распределения плотности

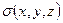Будем рассматривать в качестве модели среды – введенную в 2.1.1 модель распределения плотности в заданной области нижнего полупространства. В соответствии с (2.2) запишем связь между распределением плотности в области , целиком лежащей в нижнем полупространстве 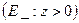, и вертикальной производной гравитационного потенциала в виде:

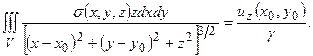(7.1)

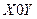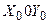Напомним, что координатные оси и совмещены, а ось 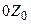направлена верх – противоположно оси 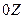. На первом этапе считаем, что вертикальная производная гравитационного потенциала задана на всей плоскости 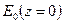: 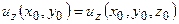. Тем самым, как хорошо известно, определены значения 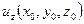в любой точке области 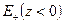- верхнего полупространства. В том числе и на поверхности произвольного рельефа, заданного функцией 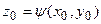. Значение это находится с помощью известного интеграла Пуассона (см. 2.1.4, формула (2.6)), дающего решение задачи Дирихле для полупространства:

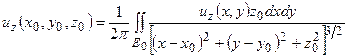. (7.2)

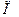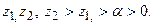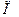Обозначим, кроме того – горизонтальную полосу в нижнем полупространстве (Е_), ограниченную по вертикали координатами В частности, область может совпадать с , либо быть ее собственным подмножеством. Соотношение (1), в соответствие с введенными ранее соглашениями об обозначениях операторов для прямой задачи, будем записывать в форме:

,

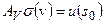где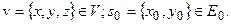

Следующий результат характеризует свойства непрерывности оператора .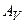

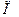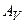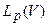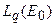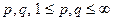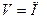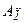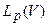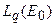Теорема 1. Пусть V – ограниченная область, целиком лежащая в . Тогда – линеен и ограничен из в для всех . Для случая оператор – линеен и ограничен из в при .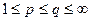

Обозначим 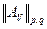- норму оператору 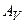, действующего из 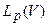в 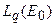. Тогда при ограниченной области :

,

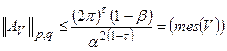где введены обозначения .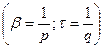

Для случая 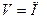и 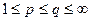величина 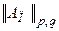ограничена и при :

.

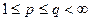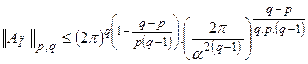В случае, когда q, либо одновременно q и p равны бесконечности:

, .

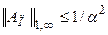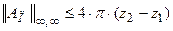Доказательство. Линейность – очевидное свойство введенного оператора. Доказать следует лишь его непрерывность в тех, либо иных, функциональных пространствах. Для краткости вместо:

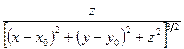
будем писать

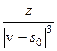, имея в виду, что 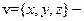пространственная координата точки в области .

Из (1) имеем:

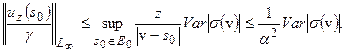
Далее:

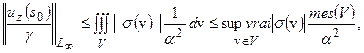
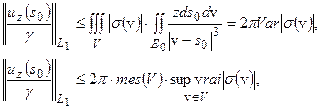
Следовательно:

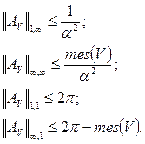
В силу теоремы Риса о выпуклости (прил.2), для 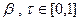имеем:

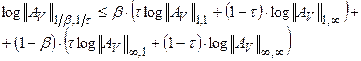
Следовательно:

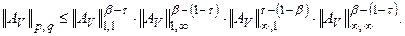
Тогда для 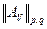легко получаем:

.

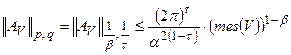Приведенная оценка является грубой. Она может быть улучшена для случая 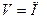. Заметим при этом, что если 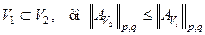. Таким образом, .

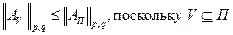Применим к соотношению (1) неравенство Юнга, рассматривая в качестве области V полосу П:

.

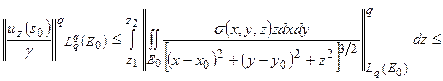
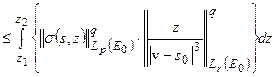Здесь 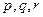связаны условием:

.

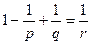Заметим, что, если 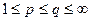, то это условие может быть выполнено при .

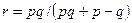Оценим величину:

.

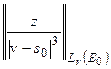Для этой цели вновь применим теорему Риса о выпуклости :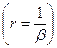

.

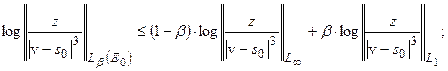
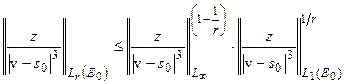Но:

.

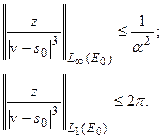Следовательно:

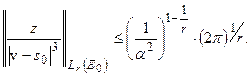
Тогда:

.

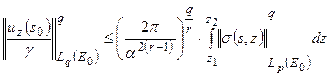(7.3)

Из (3) следует, что при 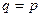и следующем отсюда :

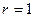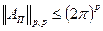. (7.4)

Теперь имеем следующую цепочку оценок:

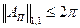; (7.5)

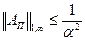; (7.6)

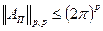. (7.7)

Из приведенных соотношений и неравенств Риса о выпуклости сразу следует вывод об ограниченности 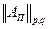для 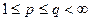. Рассмотрим теперь случай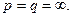

Обозначим 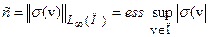. Понятно, что:

.

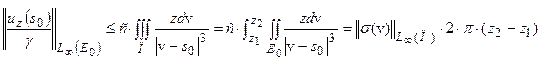Одно из утверждений теоремы доказано.

Оценим далее 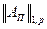, пользуясь для этого (4-7) и неравенством выпуклости:

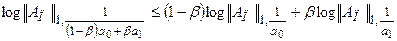
Полагая 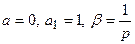, получим:

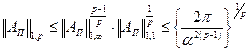. (7.8)

Теперь, используя (7) и неравенство выпуклости, найдем оценку для 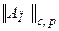, где :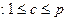

.

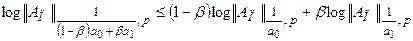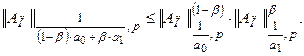
Примем 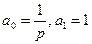, а β выберем так, чтобы .

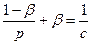Тогда 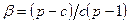, при этом 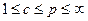. Тогда:

.

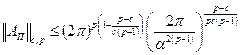Пользуясь обозначением 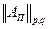, где p≤q , получим:

,

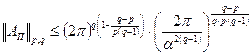или после упрощения:

,

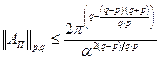что и требовалось доказать.

Итак, мы выяснили, что оператор 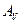является “хорошим” для решения прямых задач, поскольку линеен и ограничен во всех обозримых для приложения пространствах. Дифференцируя уравнение (1) по переменным 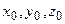, как по параметрам и, полагая z₀ = 0, получим новые операторы, соответствующие расчету высших производных гравитационного потенциала. Повторяя приведенные рассуждения, легко доказать, что вновь полученные операторы обладают теми же свойствами, что сформулированы в теореме 1. 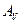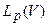По тем же причинам непрерывен оператор из в 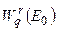и т.д. Однако нас, в большей мере, интересует обратная задача, и главным свойством является ее разрешимость. Следует выявить, при каких правых частях уравнение (1) разрешимо, является ли решение единственным и будит ли оно устойчивым. Для простоты дальнейших рассмотрений ограничимся случаем, когда 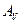действует из 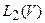в .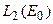

Теорема 2. Пусть – область в 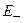, целиком лежащая в П и содержащая некоторый шар в 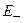. Тогда 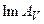образует в 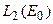плотное множество[29].

Доказательство. Воспользуемся тем фактом, что плотность 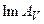в 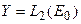эквивалентна однозначной разрешимости сопряженного уравнения. Действительно, поскольку 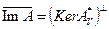, то из условия 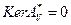следует 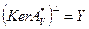и 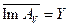. Вид сопряженного к 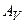оператора 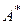, отображающего пространство 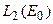в подпространство в 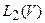, определен соотношением:

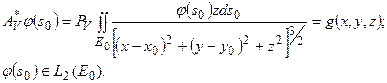(7.9)

Где 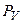– проектор из 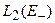на 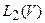. Это следует из следующей цепочки равенств:

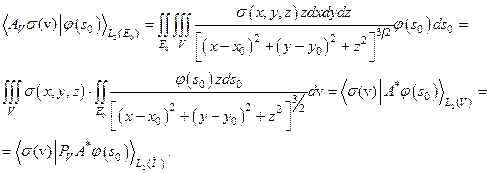(7.10)

Легко заметить, что 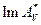- множество гармонических в V и непрерывных на границе V функций, имеющих единственное аналитическое продолжение на все E_ (так как V содержит некоторый шар). Но равенство нулю гармонической функции внутри некоторого шара влечет ее равенство нулю всюду в области гармоничности. В частности, из:

,

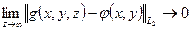следует, что уравнение 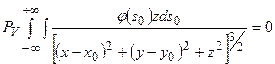имеет единственное решение 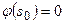. Таким образом, 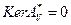, теорема доказана.

Из приведенного результата следует вывод о том, что уравнение (1) может быть решено как угодно точно для любой правой части из 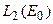. Но разрешимость с любой наперед заданной точностью не означает строгой разрешимости. В каком-то смысле, элементов из 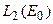, для которых уравнение (1) не имеет строгого решения, даже больше, чем тех, для которых имеет, т.е. чем 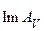. Более строгий смысл придает сказанному .

Теорема 3. Пусть 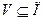, тогда 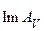образует 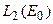множество первой категории.

Доказательство. Напомним, что М есть множество первой категории, если оно представимо, как не более, чем счетное объединение нигде не плотных множеств. Множество называется нигде не плотным, если его замыкание не содержит внутренних точек.

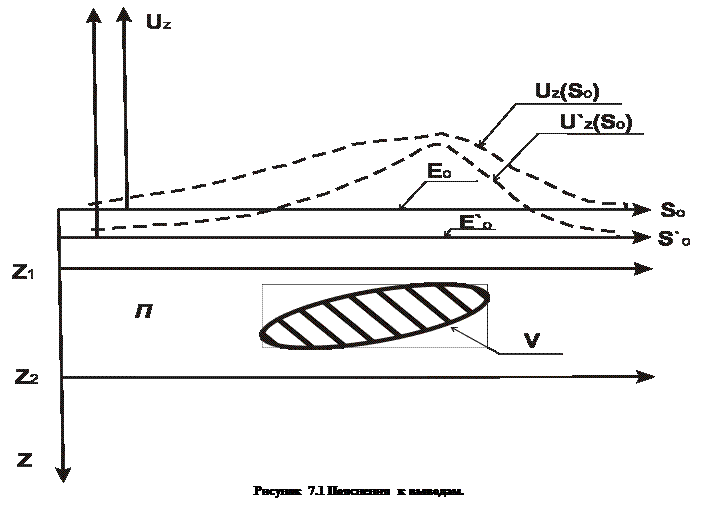
Выберем плоскость 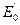, определенную значением вертикальной координаты 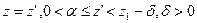, что возможно в силу определения П. (см. рис. 1).

Значение поля 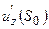на 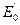от распределения масс в V равно:

.

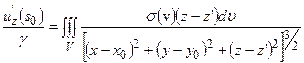В силу доказанной выше теоремы 1 о непрерывности оператора (1) 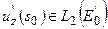и, следовательно, 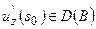, где 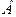оператор, определенный как интеграл Пуассона:

.

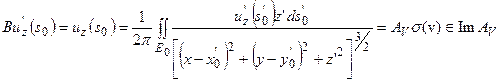Следовательно, 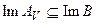. Осталось показать, что 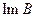множество первой категории.

Пусть S – замкнутый единичный шар в 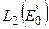. Поскольку для любого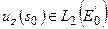

,

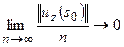то 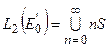. Тогда 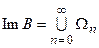, где 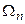– образ 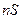при отображении 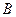. В силу ограниченности 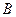и рефлексивности 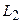, каждое из 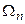замкнуто как образ замкнутого выпуклого множества. Если 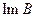– множество второй категории, то хотя бы для одного n Ω_n, в силу замкнутости, имеет внутреннюю точку. Но если оператор (линейный и ограниченный) отображает замкнутый шар во множество, имеющее внутреннюю точку, то обратный к этому оператору ограничен. Покажем теперь, что оператор 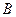не имеет ограниченного обратного, как оператор из 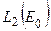в себя (в ).

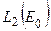Рассмотрим уравнение :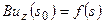

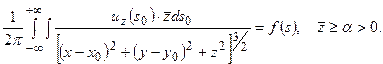(7.11)

Выберем последовательность монотонно убывающих чисел 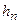, предел которых равен 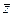, и соответствующую им, параметризированных числами 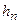последовательность функций:

.

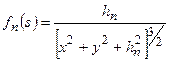Ясно, что 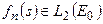, так как 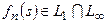и по теореме Рисса о выпуклости:

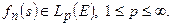
Последовательности 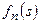соответствует последовательности

,

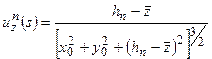Поскольку, как это следует из (11):

.

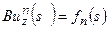Однако последовательность 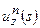не имеет предела в 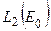, в то время как последовательность 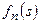такой предел имеет:

.

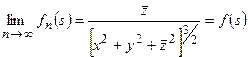Итак, имеем: 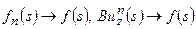, однако 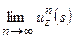не существует в 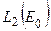. Но это не совместимо с предположением ограниченности оператора 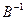как действующего из 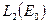в 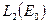. Таким образом, приходим к выводу, что 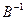не ограничен и, следовательно, 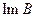не имеет внутренней точки. Тогда 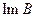есть множество первой категории, что и требовалось доказать.

Замечание: Все рассмотренные последовательности принадлежат и 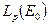. Следовательно, приведенный пример “работает” во всех этих пространствах. Более того, основным моментом в доказательстве теоремы является вывод о замкнутости образа S при отображении В. Это имеет место для всех рефлексивных пространств, и теорема 3 верна для всех .

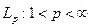Рассмотрим теперь вопрос о единственности решения уравнения (1), предполагая, что хотя бы одно решение существует. В силу линейности оператора 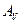, утверждению о существовании более чем одного решения уравнения (1) эквивалентно утверждение о существовании ненулевых решений уравнения 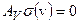. Последнее означает, что ядро 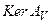оператора 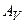содержит и ненулевые элементы. Действительно, если два распределения плотност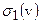и и 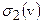удовлетворяют одному и тому же уравнению 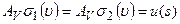, то 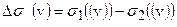удовлетворяет уравнению .

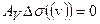Простейший и известный еще Ньютону пример гравитационной эквивалентности двух различных тел – это совпадение внешних гравитационных полей от двух однородных по плотности шаров с общим центром и массой, но различной плотности и, как следствие, различного радиуса. Уже из этого примера можно заключить, что ядро оператора 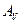содержит более одного элемента.

Полное описание ядра оператора 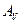дает следующая теорема.

Теорема 4 (П.С.Новиков). Пусть V – замкнутая регулярная область. Для того, чтобы распределение плотности 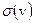создало нулевой внешний потенциал, необходимо и достаточно, чтобы для любой гармонической в V и непрерывной на границе 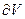области V функции 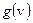выполнялось равенство

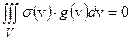. (7.12.)

По сути это означает, что ядро 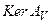оператора 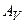ортогонально множеству гармонических в V и непрерывных на 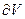функций.

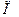Замечание 1. Теорема не распространяется на случай, когда в качестве области выступает полоса , поскольку последняя не замкнута. Более того, далее будет показано, что для случая 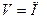существуют гармонические в 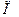функции, с нулевой правой частью для (1).

Замечание 2. Существенным является и требование, чтобы нулю равнялась правая часть в (1) только всюду на 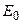. Далее будет показано, что для любого конечного множества точек 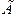из 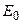, или более обще 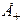, существует гармоническая в V функция, для которой правая часть в (1) отображается в ноль во всех точках .

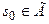Теорему 3 можно легко вывести из теоремы о ядре (см. приложение 2.4). Действительно, согласно теореме о ядре 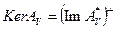. Поскольку 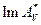- множество гармонических в V функций, представимых в виде интеграла Пуассона, замыкание которых для регулярной области V есть также гармонические в V функции, непрерывные на границе 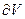, то и получаем требуемый результат.

Теорема о ядре позволяет сформулировать результат о единственности решения уравнения (1) и для поточечно заданного поля.

Теорема 5. Пусть область V ограничена и замкнута. Для того чтобы распределение плотности создавало нулевую вертикальную производную гравитационного потенциала в N точках 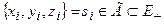, необходимо и достаточно, чтобы для любой из N функций

,

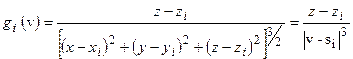выполнялось условие:

.

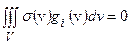Для доказательства достаточно применить теорему о ядре, в соответствии с которой 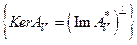к оператору:

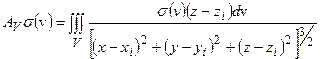, отображающему 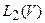в систему из 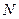значений поля 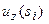, образующих конечномерное пространство 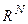с Евклидовой нормой.

Для того чтобы найти сопряженный этому оператору, выберем произвольный вектор 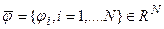из сопряженного к 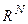пространства, совпадающего с самим 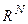, и запишем цепочку равенств:

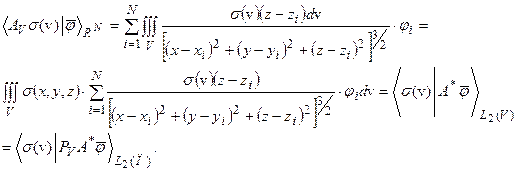
Следовательно, искомый сопряженныйимеет вид:

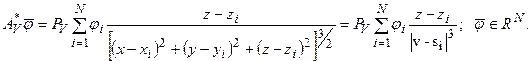
Ясно, что из условия 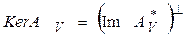следует, что для любого элемента 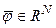и 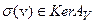выполнено 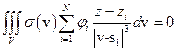. Но тогда выполнено и (12) .

Из теоремы П.С.Новикова следует, что множество гармонических и непрерывных на границе ограниченной, регулярной, замкнутой области V есть класс единственности. Условие ограниченности области, как это было отмечено в замечании 1 весьма существенно. Без этого условия теорема не работает.

Покажем, что если область V не ограничена, то существует гармонические распределения плотности в V с нулевым значением вертикальной производной гравитационного потенциала на .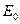

К уравнению 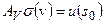применим преобразование Фурье (по 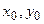). Получим:

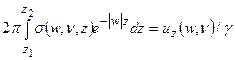(7.13)

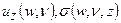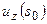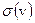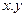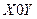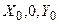Где - есть преобразование Фурье функций и по переменным соответственно (напомним, что оси и совмещены), а .

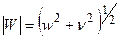Будем искать теперь решение уравнения (13) в виде

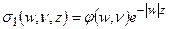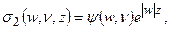и соответственно. Здесь: 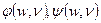- искомые функции. После тривиальныхподстановок выражений для 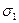и 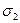в (13) получаем:

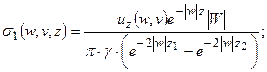(7.14)

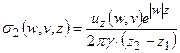. (7.15)

Если функцию 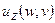выбрать так, чтобы функция 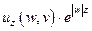была квадратично интегрируемой при 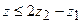и, следовательно, квадратично интегрируемо и ее обратное преобразование Фурье для этих значений 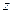, то, в силу неравенств 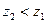и

,

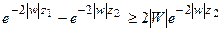формулой (14) определен некоторый элемент из 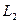, преобразование Фурье (обратное) которого есть гармоническая функция. Точно также обратное преобразование Фурье функции (15) по переменным 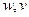есть гармоническая функция, и наложенных ранее условий на 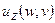достаточно, чтобы соотношением (15) была определена функция из 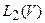. Каждая из них соответствует одному и тому же полю, спектр которого есть 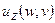. Беря их разность, получаем, что соотношением

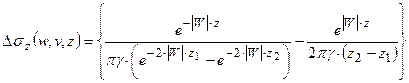(7.16)

определена функция, обратное преобразование Фурье которой по переменным 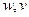есть гармоническая функция (в силу гармоничност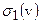и и 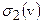), и этой функции соответствует нулевое значение вертикальной производной гравитационного потенциала на 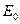. Таким образом, для неограниченной области существуют гармонические функции, принадлежащие ядру оператора прямой задачи с полем на .

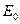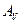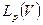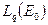Поскольку - линейный ограниченный оператор из в , то 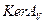- замкнутое пространство в 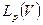. Следовательно, можно определить фактор-пространство 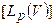пространства 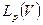по ядру оператора 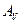. Это пространство состоит из классов смежности, вместе с заданным элементом, содержащим и все элементы, эквивалентные ему по гравитационному полю. Иными словами, классами смежности являются всевозможные элементы вида 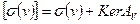. Легко проверить, что два класса смежности либо совпадают, либо не пересекаются. 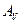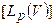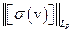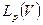Оператор , рассматриваемый на фактор - пространстве , уже является взаимнооднозначным и непрерывным, если норму в определить условием:

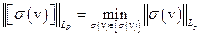. (7.17)

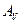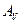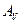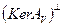Область значений этого оператора совпадает с областью значений оператора , а область определения есть банахово пространство, состоящее из описанных классов смежности. Тогда, в силу доказанной теоремы 3, не может иметь ограниченного обратного. Эквивалентное этому утверждению – сужение на не имеет ограниченного обратного.

Проведенный анализприводит к следующим выводам:

1. Обратная задача в классе распределений плотности может быть решена для любой правой части из 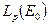с любой наперед заданной точностью.

2. Решение неединственное и определено с точностью до произвольного элемента из 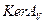, являющегося замкнутым подпространством в .

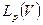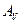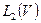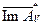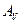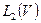3. Оператор , определенный на подпространстве в , состоящем из распределений, принадлежащих , не имеет ограниченного обратного. Иными словами, сужение с на 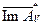не имеет ограниченного обратного.

Таким образом, обратная задача гравиметрии является некорректной. Для нее не выполнено ни одного из условий корректности по Адамару.

В процессе доказательства того, что множество значений оператора (1) есть множество первой категории в 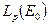при 1<p<∞, было показано, что таковой является и область значений оператора (11), доставляющего решение задачи Дирихле для полупространства. Это означает, что обратная задача для (11) является неустойчивой из 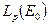в 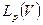и, кроме того, не для всех 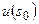из 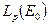она разрешима. Итак, для задачи аналитического продолжения потенциального поля в нижнее полупространство (обратная задача к аналитическому продолжению поля в верхнее полупространство, доставляемому интегралом Пуассона): решение не всегда существует, решение не устойчиво из 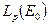в .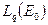

Нетрудно доказать и то, что оператор В имеет в качестве области значений множество первой категории и в пространстве непрерывных на 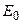функций 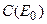. Для этого следует продемонстрировать неограниченность обратного оператора на пространстве функций 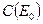. Рассмотрим множество из 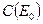функций, производная которых в направлении оси 0Y равна нулю (выполнены условия двухмерности). Тогда аналог соотношение (11) запишется так:

,

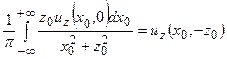где 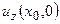и 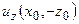- след на оси 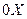функци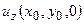й и 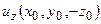, соответственно. Выберем в качестве 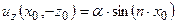. Тогда под интегралом, для того чтобы он превратился в тождество, необходимо поставить вместо 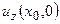функцию 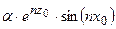. При 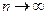последовательность 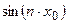слабо сходится к нулю, в тоже время 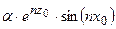, при 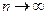не является слабо сходящей последовательностью. Это противоречит требованию непрерывности. Таким образом, оператор, обратный к В, не является слабо непрерывным, тем более он не является и сильно непрерывным.