Сведение задачи открытого типа к задаче закрытого типа

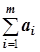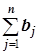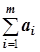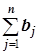Выше мы уже отметили, что задача открытого типа решается сведением её к задаче закрытого типа введением фиктивных либо потребителя П_n+1 с потребностью b_n+1= - (при > ), либо поставщика P_m+1 с запасом a_m+1= 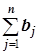- 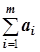(при 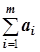< 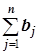). При этом стоимости c перевозок с фиктивными участниками делается произвольным постоянным числом, например, c=0. Далее задача решается обычным образом. Только ответ формулируется с реальными перевозками (без учёта фиктивных перевозок).

Пример 7. Решить транспортную задачу, предварительно сведя её к задаче закрытого типа:

bj ai

Решение. Имеем 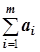=50+60+90+30=230 и 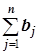=40+60+50+50=200, то есть 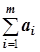¹ 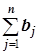. При этом 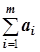> 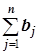, то есть у поставщиков имеется излишки груза. Вводим фиктивного потребителя с b₅= 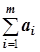- 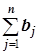=30 единицами груза и нулевыми стоимостями перевозок:

bj ai

Находим оптимальное решение закрытой задачи:

bj ai

Вычисляем стоимость перевозок:

30×3+20×4+10×3+50×3+30×4+30×4+30×3=680.

В ответе не учитываются перевозки к фиктивному потребителю. Таким образом, 30 единиц груза третьего поставщика остаются невостребованными.

Ответ: Матрица перевозок: 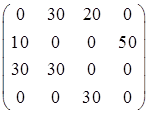. Стоимость перевозок F_min=680 у.е.

Упражнения.

1) Составить первоначальный опорный план следующих задач:

а) методом северо-западного угла;

б) методом наименьших затрат:

bj ai						bj ai

Найти решение задачи.

2) Решить транспортные задачи. Первоначальный опорный план составить двумя методами

bj ai						bj ai

Приложения

Приложение 1. Задания для индивидуальных работ

Задание 1

Решить задачу графическим методом (найти оба экстремума целевой функции)

Вариант	Задача	Вариант	Задача
	F=2x1+3x2®max (min)	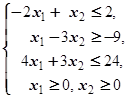	F=5x1+5x2® max (min)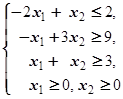
	F=5x1-3x2® max (min)	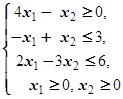	F=-x1-x2® max (min)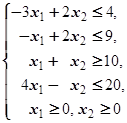
	F=2x1+3x2® max (min)	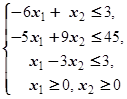	F=5x1-x2® max (min)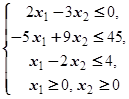
	F=2x1+2x2® max (min)	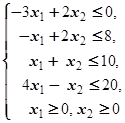	F=4x1+2x2® max (min)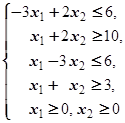
	F=2x1+4x2® max (min)	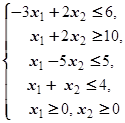	F=-3x1-x2® max (min)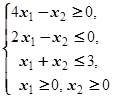

	F=15x1+10x2® max (min)	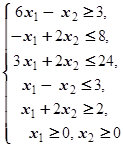	F=2x1+3x2® max (min)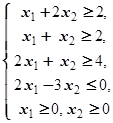
	F=3x1+2x2® max (min)	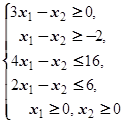	F=4x1+6x2® max (min)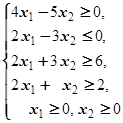
	F=2x1+5x2® max (min)	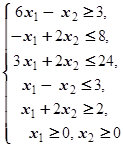	F=-x1+4x2® max (min)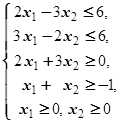
	F=2x1-x2® max (min)	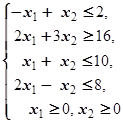	F=x1+4x2® max (min)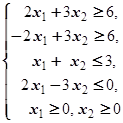
	F=3x1+2x2® max (min)	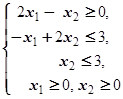	F=x1-4x2® max (min)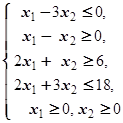

	F=2x1+4x2® max (min)	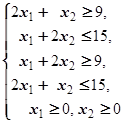	F=-5x1+x2® max (min)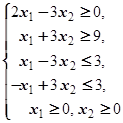
	F=x1-3x2® max (min)	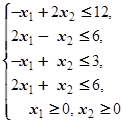	F=4x1+3x2® max (min)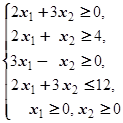
	F=3x1-x2® max (min)	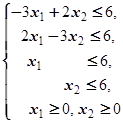	F=2x1+3x2® max (min)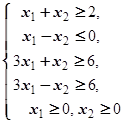
	F=x1-2x2® max (min)	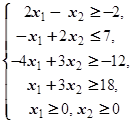	F=3x1-x2® max (min)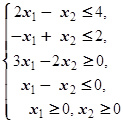
	F=3x1+6x2® max (min)	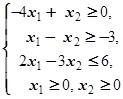	F=3x1+4x2® max (min)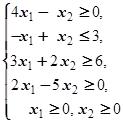

Задание 2

1) Решить задачу линейного программирования (найти оба экстремума):

а) симплекс-методом;

б) методом искусственного базиса.

2) Составить для обеих экстремумов двойственную и найти её решение по решению исходной:

Вариант	Задача	Вариант	Задача
	F=x1+4x2+x3®max (min)	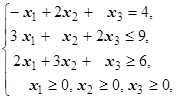	F=-2x1-2x2-2x3® max (min)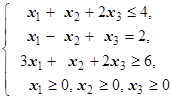
	F=2x1+3x2-x3® max (min)	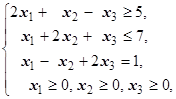	F=-3x1-2x2-2x3® max (min)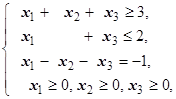
	F=x1-x2+x3® max (min)	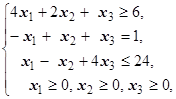	F=-2x1+8x2+3x3® max (min)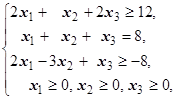
	F=5x1+2x2+x3® max (min)	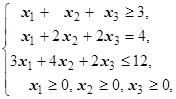	F=6x1+7x2+9x3® max (min)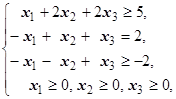
	F=x1-8x2-3x3® max (min)	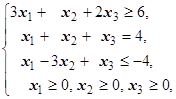	F=5x1+2x2+x3® max (min)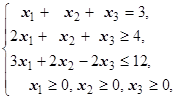
	F=-x1-3x2-x3® max (min)	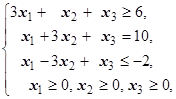	F=6x1-x2+3x3® max (min)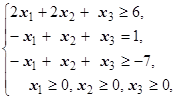
	F=x1+4x2+3x3® max (min)	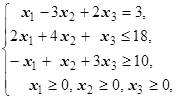	F=2x1+2x2-x3® max (min)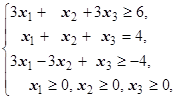
	F=-4x1-3x2-2x3® max (min)	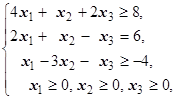	F=x1+3x2+x3® max (min)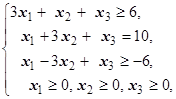
	F=4x1+x2+3x3® max (min)	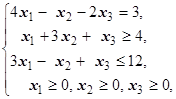	F=2x1+3x2+2x3® max (min)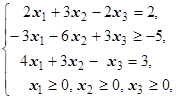
	F=x1-3x2-2x3® max (min)	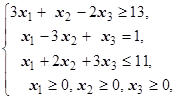	F=2x1+2x2-5x3® max (min)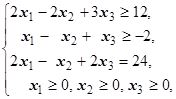
	F=3x1+2x2+2x3® max (min)	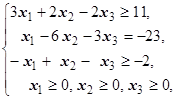	F=x1+2x2+2x3® max (min)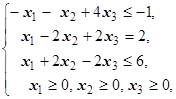
	F=3x1+2x2+3x3® max (min)	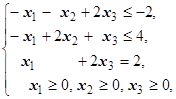	F=5x1+7x2+9x3® max (min)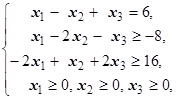
	F=x1+2x2+x3® max (min)	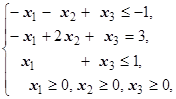	F=x1+x2-4x3® max (min)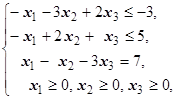

	F=2x1+x2+2x3® max (min)	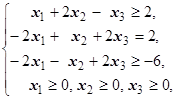	F=3x1+2x2-3x3® max (min)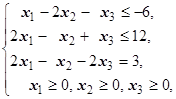
	F=6x1+7x2+9x3® max (min)	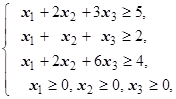	F=-3x1+x2+2x3® max (min)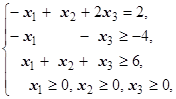

Задание 3

1) Решить задачу об использовании сырья симплекс-методом. Дать экономическую интерпретацию задачи.

2) Решить задачу о диете (рационе).

Условия задач приведены в таблице. Во всех случаях составить математическую модель задачи.

Значения коэффициентов условия задачи
	Вариант 1			Вариант 2
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 3			Вариант 4
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 5			Вариант 6
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 7			Вариант 8
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj

	Вариант 9			Вариант 10
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 11			Вариант 12
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 13			Вариант 14
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 15			Вариант 16
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 17			Вариант 18
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 19			Вариант 20
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 21			Вариант 22
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 23			Вариант 24
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 25			Вариант 26
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 27			Вариант 28
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj
	Вариант 29			Вариант 30
Si	bi	P1	P2		Si	bi	P1	P2
S1					S1
S2					S2
S3					S3
	cj					cj

Задание 4

Решить задачи Задания 1 как задачу целочисленного программирования.

Задание 5

Решить задачи Задания 2 как задачу целочисленного программирования.

Задание 6

Решить транспортную задачу методом потенциалов. Первоначальный план составить методами северо-западного угла и наименьших затрат.

Значения коэффициентов условия задачи

Вар-т 1

Потребители и их потребности

Вар-т 2

Потребители и их потребности

Пос-тав-щики и их запа- сы

Пос-тав-щики и их запа- сы

Вар-т 3

Потребители и их потребности

Вар-т 4

Потребители и их потребности

Пос-тав-щики и их запа- сы

Пос-тав-щики и их запа- сы

Вар-т 5

Потребители и их потребности

Вар-т 6

Потребители и их потребности

Пос-тав-щики и их запа- сы

Пос-тав-щики и их запа- сы

Вар-т 7

Потребители и их потребности

Вар-т 8

Потребители и их потребности

Пос-тав-щики и их запа- сы

Пос-тав-щики и их запа- сы

Вар-т 9

Потребители и их потребности

Вар. 10

Потребители и их потребности

Пос-тав-щики и их запа- сы

Пос-тав-щики и их запа- сы

Вар. 11

Потребители и их потребности

Вар. 12

Потребители и их потребности

Пос-тав-щики и их запа- сы

Пос-тав-щики и их запа- сы