Вопрос 3. Физический и геометрический смысл производной

Физический (механический) смысл

Вытекает из задачи о скорости прямолинейного движения.

Скорость ʋ прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t:

ʋ = S′(t).

По аналогии с этим производную любой функции часто называют скоростью изменения этой функции.

Геометрический смысл

Пусть на плоскости Оху кривая задана уравнением у = f(х). Требуется провести касательную к кривой в данной точке М(х,у), где у = f(х).

Так как точка касания дана, то для решения задачи необходимо найти угловой коэффициент искомой касательной, т.е. k = tgα, где α - угол наклона касательной к оси Ох.

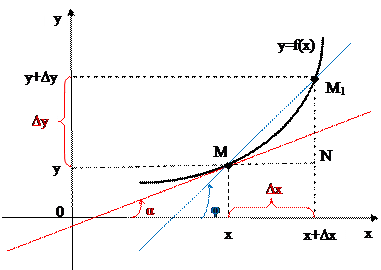Выберем на той же кривой точку М₁(х+∆х,у+∆у), где у+∆у = f(х+∆х). Отсюда

∆у = f(х+∆х) ‒ у или ∆у = f(х+∆х) ‒ f(х).

Проведем через точки М и М₁ секущую ММ₁ и обозначим угол ее наклона через φ.

0.3.1. Касательной к данной кривой у = f(х) в точке М называется предельное положение секущей ММ₁ при стремлении точки М₁ к точке М по кривой (т.е. при ∆х→0).

Если М₁→М при ∆х→0, то 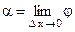и

И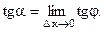з рисунка видно, что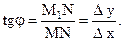

Следовательно,

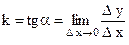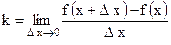или . (2)

Равенство (2) можно переписать в виде

.

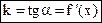Таким образом, угловой коэффициент k касательной к кривой у = f(х) в точке с абсциссой х есть производная f′(х).

Если точка касания М имеет координаты (х₀,у₀), то угловой коэффициент касательной k = f′(х₀). Пользуясь уравнением прямой, проходящей через данную точку в заданном направлении, которое имеет вид:

у ‒ у₀ = k(х ‒ х₀),

можно записать уравнение касательной к кривой у = f(х) в точке М(х₀,у₀):

.

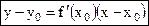0.3.2. Прямая, проходящая через точку касания, перпендикулярно касательной называется нормалью к кривой.

Используя условие перпендикулярности прямых на плоскости, получим уравнение нормали:

,

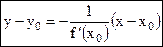при условии, что .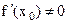

Вопрос 4. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности

О.4.1.Функция у = f(х) называется дифференцируемой в точке х, если ее приращение ∆у в этой точке можно представить в виде

∆у = А∆х + α(∆х) ∆х, (3)

где А – некоторое число, не зависящее от ∆х; α(∆х) - функция аргумента ∆х, являющаяся бесконечно малой при ∆х→0, т.е. .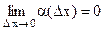

Установим связь между дифференцируемостью функции в точке и существованием производной в той же точке.

Т.4.1.(связь между дифференцируемостью и существованием производной в точке)

Для того чтобы функция у = f(х) была дифференцируема в точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

В этом случае в равенстве (3): А = f′(х).

Следующая теорема устанавливает связь между понятиями дифференцируемости и непрерывности функции.

Т.4.2. (связь между дифференцируемостью и непрерывностью функции)

Если функция у = f(х) дифференцируема в точке х, то в этой точке она непрерывна.

Замечание

Обратная теорема не верна: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми.

Пример 2. Функция 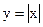непрерывна в точке х =0, но не имеет производной в этой точке (т.к. в точке х = 0 графика функции не существует касательной).

Следовательно, непрерывность функции является необходимым, но не достаточным условием дифференцируемости функции.

О.4.2.Функция у = f(х), дифференцируемая в каждой точке множества Х, называется дифференцируемой на множествеХ.