Штейнберг А. Правило фаз Гиббса //Квант. €

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Содержание [убрать] · 1 Что такое фаза? · 2 Знакомство с фазовыми диаграммами · 3 Правило фаз в однокомпонентных системах · 4 Правило фаз для многокомпонентных систем · 5 Примечания

Просто удивительно, сколько интересных вопросов может возникнуть при наблюдении самых обычных явлений. Ну, например... Почему лед и вода, не превращаясь друг в друга, существуют только при 0 °С? Чуть изменится температура — и либо лед начнет таять, либо вода начнет замерзать. Для нас это, конечно, счастливое обстоятельство, ведь иначе слякоть и гололед случались бы значительно чаще. И все же: почему это так? Сразу, разумеется, не ответишь, зато первый вопрос вызывает цепочку других. Услужливая память подсказывает, что у воды существует и третье «обличье» — водяной пар. Так вот, могут ли вода, пар и лед существовать в одном сосуде одновременно, не превращаясь друг в друга? Скорее всего, ответ на этот вопрос вы знаете. Но возьмите любой элемент из таблицы Менделеева. Почти каждый может существовать и в жидком, и в твердом, и в газообразном состоянии. А одновременно, в одном сосуде?

Как вы уже догадались, в этой статье мы попытаемся ответить на эти и многие другие вопросы. Для этого давайте попробуем пройти узкой тропинкой удивительных выводов, которую более 100 лет назад открыл великий американский физик Джозайя Виллард Гиббс.

Что такое фаза?

Слово «фаза» имеет множество значений. Интересующее нас введено в практику Гиббсом. Чтобы понять, что же такое фаза по Гиббсу, начнем с примеров.

При 0 °С в уличных лужах появляются кусочки льда. Первоначально однородная система — жидкая вода — распадается на две части. Их называют двумя разными фазами химического соединения Н₂О. То же самое соединение может существовать и в виде третьей фазы — водяного пара.

Жидкость, кристалл и пар — самые привычные примеры разных фаз одного вещества. Однако фазы не обязательно различаются между собой именно агрегатным состоянием. Хорошо известны две твердые фазы углерода — графит и алмаз. Они имеют разные кристаллические решетки, и это приводит к колоссальному различию их свойств. Фазы могут отличаться друг от друга и по своему химическому составу, и по магнитным характеристикам (магнитная и немагнитная), и по электрической проводимости (нормальная и сверхпроводящая), и по другим свойствам.

Теперь попытаемся ввести понятие фазы более строго. За основу возьмем лаконичное определение академика М. А. Леонтовича: «В термодинамике фазой называется всякая однородная система, т. е. тело, физические свойства которого во всех точках одинаковы». Здесь надо отметить несколько тонкостей.

Во-первых, говоря о «теле», мы всегда подразумеваем, что оно состоит из большого количества микрочастиц — атомов или молекул. Как правило, мерой «большого количества» служит число Авогадро — 6·10²³.

Фигурирующую в определении «однородность» тоже надо понимать на уровне «большого числа» частиц, а не отдельных атомов или молекул. Воздух — однороден и является однофазной системой, хотя и состоит из разных молекул.

В многофазной системе однородность теряется, как это было в случае льда и воды. Между разными фазами одной системы обычно существует четко выраженная поверхность раздела. Приведем здесь еще один пример. Возьмите емкость с подсолнечным маслом и накапайте туда воду. Жидкости не смешаются. Вода в масле образует свою отдельную фазу. Поверхность раздела между двумя фазами будет отчетливо видна.

Не всегда неоднородность системы и поверхность раздела видны невооруженным глазом. Сталь, например, выглядит вполне однородно, и лишь с помощью микроскопа убеждаешься в ее многофазности.

Фотографии фазовых структур стали и бронзы, сделанные с помощью микроскопа

При изменении внешних условий (температуры, давления, электрического или магнитного полей) фазы могут превращаться друг в друга (это вполне понятно уже на примере воды, пара и льда). Эти процессы так и называются — фазовые превращения.

Знакомство с фазовыми диаграммами

Начнем изучение фазовых превращений все с той же чистой воды. Для этого заключим ее в герметичный сосуд с поршнем, где ее состоянием легко управлять, меняя внешнее давление на поршень и нагревая или охлаждая сосуд. Важно понять, что никаких других способов воздействовать на фазовое состояние воды в сосуде, его при этом не открывая, у нас нет^[1]. Поэтому все «события», связанные с фазовыми превращениями в замкнутом сосуде, должны быть функцией только р и Т.

Обратим внимание на одно обстоятельство: если во внешней среде поддерживается постоянная температура Т, то через некоторое время такая же температура установится во всех фазах системы. Это положение подтверждается нашим каждодневным опытом — при наличии контакта температуры разных тел выравниваются.

То же самое справедливо и в отношении давления, но с одной оговоркой: давление в разных фазах одинаково и равно внешнему, если все поверхности раздела между фазами плоские^[2]. Тогда равенство давлений сразу следует из механического равновесия поверхности раздела. Если же поверхности раздела имеют конечный радиус закругления, то приходится принимать во внимание и силы поверхностного натяжения. Однако в дальнейшем мы будем предполагать, что границы фаз всегда плоские. С учетом этих замечаний состояние системы характеризуется общими для всех фаз значениями давления и температуры.

Прежде всего желательно выяснить, при каких внешних условиях происходит фазовое превращение. Для определенности остановимся на испарении воды. Если зафиксировать нормальное атмосферное давление, то вода в нашем сосуде начнет испаряться при 100 °С. При более низких температурах поршень в сосуде будет «лежать» на воде, и пара в системе не будет.

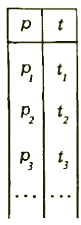
Рис. 1

Изменив давление, мы изменим и температуру начала испарения. Можно свести все данные о фазовом превращении в таблицу из двух колонок: в одной указывать давление, а в другой — температуру начала испарения. Но еще удобнее изобразить данные таблицы графически в виде зависимости температуры от давления (рис. 1). Точно так же можно в виде графиков представить данные и о двух других фазовых превращениях, которые могут происходить в системе,— превращениях вода ⇔ лед и лед ⇔ пар. В результате получим такую диаграмму, как на рисунке 2.

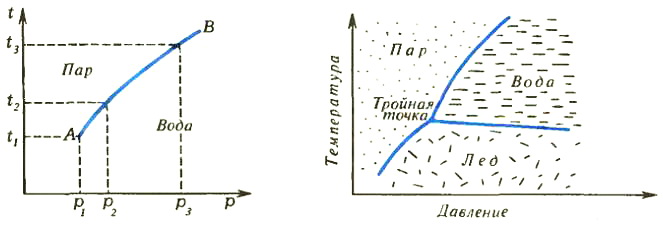
Рис. 2

Подчеркнем одно важное обстоятельство. Линии на диаграмме отделяют друг от друга области устойчивого существования соответствующих фаз. Это отнюдь не означает, будто каждая фаза «живет» только в своей области и не может «залезать» в чужую. Разумеется, может. Мы регулярно наблюдаем это, скажем, весной, когда уже при положительной температуре реки еще полны льдин. Но такое состояние не является устойчивым — лед в реке тает. Этот процесс происходит не мгновенно, а с какой-то конечной скоростью. Через несколько дней (если вновь не ударят морозы) лед обязательно растает весь, до конца. А вот вода при тех же условиях уже никогда снова не станет льдом.

Если состояние системы перестает меняться во времени, говорят, что в ней установилось равновесие. Диаграмма на рисунке 2 предсказывает только равновесное состояние системы.

Подобные диаграммы называют фазовыми. Ими очень удобно пользоваться: зная температуру и давление, сразу определяем, из каких фаз система будет состоять в равновесии. Определенным значениям давления и температуры на диаграмме соответствует точка. Если она попадает в области устойчивого существования пара, льда или жидкости, то в равновесии система будет состоять из одной соответствующей фазы. Если точка оказывается на линии диаграммы, система в равновесии будет состоять из двух фаз. Из каких именно? Совершенно очевидно: если, например, это — линия раздела «водной» и «ледяной» областей, то из льда и воды. И наконец, при единственном сочетании давления и температуры в равновесии будут находиться все три фазы.

Правило фаз в однокомпонентных системах

Не почувствовали вы по диаграмме воды, что имеются какие-то законы, регламентирующие «условия жизни» фаз? Посудите сами: в однофазном состоянии система может существовать в широком диапазоне давлений и температур, в двухфазном — только при их определенных комбинациях, а трехфазная область на диаграмме вообще стягивается в точку. Так и хочется представить фазы в роли жильцов коммунальной квартиры: чем больше жильцов, тем меньше свободы у каждого из них. Впрочем, нельзя делать выводы на основании диаграммы одного-единственного вещества. А вдруг в другом все по-другому?

И все-таки закон совместного существования фаз действительно есть. По имени своего первооткрывателя он называется правилом фаз Гиббса.

Во всех биографиях американского физика-теоретика Дж. Гиббса (1839 - 1903) подчеркивается, что жизнь этого человека была внешне бедна событиями. Все его силы были сконцентрированы на получении научных результатов, блеск которых не потускнел и сегодня. Со времени опубликования последней работы Гиббса прошло более 80 лет, а результаты его исследований продолжают использоваться в практически неизменном виде.

Правило фаз всегда считалось одним из самых значительных достижений Гиббса. Строгий вывод правила достаточно сложен. Мы приведем его в существенно упрощенном виде.

Начнем рассмотрение все с той же воды, находящейся в замкнутом сосуде^[3]. Предположим, что при данных значениях р и Т в равновесии находятся жидкая фаза и пар. Молекулы Н₂О в паре и в жидкости находятся в непрестанном тепловом движении. В результате некоторые из них покидают свою «родную» фазу и попадают в соседнюю. Среднее количество молекул, которые улетают за единицу времени через единицу площади из жидкости, обозначим q_ж. От чего может зависеть это число? Как уже отмечалось, положение дел в замкнутом сосуде зависит лишь от устанавливаемых извне давления и температуры. Поэтому величина q_ж также должна зависеть только от них:

q_ж = q_ж(p, T).

И совершенно аналогично для пара

q_п = q_п(p, T).

Явный вид этих зависимостей нам неизвестен. Он различен для разных веществ, а мы пытаемся установить общие закономерности. Вода выбрана только в качестве удобного примера, но никаких ее конкретных свойств использовано не будет. Для нашего рассмотрения важно лишь существование зависимостей, а не их явная форма.

Итак, молекулы, покидающие пар, переходят в жидкость, и наоборот. Если

q_ж(p, T) > q_п(p, T),

то паровая фаза будет расти за счет жидкой — преобладает процесс испарения. Если же

q_ж(p, T) < q_п(p, T),

то жидкая фаза будет «съедать» паровую — преимущества за конденсацией. Наконец, когда число молекул в каждой из фаз не меняется со временем, т. е. когда

q_ж(p, T) = q_п(p, T),

жидкая и паровая фазы находятся в равновесии.

На фазовой диаграмме последнему уравнению соответствует линия равновесия жидкость — пар. Если бы явный вид зависимостей q_ж(p, T) и q_п(p, T) был известен, то с помощью этого уравнения можно было бы производить практические расчеты фазовой диаграммы. Например, подставив в уравнение значение нормального атмосферного давления и решив его, получили бы для температуры равновесия значение 100 °С.

Теперь пора ввести новое понятие — число степеней свободы. Так в термодинамике принято называть количество внешних параметров, которые в некоторых пределах можно независимо друг от друга менять, не меняя при этом фазового состояния системы. В изучаемом нами случае внешних параметров всего два — давление и температура. А теперь взгляните еще раз на фазовую диаграмму воды (рис. 2). Каждому однофазному состоянию соответствует некоторая площадь, в пределах которой можно свободно варьировать оба параметра. Например, воду как таковую (жидкую) можно нагреть или приложить к ней внешнее давление, или сделать то и другое одновременно (все это, конечно, в некоторых пределах), и при этом фазовое состояние системы в сосуде не изменится — вода так и останется водой. То же самое справедливо в случае льда или пара. Можно сделать вывод, что однофазная система имеет две степени свободы.

Совсем другая ситуация при двухфазном равновесии. Имеется уравнение, связывающее оба внешних параметра. В случае равновесия жидкость — пар мы его уже записывали: q_ж(p, T) = q_п(p, T). Поэтому свободно менять можно уже только один параметр, а другой надо «подстраивать» к нему в соответствии с уравнением. Если же мы станем менять оба параметра независимо друг от друга, то «соскочим» с линии фазового равновесия и одна из фаз исчезнет — фазовое состояние системы изменится. Поэтому состояние двухфазного равновесия имеет всего одну степень свободы.

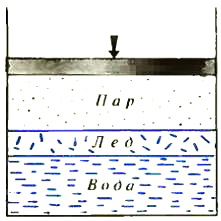
Рис. 3

Перейдем теперь к трехфазному равновесию, добавив к воде и пару лед. Предположим, что фазы в сосуде расположены так, как показано на рисунке 3. Учтем, что число молекул, покидающих за единицу времени через единицу площади лед, также будет функцией давления и температуры — q_л = q_л(p, T), и запишем условие равновесия фаз:

для равновесия пар — лед —

q_п(p, T) = q_л(p, T),

для равновесия лед — вода —

q_ж(p, T) = q_л(p, T).

Легко понять, что аналогичные равенства можно записать для любого взаимного расположения фаз. Обычно их сразу записывают в сокращенной форме

q_п(p, T) = q_л(p, T) = q_ж(p, T).

Решение последней системы из двух уравнений с двумя неизвестными определит то сочетание давления и температуры, при котором в равновесии могут находиться все три фазы. Ясно, что число степеней свободы трехфазного равновесия равно нулю.

Если бы мы стали рассматривать четырехфазное равновесие однокомпонентной системы, уравнений стало бы уже три —

q_I(p, T) = q_II(p, T) = q_III(p, T) = q_IV(p, T),

а неизвестных по-прежнему осталось бы два. Система из трех уравнений с двумя неизвестными в общем случае решения не имеет. Поэтому максимальное число фаз, которые могут находиться в равновесии в однокомпонентной системе, равно трем.

Содержание этих закономерностей и составляет суть правила фаз Гиббса: в однокомпонентной системе число степеней свободы C просто связано с числом фаз Ф, находящихся в равновесии,—

C = 3 - Ф (C > 0).

Рис. 4

Взгляните на три диаграммы состояния однокомпонентной системы, приведенные на рисунке 4. Не вдаваясь в рассмотрение конкретных веществ, для которых они построены, можно сразу утверждать их ошибочность. На первой диаграмме существует точка четырехфазного равновесия. На второй трехфазное равновесие имеет две степени свободы. На третьей — две степени свободы имеет двухфазное равновесие. Говоря словами одного из персонажей А. П. Чехова, «этого не может быть, потому что этого не может быть никогда». Правило фаз категорически запрещает такие ситуации.

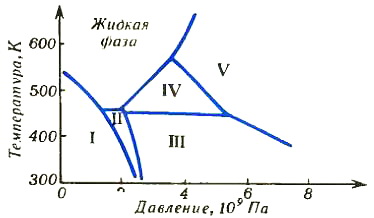
Рис. 5

А теперь посмотрите на рисунок 5, где изображена диаграмма состояния висмута. Римскими цифрами обозначены его пять различных кристаллических фаз. Можете сами убедиться, что несмотря на довольно сложный вид диаграммы, ни один из ее участков не противоречит правилу фаз.

Правило фаз для многокомпонентных систем

Чистая вода, чистый висмут или какое-либо иное чистое вещество встречаются сравнительно редко. Значительно чаще приходится иметь дело с различными многокомпонентными системами. Например, с растворами. Простейший пример раствора — сладкая вода, состоящая из двух компонентов — сахара и воды, каждый из которых представлен своим типом молекул.

Чтобы описать состояние раствора, нужно, помимо температуры и давления, указать относительное содержание всех компонентов, т. е. их концентрации. Понятно, что в системе, состоящей из К компонентов, следует указать значение (К - 1) концентрации.

Для фаз, находящихся в равновесии, температура и давление — общие (одинаковые) параметры. А вот равенство концентраций ниоткуда не следует. Более того, легко привести пример противоположного толка. Если в чай положить слишком много сахара, то он не размешается даже при длительной и интенсивной работе ложечкой. Установится двухфазное равновесие жидкого сладкого чая и лежащего на дне твердого сахара. Понятно, что концентрации компонентов в каждой из двух фаз совершенно различны. Учтя это обстоятельство, попробуем описать ситуацию математически.

Предположим, что в системе из К компонентов в равновесии находятся Ф фаз. Теперь условия равновесия следует записать для каждого компонента :

q⁽¹⁾_I = q⁽¹⁾_II = q⁽¹⁾_III = ... = q⁽¹⁾_Ф,

q⁽²⁾_I = q⁽²⁾_II = q⁽²⁾_III = ... = q⁽²⁾_Ф,

...

q^(K)_I = q^(K)_II = q^(K)_III = ... = q^(K)_Ф

(нижний индекс обозначает номер фазы, а верхний — номер компонента). Эта система равенств является непосредственным обобщением условий равновесия в однокомпонентной системе.

Каждая из величин q должна зависеть от общих давления и температуры — от р и Т — и от (К - 1) концентрации в своей фазе. Таким образом, общее число параметров, которые надо указать, чтобы описать равновесие, равно 2 + (К - 1)Ф. А теперь подсчитаем общее число уравнений в последней системе. Для каждого компонента оно равно (Ф - 1), а всего компонентов К. Итак, получаем К(Ф - 1).

Каждое из уравнений дополнительно связывает между собой параметры, описывающие состояние системы, и тем самым понижает число степеней свободы. Так что в многокомпонентной системе число степеней свободы равно общему числу параметров минус количество уравнений:

С = 2 + (К - 1)Ф - К(Ф - 1) = 2 - Ф + К.

(Для К= 1 (однокомпонентная система) получим уже известное нам равенство С = 3 - Ф).

Поскольку число степеней свободы по смыслу должно быть неотрицательным, из правила фаз сразу следует, что максимальное количество фаз, которые могут находиться в равновесии в К-компонентной системе, равно 2 + К.

Правило фаз выводилось для замкнутой системы. Но, строго говоря, такого почти никогда не бывает. Система обычно находится в контакте с внешней средой, с которой может происходить обмен атомами или молекулами. Иногда с этим приходится считаться. Однако в подавляющем большинстве случаев этим обстоятельством можно безболезненно пренебречь.

Из правила фаз следует очень много интересных выводов. Наверное, вы теперь без труда объясните, почему температура равновесия вода — лед строго фиксирована. Но если мы имеем дело не с чистой водой, а с каким- нибудь водным раствором, то равновесие вода — лед (не чистые!) при фиксированном внешнем давлении «захватит» целый диапазон температур. Почему это так, постарайтесь объяснить сами на основании правила фаз. Еще один пример того же рода: чистые металлы плавятся при фиксированных температурах, а их сплавы — в некотором температурном интервале. В частности, чистая медь плавится при 1083 °С. А сплав, состоящий на 95 % из меди и на оставшиеся 5 % из мышьяка, плавится (т. е. существует в виде смеси жидкого расплава и кристалла) от 800 до 1050 °С.

* * *

На примере правила фаз можно понять исключительные возможности, которые предоставляет исследователю теория. Не используя практически никакой информации о конкретных веществах, нам удалось узнать некоторые общие закономерности фазовых превращений. А это интересно не только для физиков. Фазовые превращения имеют огромное значение с точки зрения практики. Вызывая или, наоборот, тормозя их, можно управлять свойствами вещества.

Арсенал орудий труда у Гиббса был очень скромный — перо да бумага. Но ими он сумел сделать немало. Здесь уместно вспомнить крылатые слова Людвига Больцмана: «Нет ничего практичнее хорошей теории». На рубеже XIX и XX веков абстрактные идеи Гиббса о равновесиях в сложных системах (в том числе и правило фаз) были восприняты широким кругом ученых и инженеров и материализовались в промышленных процессах химии и металлургии. Происходило это бурно, иногда драматично. Но... это уже другой рассказ.

Примечания

1. ↑ Сосуд можно помещать в электрическое поле, в магнитное, но эти случаи в дальнейшем рассматриваться не будут.

2. ↑ В жидкой (да и в газообразной) фазе существует гидростатическое давление, но мы будем вести разговор о ситуации, когда оно много меньше общего для системы давления р.

3. ↑ Хотя вода состоит из водорода и кислорода, это — пример однокомпонентной системы, так как элементы находятся в соединенном состоянии (молекулы Н₂О).

4. Твёрдые растворы. Фаза. Фазовая диаграмма.

5. Фазой называется часть или совокупность гомогенных частей системы, разделённых границами раздела, обладающие одинаковым составом, структурой, свойствами и при переходе через границу раздела структуры, состав, свойства или структура могут меняться скачкообразно.

6. Графическим способом описания фаз, находящихся в состоянии равновесия, является диаграмма состояния.

7. Твёрдыми растворами называются фазы переменного состава, в которых атомы одного из компонентов образуют кристаллическую решётку, в которой располагаются атомы другого компонента.

8. Твёрдые растворы

9. По способу расположения атомов второго компонента в решётке растворителя подразделяют на :

10. А). Твёрдые растворы типа замещения

11. Б). Типа внедрения

12. В). Типа вычитания.

13. Юм - Розери сформулировал ряд правил для образования твёрдых растворов типа замещения:

14. 1). Размерный фактор. Размеры атомов сплавляемых компонентов не должны различаться более, чем на 10-15%. Например:

15. Ag-Au dr=0.2% ГЦК; Ni-Cu r=2.7% ГЦК; V-Ti r = 2% ОЦК

16. 2). Структурный фактор.

17. Решётки атомов растворителя и растворимого вещества должны быть изоморфны, т.е. структурно подобны.

18. 3). Валентный фактор.

19. А). Атомы должны принадлежать к одному или соседним столбцам в таблице Менделеева, т.е. иметь валентность почти одинаковую.

20. Б). Атомы растворимого вещества должны быть гораздо меньше атомов растворителя (>15%).

21. Внедряющиеся атомы: N, H, C, ...

22. В). Определяется электронным фактором и в данном курсе не обсуждается.

23. Для характеристики состояния сплава необходимо знать число фаз и их концентрацию.

24. Для твёрдого раствора типа внедрения характерна только ограниченная растворимость. Это обусловлено тем, что размеры атомов сплавляемых компонентов различны, вследствие этого атомы сплавляемых компонентов располагаются в ограниченных объёмах кристаллах, называемых пустотами.

25. Различаются тетра и октапустоты.

26. Для примера рассмотрим ячейки ГЦК и ОЦК.

27. ГЦК октапустоты - одна пустота находится в центре куба. Её вершинами являются атомы, расположенные в гранях куба и, кроме того, если построить соседние ячейки, то можно заметить, что центры других октопустот будут находиться в середине рёбер куба. Рёбер в кубе 12 и каждое ребро принадлежит 4 ячейкам. Таким образом, у нас есть одна пустота, принадлежащая только одной ячейке и 12 пустот, принадлежащих данной ячейке на одну четверть. Следовательно на одну ячейку приходится 1+12/4 = 4 октапустоты. Тетрапустота образована тремя атомами, находящимися в центрах соседних граней и вершиной куба.. Так как вершин в кубе 8 и из каждой вершины мы можем построить только одну тетрапустоту, то тетрапустот у нас – 8. Размер октапустоты – 0,41R, где R это радиус атома растворителя, а размер тетрапустоты – 0,22R. (рис. 16)

28.

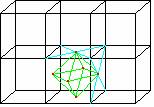
29. рис. 16. Расположение тетра и октапустот в ГЦК решётке.

30. Для ОЦК решётки расчёт предлагается студентам, в качестве практического задания

31. Поскольку число пустот ограничено и размеры их малы по сравнению с размерами атомов, то очевидно, что растворимость может быть только ограниченной.

32. Отличие твёрдых растворов от химических соединений:

33. 1). Химическое соединение образуется при простом кратном соотношении компонент. A_nB_m, где n и m простые целые числа. Т_плавл химического соединения постоянна. При образовании химического соединения наблюдаются значительные тепловые дефекты.

34. 2).Свойства химического соединения резко отличаются от свойств образовавших их компонентов.

35. Фазы. Фазовая диаграмма.

36. Во многих случаях давление (за исключением очень высокого), практически не влияет на фазовое равновесие в сплавах в жидком и твёрдом состояниях, поэтому диаграмма состояния строится в осях T⁰, C,%.

37. Фазовые диаграммы бывают двух типов растворимости: неограниченная и ограниченная.

38. Неограниченная растворимость характерна для твёрдого раствора типа замещения. Чтобы охарактеризовать образовавшиеся фазы, нужно определить их количественное содержание и их число.

39. Существует правило рычага для описания количества твёрдых фаз в образце.

40. Для описания числа степеней свободы используется правило фаз Гиббса.

41. Правило фаз Гиббса. Число степеней свободы. С=К-Ф+1;

42. С – число степеней свободы,

43. К – число компонент,

44. Ф – число фаз.

45. Для примера можно рассмотреть H₂0 при 0 ⁰С. У нас одна компонента: H₂0. При температуре 0 ⁰С у нас существует две фазы: твёрдая (лёд) и жидкая (вода). С=1+1-Ф. Так как у нас фаз две, то число степеней свободы равно 0 и, следовательно, температура, при которой у нас существует две фазы остаётся постоянной 0 ⁰С.

46. В качестве примера можно взять диаграмму состояний железо – углерод (рис.17).

47. Рассмотрим характеристики компонентов, из которых образуются сталь и чугун.

48. Вначале дадим характеристику компонентов железа и углерода.

49. Железо - полиморфно (может находиться в различных кристаллографических модификациях).

50. Порядковый номер железа в таблице Менделеева – 26, атомная масса - A= 55,85 а.е.м. (атомные единицы массы). Радиус атома - R = 1,27А. Температура плавления - Т_пл = 1539⁰С. Плотность – 7,68 г/см³

51. кривая охлаждения железа (рис. 18).

52.

53.

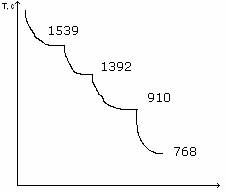
54. рис.18. Кривая охлаждения железа

55.

56. 768⁰С – точка Кюри (магнитное превращение, в котором α –Fe из ферромагнитного состояния переходит в парамагнитное.)

57. 910⁰С – температура, при которой α –Fe переходит в γ Fe с решёткой ГЦК и периодом элементарной ячейки а=3,645 А

58. 1392⁰С – температура, при которой γ Fe переходит в δ Fe с решёткой ОЦК и периодом элементарной ячейки а=2,86068А

59. 1539⁰С – Т_плавл.

60. Углерод полиморфен. Он образует 2 фазы: графит и метастабильную фазу – алмаз. Кроме того на диаграмме присутствует Fe₃C – цементит. Это устойчивое соединение, промежуточная фаза.

61. Углерод, порядковый номер – 12, Неметалл, принадлежит 4 группе 2-го периода в таблице Менделеева, порядковый номер – 6, Т_плавл – 3500⁰С, r – 0,77А, плотность - 2,62 г/см³

62.

63. Диаграмма сплавов железа с углеродом (рис. 17).

64.

65.

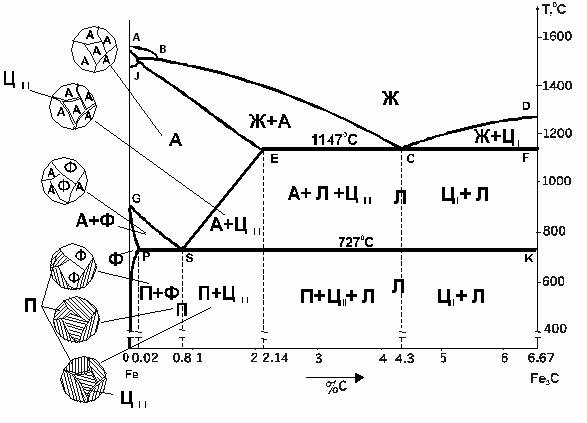
66. рис. 17. Фазовая диаграмма железо – углерод.

67. Ж - жидкий сплав, А – аустенит, П – перлит, ЦI – первичный цементит, ЦII – вторичный цементит, Л – ледебурит.

68.

69. Рассмотрим некоторые основные линии и точки, обозначенные на диаграмме.

70. А – точка плавления;

71. Ликвидусом называется кривая, на которой начинается кристаллизация, а солидусом – кривая, на которой кристаллизация заканчивается. Соответственно:

72. ABCD- кривая ликвидуса, HGECF – кривая солидуса

73. PSK и ECF – соответствуют нонвариантному превращению (Это такие прямые, при которых постоянные температура и состав).

74. Рассмотрим точку C: По правилу фаз Гиббса число степеней свободы равно 0, так как из жидкого раствора одновременно кристаллизуются аустенит и цементит и, следовательно, превращение происходит при постоянных составе и температуре. Эта температура называется температурой эвтектики. Эвтектика – механическая смесь фаз, обусловленная кристаллизацией двух фаз из жидкой фазы. На диаграмме состояния Fe-C эвтектика соответствует точке C.

75. B точке S одновременно происходит кристаллизация двух фаз (феррита и цементита) из твёрдой фазы аустенита. Эта точка называется эвтектоид.

76. На диаграмме состояний можно выделить два твёрдых раствора – это феррит, он представляет собой твёрдый раствор углерода в решётке α-Fe (углерод размещается вдоль рёбер), а твёрдый раствор в решётке γ-Fe – аустенит.

77. Механическая смесь Феррит + цементит называется перлитом. (эвтектоид)

78. Аустенит + цементит – ледебурит. (эвтектика) (имеет характерную леопардовую окраску).

79. Посмотрим на точку Е: это точка предельной растворимости углерода в аустените, при температуре эвтектического превращения. Кривая EF – кривая предельной растворимости углерода в аустените.

80. Точка P соответствует точке предельной растворимости углерода в феррите.

81. Сталь – сплав железа с углеродом с содержанием углерода до 2,14%.

82. По содержанию углерода стали различают:

83. - доэвтектоидные, (от 0,02% до 0,81% содержания углерода)

84. - эвтектоидные, от (0,81% содержания углерода)

85. - заэвтектоидные. (от 0,81% до 2,14% содержания углерода)

86. Структура сталей представлена:

87. - феррит и перлит,

88. Феррит представляет собой зёрна белого цвета, а перлит – чёрного.

89. - Различают пластинчатый и зернистый феррит.

90. Точка Q – 0,02% - техническое железо.

91. 0,81%С - перлит (эфтектоидная сталь)

92. При содержании углерода от 2,14% до 6,67% образуются чугуны. По содержанию углерода они подразделяются на:

93. - доэвтектические

94. Они представлены смесью перлит + цементит + ледебурит, и от 2,14% до 4,3% содержания углерода

95. - эвтектические

96. Они представлены ледебуриом, и содержат 4,3% углерода

97. - заэвтектические

98. Они представлены смесью цементит + ледебурит и содержат от 4,3% до 6,67% углерода.

99. Свойства чугунов зависят от вида и формы включения углерода в железо.

100. Классы чугунов представлены на рис 19.

101.

102.

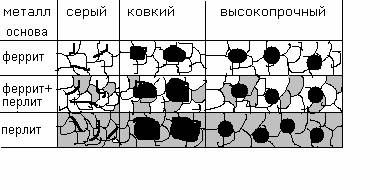
103. рис.19. Классы чугунов.