Элементы вариационного исчисления

Пример 1 (задача о брахистохроне)

Исторически первой задачей о вариационном исчислении была задача о брахистохроне, поставленная И.Бернулли: среди всех кривых, соединяющих две данные точки плоскости, найти ту, двигаясь по которой под действием силы тяжести, материальная точка попадает из начальной точки в конечную за кротчайшее время (рис. 1). Кривая, вдоль которой тело, скорее всего скатывается из начальной точки в конечную, называется брахистохроной.

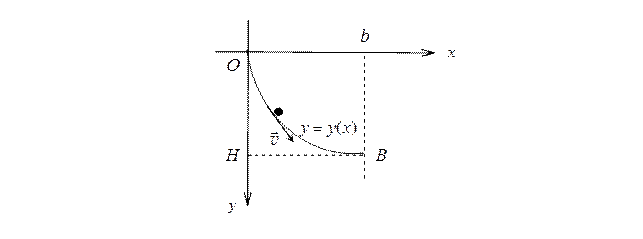Рис. 1.

Построим математическую модель задачи. Введем систему координат, начало которой совместим с точкой . Представим искомую кривую уравнением , . Применим закон сохранения энергии, трением и сопротивлением среды пренебрегаем

,

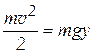где 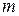– масса тела, 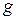– ускорение свободного падения, 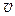– величина скорости.

Если 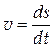, где, 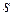– путь, пройденный телом, то 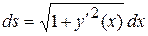, 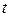– время движения.

Тогда

.

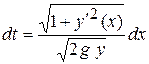Полное время движения из точки 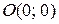в точку 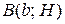выражается интегралом

.

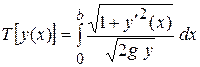Искомая кривая 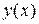должна удовлетворять условию

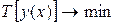
и условиям

, .

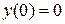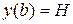Определение. Переменная величина 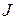называется функционалом, зависящим от функций 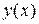, принадлежащих некоторому классу функций 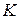, если каждой функции 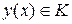, согласно некоторому правилу, соответствует единственное число, которое записывается

.

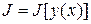Таким образом, функционал – это отображение

.

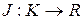Класс функций 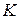, на котором определен функционал называется областью определения функционала и обозначается 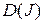, а множество 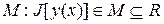называется множеством значений функционала .

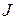Пример 2 (цепная линия)

Найдём форму, какую принимает тонкая гибкая однородная нить (цепь) длины 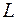под действием силы тяжести.

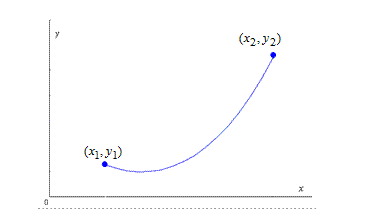
Рис. 2.

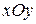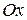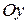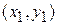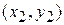Пусть система выбрана так, что ось горизонтальна, ось направлена вертикально вверх, а координаты точек подвеса суть и (рис.2). Пусть далее, 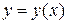задаёт линию, занимаемую цепью. Из механики известно, что получающаяся форма цепи 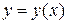соответствует экстремуму её потенциальной энергии

,

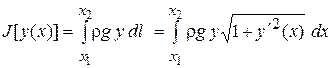где 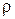– плотность материала цепи, 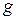– ускорение свободного падения.

Искомая форма цепи 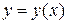должна удовлетворять условию

,

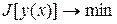краевым условиям

, ,

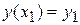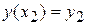и условию, определяющему длины цепи

.

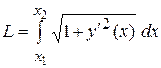Приведенные примеры относятся к задаче на минимум функционала вида

,

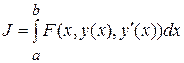который часто встречается в практических приложениях.

Вариационное исчисление занимается условиями существования экстремума и методами их нахождения.

Обозначим через 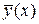некоторую фиксированную функцию из области определения функционала .

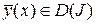Разность

,

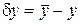называют вариацией аргумента функционала .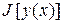

Вариация функции 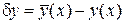является функцией 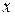. Эту функцию можно дифференцировать несколько раз, причем, нетрудно видеть что

.

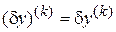Приращением функционала, отвечающим приращению аргумента 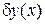, называется величина

,

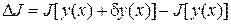где , , .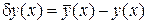

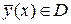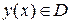Если 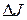может быть представлено в виде

,

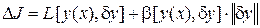где 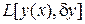– линейный (и, стало быть, ограниченный) функционал относительно 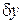, а функционал 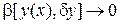при норме 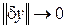, то L называют вариацией функционала 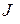и обозначают

.

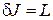Для 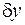нормой можно взять

.

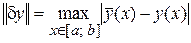Формально, существование вариации функционала связывают с условием его дифференцируемости

.

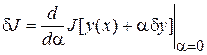Пример. Найдем вариацию функционала .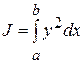

Имеем .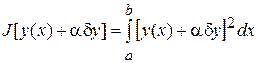

Тогда ,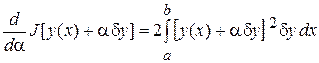

и, следовательно .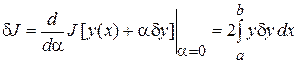

Для функционала

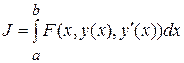
найдем первую вариацию.

,

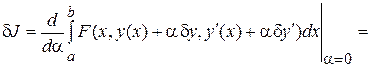
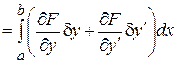или

.

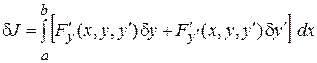Теорема. Если функционал 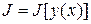, определенный на 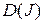имеющий вариацию, достигает экстремума на функции 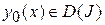, то

.

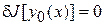Рассмотрим функционал

,

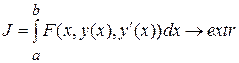с заданными граничными условиями: , .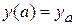

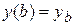Предположим, данный функционал достигает экстремум в точке 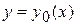. Тогда, согласно необходимому условию существования экстремума

.

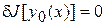В найденной вариации 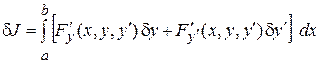проинтегрируем второе слагаемое по частям:

.

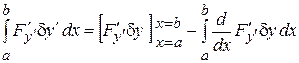С учетом услови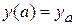й и 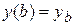, имеем 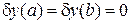, и получаем

.

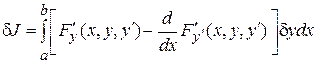Согласно необходимому условию существования экстремума

.

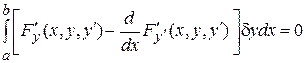В этом выражении вариация 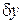является произвольной непрерывной функцией на 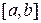, так что получаем

.

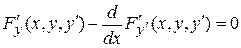Полученное дифференциальное уравнение называется уравнением Эйлера для функционала .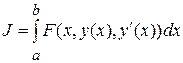

Таким образом, условие существования экстремума функционала 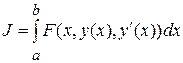при условиях 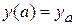, 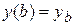приводит к краевой задаче для дифференциального уравнения 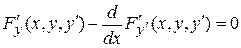при тех же условиях , .

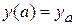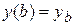Любое решение задачи

,

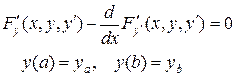называется экстремалью.

Если в уравнении 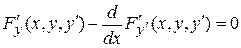раскрыть производную, то получим краевую задачу

.

.
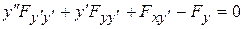
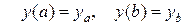