Тензорная природа характеристических свойств распределения нагрузок приёмников
В задачах проектирования систем промышленного электроснабжения, в которых приёмники электроэнергии рассматривают как точки, характеризующиеся удельными приведёнными затратами на элементы системы электроснабжения, активными и реактивными нагрузками, координатами мест расположения и другими параметрами, свойства распределения этих величин имеют тензорную природу и с наибольшей полнотой могут быть описаны тензорами[2]. Тензор является обобщенным понятием вектора как физической величины, которая в каждой точке характеризуется числом и направлением. В отличие от вектора тензор как физическая величина в каждой точке по каждому направлению характеризуется своим числовым значением.
При изучении разброса нагрузок относительно точки ( 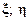 ) мы воспользовались тензором, состоящим из трёх компонент
) мы воспользовались тензором, состоящим из трёх компонент
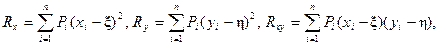 (30)
(30)
который в каждых двух взаимно перпендикулярных направлениях, фиксированных осями координат, описывает разбросы нагрузок и связи распределения нагрузок относительно этих осей. Аналитическим признаком тензора являются формулы преобразований его компонент при повороте системы координат на угол 
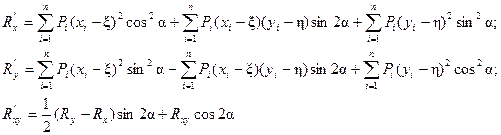 (31)
(31)
По этим формулам по каждым двум взаимно перпендикулярным направлениям могут быть вычислены показатели разброса нагрузок и момент их связи. Эти показатели допускают и другую геометрическую интерпретацию.
В системе координат 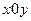 рассмотрим линию, определённую радиусом - вектором
рассмотрим линию, определённую радиусом - вектором 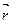 с координатами (
с координатами ( 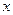 ;
; 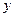 ).
).
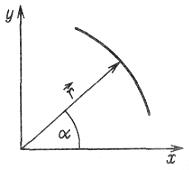
Рис. 4. Линия, определённая радиусом - вектором 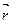 , использованная для вывода уравнения эллипса
, использованная для вывода уравнения эллипса
Из рис. 4 следует, что
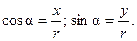 (32)
(32)
Внесём, например, во второе равенство (31) вместо тригонометрических функций их выражения через координаты ( 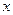 ;
; 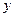 ) и длину радиуса - вектора
) и длину радиуса - вектора 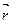 рассматриваемой линии из (32), будем иметь:
рассматриваемой линии из (32), будем иметь:
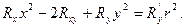 (33)
(33)
Если положить, что 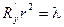 – величина постоянная, то полученное уравнение определяет линию 2-го порядка. Поскольку величины
– величина постоянная, то полученное уравнение определяет линию 2-го порядка. Поскольку величины 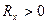 и
и 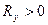 положительны по определению, то эта линия является эллипсом рассматриваемого тензора. Эллипс несёт существенную информацию о распределении нагрузок в группе и об их разбросах относительно его центра и главных осей. Эта информация раскрывается при помощи инвариантов тензора – величин, не зависящих от выбора системы координат. Тензор (30) имеет два независимых инварианта, при помощи которых можно построить любое число других инвариантов, описывающих характеристические свойства распределения нагрузок в изучаемой группе приёмников. В качестве независимых инвариантов тензора выбирают два инварианта
положительны по определению, то эта линия является эллипсом рассматриваемого тензора. Эллипс несёт существенную информацию о распределении нагрузок в группе и об их разбросах относительно его центра и главных осей. Эта информация раскрывается при помощи инвариантов тензора – величин, не зависящих от выбора системы координат. Тензор (30) имеет два независимых инварианта, при помощи которых можно построить любое число других инвариантов, описывающих характеристические свойства распределения нагрузок в изучаемой группе приёмников. В качестве независимых инвариантов тензора выбирают два инварианта
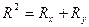 (34)
(34)
и
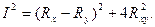 (35)
(35)
