Раздел (Разложение функций в степенной ряд. Применение рядов)
1 Найти коэффициент при x4 в разложении функции y=cos2( 
) в ряд Маклорена.
A. 
2 Найти коэффициент при x2 в разложении функции y=3+e - 2x в ряд Маклорена.
A. 2
3 Найти коэффициент при x3 в разложении функции y=2- e 2x в ряд Маклорена.
A. 
коэффициент при x2 в разложении функции y= cos ( ) в ряд Маклорена.
A. - 
5 Найти коэффициент при x2 в разложении функции y= sin(2x) в ряд Маклорена.
A. 0
6 Найти коэффициент при x2 в разложении функции y= e 3x в ряд Маклорена.
A. 
7 Найти коэффициент при x2 в разложении функции y= (1- x)℮x в ряд Маклорена.
A. - 
8 Найти коэффициент при x3 в разложении функции y= sin2 в ряд Маклорена.
A. 0
9 Найти коэффициент при x2 в разложении функции y= 
в ряд Маклорена.
A. 
10 Найти коэффициент при x2 в разложении функции y= 
в ряд Маклорена.
A. 
11 Найти коэффициент при x4 в разложении функции y= cos2(x) в ряд Маклорена.
A. 
12 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,86
13 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,74
14 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,94
15 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 1,61
16 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,10
17 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,45
18 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,12
19 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,16
20 Вычислить определенный интеграл 
с точностью до 0,01, разложив подынтегральную функцию в степенной ряд.
A. 0,31
21 Найти коэффициент при x2 в разложении в степенной ряд частного решения дифференциального уравнения y'=sinx+y2 с начальным условием y(0)=1
A. 
21 Найти коэффициент при x2 в разложении в степенной ряд частного решения дифференциального уравнения y'=x2+ 
с начальным условием y(0)=1
A.
22 Найти коэффициент при x2 в разложении в степенной ряд частного решения дифференциального уравнения y'=2ey -xy с начальным условием y(0)=0
A. 2
23 Найти коэффициент при x2 в разложении в степенной ряд частного решения дифференциального уравнения y'=x2+ y2 с начальным условием y(0)=1
A. 1
24 Найти коэффициент при x2 в разложении в степенной ряд функции 
A. 
25 Найти коэффициент при x3 в разложении в степенной ряд 
A.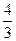 
1. Какова фундаментальная система решений линейного однородного уравнения второго порядка с постоянными коэффициентами в случае различных корней 
и 
характеристического уравнения?
A) 
, 
;
2. Какова фундаментальная система решений линейного однородного уравнения второго порядка с постоянными коэффициентами в случае равных корней = характеристического уравнения?
A) , 
;
3. Какова фундаментальная система решений линейного однородного уравнения второго порядка с постоянными коэффициентами в случае комплексно сопряженных корней 
характеристического уравнения?
A) 
, 
;
4. Пусть правая часть линейного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид 
и число 
является простым корнем соответствующего характеристического уравнения. Тогда частное решение этого уравнения имеет вид 
, где
A) 
; B) 
; C) 
; D) 
; E) 
.
5. Укажите характеристическое уравнение дифференциального уравнения
C) к2+рк+q=0;
Раздел 1
| 1. А | 6. А | 11. А | 16. А | 21. А |
| 2. В | 7. В | 12. В | 17. С | 22. С |
| 3. С | 8. С | 13. С | 18. В | 23. В |
| 4. D | 9. D | 14. D | 19. D | 24. D |
| 5. E | 10.Е | 15. Е | 20. Е | 25. А |
Раздел 2
| 1. В | 6. А | 11. А | 16. В | 21. С |
| 2. Е | 7. В | 12. В | 17. С | 22. В |
| 3. А | 8. С | 13. Е | 18. D | 23. D |
| 4. В | 9. D | 14. D | 19. А | 24. А |
| 5. E | 10.С | 15. А | 20. Е | 25. Е |
Раздел 3
| 1. А | 2. А | 3. А | 4. А | 5. С |
1.Переход к полярным координатам в двойных и цилиндрическим в тройных интегралах
1 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где 
.
A) 32 
2 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где .
A) 8
3 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где .
A) 
4 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где 
2
5 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где
A) 
6 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где
A) 
7 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где
A) 
8 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где
A) 
9 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где 
A)
10 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где
A) 
11 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где
A) 16
12 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где
A) 24
13 С помощью перехода к полярным координатам, вычислить двойной интеграл: 
, где
A) 
14 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где 
.
A)
15 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где 
A) 6
16 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где
A) 12
17 С помощью перехода к цилиндрическим координатам вычислить тройной интеграл: 
, где
A) 2
18 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где 
.
A) 
19 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где .
A) 
20 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где 
A) 
21 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: 
, где 
A) 
22 С помощью перехода к цилиндрическим координатам, вычислить тройной интеграл: , где 
A) 4
23 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где D-часть круга , лежащая в верхней полуплоскости
A) 16
24 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где D-часть круга , лежащая в верхней полуплоскости
A) 4
25 С помощью перехода к полярным координатам, вычислить двойной интеграл: , где D-часть круга , лежащая в верхней полуплоскости
A) 
1. Процесс нахождения решений дифференциального уравнения называется …
A) Дифференцированием
B) Интегрированием
C) Логарифмированием
D) Потенцированием
E) Разделением переменных
2. Если в дифференциальном уравнении неизвестная функция является функцией одной независимой переменной, то дифференциальное уравнение называется …
A) Уравнением в частных производных
B) В полных дифференциалах
C) Однородным
D) Обыкновенным
E) Линейным
3. Наибольший порядок, входящей в дифференциальное уравнение производной неизвестной функции определяет его …
A) Степень
B) Тип
C) Порядок
D) Показатель
E) Номер
4. Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной. Такое линейное уравнение имеет вид:
A) 
5. К какому типу дифференциальных уравнений приводятся однородные дифференциальные уравнения первого порядка:
С разделяющимися переменными
6. Если в однородном дифференциальном уравнении 
- однородные функции четвертого измерения, то их частное - ...
A) Нулевого измерения
7. Среди дифференциальных уравнений первого порядка определите линейное
A) 
8. 
- это дифференциальное уравнение
С разделяющимися переменными
9. Для решения уранения вида 
используется
A) Подстановка 
10. Для решения уравнения вида 
используется
A) Подстановка
11. Для решения уравнения вида 
используется
A) Двойное интегрирование
12. Дифференциальное уравнение первого порядка 
, где - дифференцируемые функции является уравнением в полных дифференциалах, если
A) 
13. Определите порядок дифференциального уравнения 
A) 1
14. Определите порядок дифференциального уравнения 
A) 5
15. Определите порядок дифференциального уравнения 
A) 2
ТЕСТЫ ПО ТЕОРИИ ВЕРОЯТНОСТИ
1. Если 
число всех единственно возможных и равновозможных элементарных исходов испытания, а 
число благоприятствующих событию 
исходов, то вероятность события определяется формулой:
A) 
2.Вероятность достоверного события равна:
A) 1
3.Вероятность невозможного события равна:
A) 0
4.Вероятность любого события 
есть положительное число, удовлетворяющее неравенству:
A) 
5Вероятность появления одного из двух несовместных событий А или В, безразлично какого, равна:
A) 
6Вероятности противоположных событий 
и 
удовлетворяют условию:
7Вероятность совместного появления двух зависимых событий А и В равна:
A) 
8Вероятность появления хотя бы одного из двух совместных событий и 
равна
A) 
9Указать формулу полной вероятности Р(А), если В1 ,В2,…,Вn - гипотезы :
A) 
10Сумма вероятностей событий 
образующих полную группу, равна
A) 1
11Математическое ожидание М(Х) числа появлений события в 
независимых испытаниях, в каждом из которых вероятность 
появления события постоянно, равна
A) 
12Дисперсией D(X) дискретной случайной величины Х называют
A) 
13Число размещений из n различных элементов по k без повторений определяется по формуле
A) 
Ответ
14Сумма вероятностей противоположных событий равна
A) 1
15Дисперсия D(X) постоянной величины 
равна
A) 
16Дисперсия D(X) числа появлений события в независимых испытаниях, в каждом из которых вероятность появления события постоянно, равна
A) 
, где 
17Число перестановок из n различных элементов без повторений определяется по формуле
A) 
Ответ
18 Число сочетаний из n различных элементов по k без повторений определяется по формуле
A) 
B) 
C) 
D) 
E) 
19Если A – случайное событие, то 
A) 
20Если A – достоверное событие, то 
A) 1
21Если 
-число вариант, меньших х; - объем выборки, то эмпирическая функция распределения 
определяется равенством
A) 
23Два события образуют полную группу, если они:
A) противоположные
24 Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р, событие наступит ровно k раз находится по формуле Бернулли:
A) 
Ответ
25 Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р, событие наступит менее k раз:
A) 
B) 
C) 
D) 
E) 
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1. Ряд называется сходящимся, если
С) сущесвует конечный предел частичной суммы
2. Ряд называется расходящимся, если
С) предел частичной суммы не существует
3 Если ряд сходящийся, то
D) предел n – ного члена стремится к нулю при 
4 Какое условие является достаточным для расходимости ряда 
?
В) 
5 Положительный ряд является сходящимся, если
А) 
6 Положительный ряд является расходящимся, если
В) 
7. Положительный ряд является сходящимся, если
С) 
8 Положительный ряд является расходящимся, если
С) 
9 Положительный ряд будет сходящимся, если при сравнении со сходящимся положительным рядом 
выполняется условие:
D) 
10. Положительный ряд будет расходящимся, если при сравнении с расходящимся положительным рядом выполняется условие:
С) 
11 Положительный ряд будет сходящимся, если при сравнении со сходящимся положительным рядом выполняется условие:
А) 
(С¹0)
12 Положительный ряд 
будет расходящимся, если при сравнении с расходящимся положительным рядом 
выполняется условие:
D) (С¹0)
13 Какое условие является достаточным для сходимости ряда 
?
Е) 
14. Какое условие является достаточным для расходимости ряда 
?
D) 
15 Члены ряда 
положительны и не возрастают, и f(x) – такая непрерывная невозрастающая функция, что 
. Тогда если несобственный интеграл 
сходится, то D)ряд сходится
Теоретические вопросы
1 Если тело 
в форме параллелепипеда, то объем вычисляется по формуле:
A) 
2 Укажите основное свойство двойных интегралов:
A) 
3 Укажите основное свойство двойных интегралов:
A) 
4 Если 
плотность тела 
, масса вычисляется по формуле:
A) 
5 Если тело задано, укажите формулу приведения к повторным интегралам тройного интеграла 
:
A) 
6 Если 
плотность пластинки 
, масса вычисляется по формуле:
A) 
7 Объем цилиндрического тела Т, ограниченного сверху непрерывной поверхностью 
и 
в области 
, снизу областью плоскости Оху, сбоку цилиндрической поверхностью с образующими, параллельными оси Оz вычисляется с помощью двойного интеграла по формуле :
A) 
8 Объем тела вычисляется по формуле:
A) 
9 Если область , функции 
и 
непрерывные на 
, двойной интеграл 
приводится к повторным интегралам:
A) 
10 Площадь области вычисляется по формуле:
A) 
11 Указать в двойных интегралах формулу перехода к полярным координатам: 
.
A) 
12 Площадь области в полярных координатах вычисляется по формуле:
A) 
1. Процесс нахождения решений дифференциального уравнения называется …
F) Интегрированием
2. Если в дифференциальном уравнении неизвестная функция является функцией одной независимой переменной, то дифференциальное уравнение называется …
F) Обыкновенным
3. Наибольший порядок, входящей в дифференциальное уравнение производной неизвестной функции определяет его …
F) Порядок
4. Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной. Такое линейное уравнение имеет вид:
B)
5. К какому типу дифференциальных уравнений приводятся однородные дифференциальные уравнения первого порядка:
С разделяющимися переменными
6. Если в однородном дифференциальном уравнении - однородные функции четвертого измерения, то их частное - ...
B) Нулевого измерения
7. Среди дифференциальных уравнений первого порядка определите линейное
B)
8. - это дифференциальное уравнение
A) С разделяющимися переменными
9. Для решения уранения вида используется
B) Подстановка
10. Для решения уравнения вида используется
B) Подстановка
11. Для решения уравнения вида используется
B) Двойное интегрирование
12. Дифференциальное уравнение первого порядка , где - дифференцируемые функции является уравнением в полных дифференциалах, если
B)
C)
13. Определите порядок дифференциального уравнения
B) 1
14. Определите порядок дифференциального уравнения
B) 5
15. Определите порядок дифференциального уравнения
B) 2
ТЕСТЫ ПО ТЕОРИИ ВЕРОЯТНОСТИ
Теоретические вопросы
1.
Если число всех единственно возможных и равновозможных элементарных исходов испытания, а число благоприятствующих событию исходов, то вероятность события определяется формулой:
A) 
2.
Вероятность достоверного события равна:
A) 1
3.
Вероятность невозможного события равна:
A) 0
4.
Вероятность любого события 
есть положительное число, удовлетворяющее неравенству:
B) 
Вероятность появления одного из двух несовместных событий А или В, безразлично какого, равна:
A) 
.
Вероятности противоположных событий и 
удовлетворяют условию:
A) 
Вероятность совместного появления двух зависимых событий А и В равна:
A) 
Вероятность появления хотя бы одного из двух совместных событий и равна
A) 
Указать формулу полной вероятности Р(А), если В1 ,В2,…,Вn - гипотезы :
A) 
Сумма вероятностей событий образующих полную группу, равна
A) 1
Математическое ожидание М(Х) числа появлений события в независимых испытаниях, в каждом из которых вероятность появления события постоянно, равна
A) 
Дисперсией D(X) дискретной случайной величины Х называют
A) 
Число размещений из n различных элементов по k без повторений определяется по формуле
B) 
Ответ
Сумма вероятностей противоположных событий равна
A) 1
Дисперсия D(X) постоянной величины равна
A) 
Дисперсия D(X) числа появлений события в независимых испытаниях, в каждом из которых вероятность появления события постоянно, равна
A) 
, где 
Число перестановок из n различных элементов без повторений определяется по формуле
A) Ответ
18 Число сочетаний из n различных элементов по k без повторений определяется по формуле
A) 
Если A – случайное событие, то
A) 
Если A – достоверное событие, то
A) 1
Если -число вариант, меньших х; - объем выборки, то эмпирическая функция распределения определяется равенством
A) 
Если 
- варианта выборки, 
- объем выборки, то генеральная средняя 
вычисляется по формуле
A) 
если все объекты генеральной совокупности объема N имеют различное значения признака, равны 
.
Два события образуют полную группу, если они: