Закон распределения дискретной случайной величины

Классическое определение вероятности

Р = т/п . где m -число благоприятствующих событию A исходов, n -число всехэлементарных равновозможных исходов.

1.Теорема сложения вероятностей несовместных событий Р(А + В) .

Теорема сложения вероятностей несовместных событий:

P ( A +B )= P ( A)+P (B)

Теорема сложения вероятностей совместных событий: P ( A + B )= P ( A)+ P (B )− P ( AB)

2.Теорема умножения вероятностей независимы событий Р(А • В) .

Теорема умножения вероятностей независимых событий:

P ( A *B )= P ( A) P (B)

Теорема умножения вероятностей зависимых событий:

P ( A *B )= P ( A) P (B | A),

P ( A *B )= P (B ) P ( A | B).

P ( A | B).- Условная вероятность события А при условии, что произошло событие В.

P (B | A) - Условная вероятность события B при условии, что произошло событие A.

Полная группа событий.

События образуют полную группу если в результате испытаний появл. Хотя бы одно из этих событий.

Противоположные события

Р(А) + Р(-А)=1.

Вероятность появления хотя бы одного события

Вероятность появления хотя бы одного из событий А1 , А2 , ..., Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий Р(А) =1— qⁿ .

6.Формулы комбинаторики С_n^k, А_n^m, т!

а)перестановка P_n=m!=1*2*3…(n-1)*n

б)размещение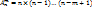

в)сочетание

Задачи на формулу

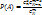
Формула полной вероятности

Р(А) = Р(В )Р (А) + Р(В₂)Р (А) + ...

+ Р(В )Р (А).

P ( A) ⁿ∑_k=1P (H _k )P ( A | H_k ) ,

где H ₁, H ₂,..., H_n -полная группа гипотез,то есть H i* H j =пустое множество, i ≠ j , H i = Ω,Ω-достоверное событие.

Формула Байеса (формула Бейеса).

P_a (B_i)=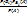

Формула Бернулли

P_n (k)=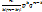

Локальная теорема Лапласа

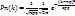
17. Интегральная теорема Лапласа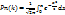

Вероятность наступления события k раз в п испытаниях

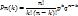
Вероятность наступления менее k раз в n испытаниях

Р_n (0) + Р_n (1) +... + Р_n (k —1) .

13. Вероятность наступления события более k раз в n испытаниях Р_n(k+1)+Р_n (k+2)+...+Р_n (п).

Вероятность наступления события не менее k раз в n испытаниях

Р _n (k) + Р_n (k+1)+... + Р_n (n)

Вероятность наступления события не более k раз в п испытаниях

Р _n (0) + Р_n (1)+... + Р_n (k)

19. Наивероятнейшее число появлений событий в независимых испытаниях (р= const).

Наивероятнейшее число k₀ появления события при n независимых испытаниях:

np −(1− p )≤ k ₀ np  p, p -вероятность появления события при одном испытании.

Закон распределения дискретной случайной величины.

Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения. Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.