Лекция 14. СТАТИСТИЧЕСКОЕ И ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ВЫБОРКИ. ПОЛИГОН И ГИСТОГРАММА ЧАСТОТ
Статистическим распределением выборки называется соответствие между вариантами, то есть числовыми значениями признака, и их частотами или относительными частотами:
 |  |  | … |  |
 |  |  | … |  |
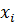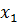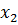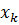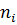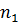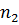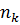Статистическое распределение бывает дискретным, то есть значения признака изолированы друг от друга, или непрерывным (интервальным) с непрерывно варьирующимся признаком.
Составление дискретного статистического распределения начинается с определения наименьшего и наибольшего значения, все остальные значения располагаются между ними в порядке возрастания.
Для непрерывно ‒ варьирующегося признака интервал его изменения разбивают на частичные интервалы одинаковой длины.
Для непрерывного распределения введем эмпирическую функцию распределения.
Эмпирической функцией распределения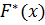 
или функцией распределения выборки называется функция, определяющая для каждого значения х относительную частоту события Х <х, то есть
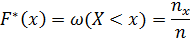
где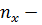 
число вариант, при которых наблюдаемое значение признака меньше х.
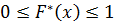
Наглядное представление о статистическом распределении дает график.
Для дискретного распределения по оси OX откладывают варианты, а по оси OY их частоты 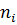. Полученные точки соединяют ломаной, которая вместе с осью ОХ образует полигон распределения частот.
Для непрерывного признака по оси OX откладывают частичные интервалы и строят на них прямоугольники с высотой 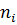. Полученная ступенчатая фигура называется гистограммой.
Если обвести гистограмму плавной линией, так чтобы примерно были равны площади, ограниченные ступенчатой ломаной и кривой, то получим график эмпирической функции распределения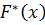 
.
Пример 1.Дискретное статистическое распределение.
В результате обследования 70 свиноматок по количеству поросят в одном помете составлено распределение:
| | |||||||||
| |
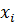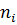Найти относительную частоту каждого значения признака и построить полигон распределения частот.
Решение:
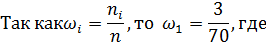
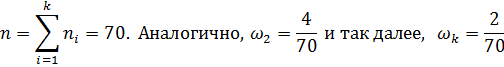
Найдем функцию распределения числа родившихся поросят:
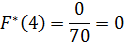
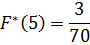
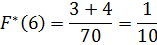
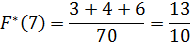
Полученные данные поместим в таблицу:
| | ||||||||||
| | ||||||||||
 |  |  |  |  |  |  |  |  |  |
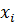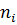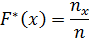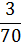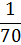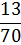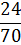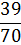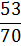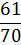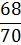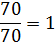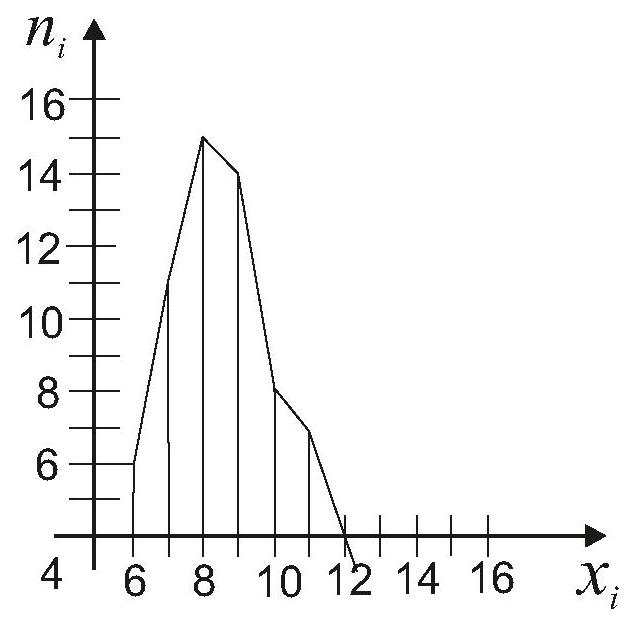
Пример 2.Непрерывное статистическое распределение.
При измерении длины 50 колосьев ячменя получены данные:
| Длина колоса, см. | 6…8 | 8…10 | 10…12 | 12…14 | 14…16 | 16…18 |
| |
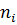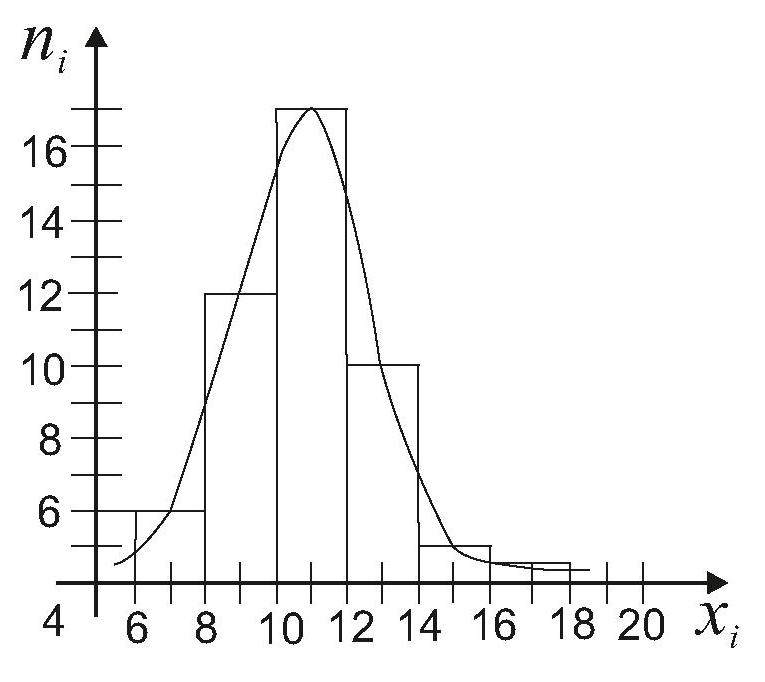
Построить гистограмму и эмпирическую функцию распределения выборки.
Решение:
Построим гистограмму:
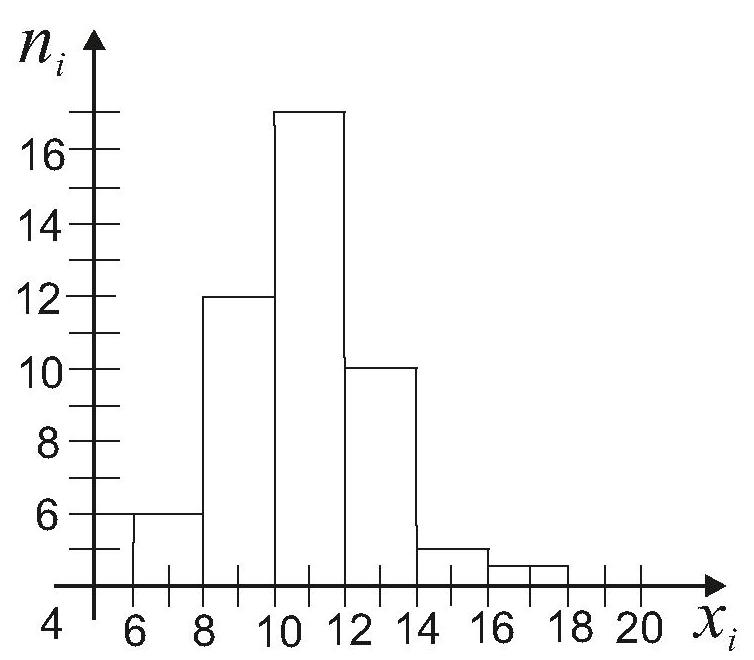
Построим эмпирическую функцию 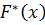распределения выборки:
