Коэффициент корреляции. Уравнение регрессии
Статистический анализ показателей поля месторождения
Расчеты для значения m:
1) Среднее значение Хср :
Хср =∑Хi/n=755,99/62=12,19
2) Cтандартное отклонение:
Ϭ=√∑Ϭ2/(n-1)=1,537
| m | Хср | Ϭi | Ϭ2 | Ϭ3 | Ϭ4 | |
| 1 | 14,75 | 12,1933871 | 2,56 | 6,536269537 | 16,71071 | 42,72282 |
| 2 | 13,82 | 1,63 | 2,645869537 | 4,303806 | 7,000626 | |
| 3 | 12,79 | 0,60 | 0,355946956 | 0,212363 | 0,126698 | |
| 4 | 11,85 | -0,34 | 0,117914698 | -0,04049 | 0,013904 | |
| 5 | 10,97 | -1,22 | 1,496675989 | -1,83101 | 2,240039 | |
| 6 | 9,91 | -2,28 | 5,213856634 | -11,9053 | 27,1843 | |
| 7 | 14,75 | 2,56 | 6,536269537 | 16,71071 | 42,72282 | |
| 8 | 13,69 | 1,50 | 2,239850182 | 3,352189 | 5,016929 | |
| 9 | 12,72 | 0,53 | 0,27732115 | 0,146041 | 0,076907 | |
| 10 | 11,64 | -0,55 | 0,306237279 | -0,16947 | 0,093781 | |
| 11 | 10,62 | -1,57 | 2,475546956 | -3,89499 | 6,128333 | |
| 12 | 14,59 | 2,40 | 5,743753408 | 13,76555 | 32,9907 | |
| 13 | 13,65 | 1,46 | 2,12172115 | 3,090526 | 4,501701 | |
| 14 | 12,67 | 0,48 | 0,22715986 | 0,108267 | 0,051602 | |
| 15 | 11,76 | -0,43 | 0,187824376 | -0,0814 | 0,035278 | |
| 16 | 10,84 | -1,35 | 1,831656634 | -2,47894 | 3,354966 | |
| 17 | 9,74 | -2,45 | 6,019108247 | -14,7672 | 36,22966 | |
| 18 | 14,14 | 1,95 | 3,789301795 | 7,376304 | 14,35881 | |
| 19 | 13,14 | 0,95 | 0,896075989 | 0,848237 | 0,802952 | |
| 20 | 12,22 | 0,03 | 0,000708247 | 1,88E-05 | 5,02E-07 | |
| 21 | 11,19 | -1,00 | 1,006785666 | -1,0102 | 1,013617 | |
| 22 | 10,14 | -2,05 | 4,216398569 | -8,6579 | 17,77802 | |
| 23 | 13,05 | 0,86 | 0,733785666 | 0,62857 | 0,538441 | |
| 24 | 12,14 | -0,05 | 0,002850182 | -0,00015 | 8,12E-06 | |
| 25 | 11,28 | -0,91 | 0,834275989 | -0,76202 | 0,696016 | |
| 26 | 10,36 | -1,83 | 3,361308247 | -6,16258 | 11,29839 | |
| 27 | 15,64 | 3,45 | 11,8791405 | 40,9428 | 141,114 | |
| 28 | 14,71 | 2,52 | 6,333340505 | 15,93857 | 40,1112 | |
| 29 | 13,62 | 1,43 | 2,035224376 | 2,903477 | 4,142138 | |
| 30 | 12,72 | 0,53 | 0,27732115 | 0,146041 | 0,076907 | |
| 31 | 11,68 | -0,51 | 0,263566311 | -0,13531 | 0,069467 | |
| 32 | 10,65 | -1,54 | 2,38204373 | -3,67642 | 5,674132 | |
| 33 | 15,08 | 2,89 | 8,332534053 | 24,0528 | 69,43112 | |
| 34 | 14,01 | 1,82 | 3,30008244 | 5,994972 | 10,89054 | |
| 35 | 13,02 | 0,83 | 0,683288892 | 0,564815 | 0,466884 | |
| 36 | 12,03 | -0,16 | 0,026695343 | -0,00436 | 0,000713 | |
| 37 | 11,20 | -0,99 | 0,986817924 | -0,98029 | 0,97381 | |
| 38 | 10,12 | -2,07 | 4,298934053 | -8,91335 | 18,48083 | |
| 39 | 12,13 | -0,06 | 0,004017924 | -0,00025 | 1,61E-05 | |
| 40 | 11,23 | -0,96 | 0,928114698 | -0,89413 | 0,861397 | |
| 41 | 10,26 | -1,93 | 3,737985666 | -7,22697 | 13,97254 | |
| 42 | 11,71 | -0,48 | 0,233663085 | -0,11295 | 0,054598 | |
| 43 | 10,86 | -1,33 | 1,77792115 | -2,37066 | 3,161004 | |
| 44 | 10,01 | -2,18 | 4,767179214 | -10,4086 | 22,726 | |
| 45 | 14,20 | 2,01 | 4,026495343 | 8,079618 | 16,21266 | |
| 46 | 13,21 | 1,02 | 1,033501795 | 1,050671 | 1,068126 | |
| 47 | 12,14 | -0,05 | 0,002850182 | -0,00015 | 8,12E-06 | |
| 48 | 11,17 | -1,02 | 1,04732115 | -1,07181 | 1,096882 | |
| 49 | 10,14 | -2,05 | 4,216398569 | -8,6579 | 17,77802 | |
| 50 | 13,11 | 0,92 | 0,840179214 | 0,770119 | 0,705901 | |
| 51 | 12,16 | -0,03 | 0,001114698 | -3,7E-05 | 1,24E-06 | |
| 52 | 11,07 | -1,12 | 1,261998569 | -1,41771 | 1,59264 | |
| 53 | 10,25 | -1,94 | 3,776753408 | -7,33969 | 14,26387 | |
| 54 | 14,30 | 2,11 | 4,437817924 | 9,348765 | 19,69423 | |
| 55 | 13,32 | 1,13 | 1,269256634 | 1,429961 | 1,611012 | |
| 56 | 12,21 | 0,02 | 0,000275989 | 4,58E-06 | 7,62E-08 | |
| 57 | 11,12 | -1,07 | 1,15215986 | -1,23671 | 1,327472 | |
| 58 | 10,10 | -2,09 | 4,382269537 | -9,17379 | 19,20429 | |
| 59 | 13,65 | 1,46 | 2,12172115 | 3,090526 | 4,501701 | |
| 60 | 12,57 | 0,38 | 0,141837279 | 0,053418 | 0,020118 | |
| 61 | 11,63 | -0,56 | 0,317405021 | -0,17882 | 0,100746 | |
| 62 | 10,54 | -1,65 | 2,733688892 | -4,51985 | 7,473055 | |
| ∑= | 755,99 | 0,00 | 144,1853887 | 61,53847 | 695,8353 |
3) Коэффициент вариации- мера рассеяния относительно среднего значения (%):
V= (Ϭ/Хср)*100%=12,61%
4) Интервал группирования показателя:
h=(xmax-xmin)/(1+3,22*lgN)=0,87
| N | класс | nk | Pk | Pk*100% |
| 9,74-10,61 | 0,177419 | 17,74194 | ||
| 10,62-11,49 | 0,193548 | 19,35484 | ||
| 11,50-12,37 | 0,209677 | 20,96774 | ||
| 12,38-13,25 | 0,16129 | 16,12903 | ||
| 13,26-14,13 | 0,112903 | 11,29032 | ||
| 14,14-15,01 | 0,112903 | 11,29032 | ||
| 15,02-15,89 | 0,032258 | 3,225806 | ||
| ∑ |
Гистограмма распределения значения m
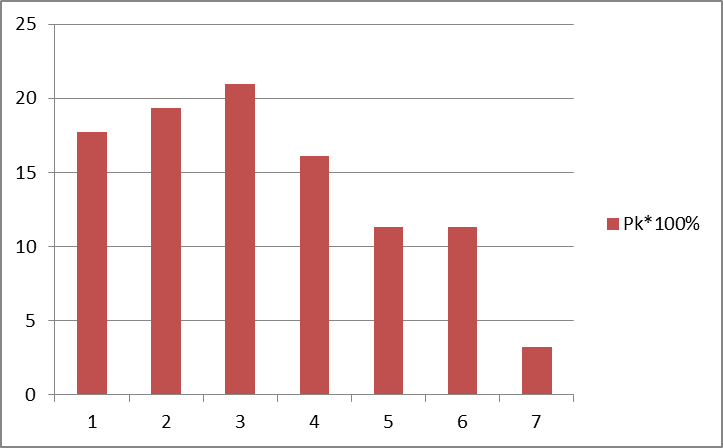
5) Мода- значение показателя с максимальной вероятностью:
Хmod= 14,75
6) Медиана- значение показателя, при котором гистограмма по площади делится пополам:
Хmed=12,14
7) Ассиметрия- мера сравнения с нормальным законом распределения, которая показывает меру скошенности исследуемой гистограммы относительно нормального закона распределения:
A=
8) Эксцесс показывает меру островершинности или туповершинности исследуемой гистограммы относительно нормального закона распределения:
Э=
Статистический анализ показателей поля месторождения
Расчеты для значения с:
1) Среднее значение Хср :
Хср =∑Хi/n= 923,58/62=14,89
2) Cтандартное отклонение:
Ϭ=√∑Ϭ2/(n-1)=1,24
| c | 14,89645 | Ϭi | Ϭ2 | Ϭ3 | Ϭ4 | |
| 1 | 17,00 | 2,10 | 4,42 | 9,31 | 19,58 | |
| 2 | 16,23 | 1,33 | 1,78 | 2,37 | 3,16 | |
| 3 | 15,38 | 0,48 | 0,23 | 0,11 | 0,05 | |
| 4 | 14,58 | -0,32 | 0,10 | -0,03 | 0,01 | |
| 5 | 13,93 | -0,97 | 0,93 | -0,90 | 0,87 | |
| 6 | 13,06 | -1,84 | 3,37 | -6,19 | 11,37 | |
| 7 | 16,92 | 2,02 | 4,09 | 8,29 | 16,77 | |
| 8 | 16,11 | 1,21 | 1,47 | 1,79 | 2,17 | |
| 9 | 15,32 | 0,42 | 0,18 | 0,08 | 0,03 | |
| 10 | 14,47 | -0,43 | 0,18 | -0,08 | 0,03 | |
| 11 | 13,61 | -1,29 | 1,65 | -2,13 | 2,74 | |
| 12 | 16,79 | 1,89 | 3,59 | 6,79 | 12,86 | |
| 13 | 16,04 | 1,14 | 1,31 | 1,50 | 1,71 | |
| 14 | 15,22 | 0,32 | 0,10 | 0,03 | 0,01 | |
| 15 | 14,48 | -0,42 | 0,17 | -0,07 | 0,03 | |
| 16 | 13,85 | -1,05 | 1,10 | -1,15 | 1,20 | |
| 17 | 12,91 | -1,99 | 3,95 | -7,84 | 15,57 | |
| 18 | 16,41 | 1,51 | 2,29 | 3,47 | 5,25 | |
| 19 | 15,61 | 0,71 | 0,51 | 0,36 | 0,26 | |
| 20 | 14,97 | 0,07 | 0,01 | 0,00 | 0,00 | |
| 21 | 14,03 | -0,87 | 0,75 | -0,65 | 0,56 | |
| 22 | 13,19 | -1,71 | 2,91 | -4,97 | 8,48 | |
| 23 | 15,61 | 0,71 | 0,51 | 0,36 | 0,26 | |
| 24 | 14,81 | -0,09 | 0,01 | 0,00 | 0,00 | |
| 25 | 14,10 | -0,80 | 0,63 | -0,51 | 0,40 | |
| 26 | 13,47 | -1,43 | 2,03 | -2,90 | 4,14 | |
| 27 | 17,68 | 2,78 | 7,75 | 21,57 | 60,03 | |
| 28 | 16,85 | 1,95 | 3,82 | 7,46 | 14,56 | |
| 29 | 16,01 | 1,11 | 1,24 | 1,38 | 1,54 | |
| 30 | 15,35 | 0,45 | 0,21 | 0,09 | 0,04 | |
| 31 | 14,55 | -0,35 | 0,12 | -0,04 | 0,01 | |
| 32 | 13,67 | -1,23 | 1,50 | -1,84 | 2,26 | |
| 33 | 17,21 | 2,31 | 5,35 | 12,38 | 28,65 | |
| 34 | 16,29 | 1,39 | 1,94 | 2,71 | 3,77 | |
| 35 | 15,58 | 0,68 | 0,47 | 0,32 | 0,22 | |
| 36 | 14,80 | -0,10 | 0,01 | 0,00 | 0,00 | |
| 37 | 14,12 | -0,78 | 0,60 | -0,47 | 0,36 | |
| 38 | 13,15 | -1,75 | 3,05 | -5,33 | 9,30 | |
| 39 | 14,87 | -0,03 | 0,00 | 0,00 | 0,00 | |
| 40 | 14,16 | -0,74 | 0,54 | -0,40 | 0,29 | |
| 41 | 13,34 | -1,56 | 2,42 | -3,77 | 5,87 | |
| 42 | 14,52 | -0,38 | 0,14 | -0,05 | 0,02 | |
| 43 | 13,86 | -1,04 | 1,07 | -1,11 | 1,15 | |
| 44 | 13,11 | -1,79 | 3,19 | -5,70 | 10,19 | |
| 45 | 16,60 | 1,70 | 2,90 | 4,94 | 8,42 | |
| 46 | 15,81 | 0,91 | 0,83 | 0,76 | 0,70 | |
| 47 | 14,84 | -0,06 | 0,00 | 0,00 | 0,00 | |
| 48 | 14,14 | -0,76 | 0,57 | -0,43 | 0,33 | |
| 49 | 13,21 | -1,69 | 2,84 | -4,80 | 8,09 | |
| 50 | 15,67 | 0,77 | 0,60 | 0,46 | 0,36 | |
| 51 | 14,84 | -0,06 | 0,00 | 0,00 | 0,00 | |
| 52 | 13,95 | -0,95 | 0,90 | -0,85 | 0,80 | |
| 53 | 13,32 | -1,58 | 2,49 | -3,92 | 6,18 | |
| 54 | 16,59 | 1,69 | 2,87 | 4,86 | 8,23 | |
| 55 | 15,90 | 1,00 | 1,01 | 1,01 | 1,01 | |
| 56 | 14,85 | -0,05 | 0,00 | 0,00 | 0,00 | |
| 57 | 14,06 | -0,84 | 0,70 | -0,59 | 0,49 | |
| 58 | 13,24 | -1,66 | 2,74 | -4,55 | 7,53 | |
| 59 | 16,07 | 1,17 | 1,38 | 1,62 | 1,90 | |
| 60 | 15,15 | 0,25 | 0,06 | 0,02 | 0,00 | |
| 61 | 14,50 | -0,40 | 0,16 | -0,06 | 0,02 | |
| 62 | 13,62 | -1,28 | 1,63 | -2,08 | 2,65 | |
| ∑ | 923,58 | 0,00 | 93,41 | 30,62 | 292,52 |
3) Коэффициент вариации- мера рассеяния относительно среднего значения (%):
V= (Ϭ/Хср)*100%=8,3%
4) Интервал группирования показателя:
h=(xmax-xmin)/(1+3,22*lgN)=0,7
| N | класс | nk | Pk | Pk*100% |
| 12,91-13,61 | 0,177419 | 17,74194 | ||
| 13,62-14,32 | 0,193548 | 19,35484 | ||
| 14,33-15,03 | 0,209677 | 20,96774 | ||
| 15,04-15,74 | 0,145161 | 14,51613 | ||
| 15,75-16,45 | 0,145161 | 14,51613 | ||
| 16,46-17,16 | 0,096774 | 9,677419 | ||
| 17,17-17,87 | 0,032258 | 3,225806 | ||
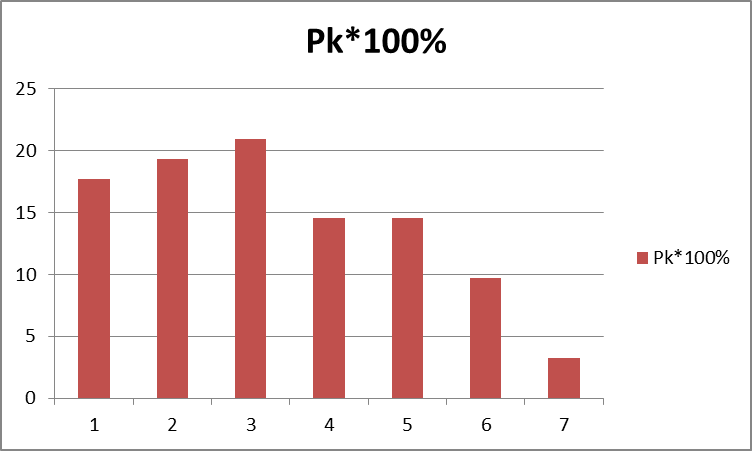
5) Мода- значение показателя с максимальной вероятностью:
Хmod= 15,61
6) Медиана- значение показателя, при котором гистограмма по площади делится пополам:
Хmed=14,83
7) Ассиметрия- мера сравнения с нормальным законом распределения, которая показывает меру скошенности исследуемой гистограммы относительно нормального закона распределения:
A=
8) Эксцесс показывает меру островершинности или туповершинности исследуемой гистограммы относительно нормального закона распределения:
Э=
Вывод: Собранные нами данные (содержание п.и.), выбранного поля месторождения, служат источниками информации в процессе анализа с использованием различных статистических методов и выработке мер по улучшению. Максимальное значение частоты распределения зафиксировано в интервале 11,50-12,37, Р=20,9%
Собранные нами данные ( п.и.), выбранного поля месторождения, служат источниками информации в процессе анализа с использованием различных статистических методов и выработке мер по улучшению. Максимальное значение частоты распределения зафиксировано в интервале
Коэффициент корреляции. Уравнение регрессии.
Между показателями месторождения обычно существуют некоторые связи, которые могут быть описаны математическими формулами.
Если связь между двумя показателями m,c линейная, то мера связи определяется с помощью коэффициента корреляции rxy.
rxy- пример линейной связи, которая измеряется от -1 до +1
Если эта мера или rxy =0, то между показателями линейная связь отсутствует.
Если rxy =-1(+1), то связь между показателями линейная и детерминированная (закономерная). Причем, если rxy=+1, то связь прямая, если rxy=-1, то обратная.
Если rxy˂1, то связь между показателями случайная и линейная.
rxy=Σδxiδyi/nδxδy, где δxi=xi-x; δyi=yi-y.
Коэффициент детерминации D=r2xy
Считается, что мера линейной связи между показателями устойчива, если D˃0.5 =˃ rxy˃0.71
Уравнение регрессии- линейное уравнение связи между двумя показателями –прогнозное уравнение.
Yi=α+βxi; Сi=α+βmi.
Основной задачей уравнения регрессии является определение постоянных коэффициентов β и α.
Коэффициент корреляции. Уравнение регрессии
| n | xi | yi | xi^2 | yi^2 | Xiyi | ỹi | ỹi-yi | (ỹi-yi)^2 |
| 1 | 14,75 | 17,00 | 217,56 | 289,00 | 250,75 | 16,95293 | -0,05 | 0,002 |
| 2 | 13,82 | 16,23 | 190,99 | 263,41 | 224,2986 | 16,20486 | -0,03 | 0,001 |
| 3 | 12,79 | 15,38 | 163,58 | 236,54 | 196,7102 | 15,37635 | 0,00 | 0,000 |
| 4 | 11,85 | 14,58 | 140,42 | 212,58 | 172,773 | 14,62024 | 0,04 | 0,002 |
| 5 | 10,97 | 13,93 | 120,34 | 194,04 | 152,8121 | 13,91239 | -0,02 | 0,000 |
| 6 | 9,91 | 13,06 | 98,21 | 170,56 | 129,4246 | 13,05975 | 0,00 | 0,000 |
| 7 | 14,75 | 16,92 | 217,56 | 286,29 | 249,57 | 16,95293 | 0,03 | 0,001 |
| 8 | 13,69 | 16,11 | 187,42 | 259,53 | 220,5459 | 16,10029 | -0,01 | 0,000 |
| 9 | 12,72 | 15,32 | 161,80 | 234,70 | 194,8704 | 15,32005 | 0,00 | 0,000 |
| 10 | 11,64 | 14,47 | 135,49 | 209,38 | 168,4308 | 14,45132 | -0,02 | 0,000 |
| 11 | 10,62 | 13,61 | 112,78 | 185,23 | 144,5382 | 13,63085 | 0,02 | 0,000 |
| 12 | 14,59 | 16,79 | 212,87 | 281,90 | 244,9661 | 16,82423 | 0,03 | 0,001 |
| 13 | 13,65 | 16,04 | 186,32 | 257,28 | 218,946 | 16,06812 | 0,03 | 0,001 |
| 14 | 12,67 | 15,22 | 160,53 | 231,65 | 192,8374 | 15,27983 | 0,06 | 0,004 |
| 15 | 11,76 | 14,48 | 138,30 | 209,67 | 170,2848 | 14,54784 | 0,07 | 0,005 |
| 16 | 10,84 | 13,85 | 117,51 | 191,82 | 150,134 | 13,80782 | -0,04 | 0,002 |
| 17 | 9,74 | 12,91 | 94,87 | 166,67 | 125,7434 | 12,923 | 0,01 | 0,000 |
| 18 | 14,14 | 16,41 | 199,94 | 269,29 | 232,0374 | 16,46226 | 0,05 | 0,003 |
| 19 | 13,14 | 15,61 | 172,66 | 243,67 | 205,1154 | 15,65789 | 0,05 | 0,002 |
| 20 | 12,22 | 14,97 | 149,33 | 224,10 | 182,9334 | 14,91786 | -0,05 | 0,003 |
| 21 | 11,19 | 14,03 | 125,22 | 196,84 | 156,9957 | 14,08935 | 0,06 | 0,004 |
| 22 | 10,14 | 13,19 | 102,82 | 173,98 | 133,7466 | 13,24475 | 0,05 | 0,003 |
| 23 | 13,05 | 15,61 | 170,30 | 243,67 | 203,7105 | 15,58549 | -0,02 | 0,001 |
| 24 | 12,14 | 14,81 | 147,38 | 219,34 | 179,7934 | 14,85351 | 0,04 | 0,002 |
| 25 | 11,28 | 14,10 | 127,24 | 198,81 | 159,048 | 14,16174 | 0,06 | 0,004 |
| 26 | 10,36 | 13,47 | 107,33 | 181,44 | 139,5492 | 13,42172 | -0,05 | 0,002 |
| 27 | 15,64 | 17,68 | 244,61 | 312,58 | 276,5152 | 17,66883 | -0,01 | 0,000 |
| 28 | 14,71 | 16,85 | 216,38 | 283,92 | 247,8635 | 16,92076 | 0,07 | 0,005 |
| 29 | 13,62 | 16,01 | 185,50 | 256,32 | 218,0562 | 16,04399 | 0,03 | 0,001 |
| 30 | 12,72 | 15,35 | 161,80 | 235,62 | 195,252 | 15,32005 | -0,03 | 0,001 |
| 31 | 11,68 | 14,55 | 136,42 | 211,70 | 169,944 | 14,48349 | -0,07 | 0,004 |
| 32 | 10,65 | 13,67 | 113,42 | 186,87 | 145,5855 | 13,65499 | -0,02 | 0,000 |
| 33 | 15,08 | 17,21 | 227,41 | 296,18 | 259,5268 | 17,21838 | 0,01 | 0,000 |
| 34 | 14,01 | 16,29 | 196,28 | 265,36 | 228,2229 | 16,35769 | 0,07 | 0,005 |
| 35 | 13,02 | 15,58 | 169,52 | 242,74 | 202,8516 | 15,56136 | -0,02 | 0,000 |
| 36 | 12,03 | 14,80 | 144,72 | 219,04 | 178,044 | 14,76503 | -0,03 | 0,001 |
| 37 | 11,20 | 14,12 | 125,44 | 199,37 | 158,144 | 14,09739 | -0,02 | 0,001 |
| 38 | 10,12 | 13,15 | 102,41 | 172,92 | 133,078 | 13,22866 | 0,08 | 0,006 |
| 39 | 12,13 | 14,87 | 147,14 | 221,12 | 180,3731 | 14,84546 | -0,02 | 0,001 |
| 40 | 11,23 | 14,16 | 126,11 | 200,51 | 159,0168 | 14,12152 | -0,04 | 0,001 |
| 41 | 10,26 | 13,34 | 105,27 | 177,96 | 136,8684 | 13,34128 | 0,00 | 0,000 |
| 42 | 11,71 | 14,52 | 137,12 | 210,83 | 170,0292 | 14,50763 | -0,01 | 0,000 |
| 43 | 10,86 | 13,86 | 117,94 | 192,10 | 150,5196 | 13,8239 | -0,04 | 0,001 |
| 44 | 10,01 | 13,11 | 100,20 | 171,87 | 131,2311 | 13,14018 | 0,03 | 0,001 |
| 45 | 14,20 | 16,60 | 201,64 | 275,56 | 235,72 | 16,51053 | -0,09 | 0,008 |
| 46 | 13,21 | 15,81 | 174,50 | 249,96 | 208,8501 | 15,71419 | -0,10 | 0,009 |
| 47 | 12,14 | 14,84 | 147,38 | 220,23 | 180,1576 | 14,85351 | 0,01 | 0,000 |
| 48 | 11,17 | 14,14 | 124,77 | 199,94 | 157,9438 | 14,07326 | -0,07 | 0,004 |
| 49 | 10,14 | 13,21 | 102,82 | 174,50 | 133,9494 | 13,24475 | 0,03 | 0,001 |
| 50 | 13,11 | 15,67 | 171,87 | 245,55 | 205,4337 | 15,63375 | -0,04 | 0,001 |
| 51 | 12,16 | 14,84 | 147,87 | 220,23 | 180,4544 | 14,8696 | 0,03 | 0,001 |
| 52 | 11,07 | 13,95 | 122,54 | 194,60 | 154,4265 | 13,99282 | 0,04 | 0,002 |
| 53 | 10,25 | 13,32 | 105,06 | 177,42 | 136,53 | 13,33323 | 0,01 | 0,000 |
| 54 | 14,30 | 16,59 | 204,49 | 275,23 | 237,237 | 16,59096 | 0,00 | 0,000 |
| 55 | 13,32 | 15,90 | 177,42 | 252,81 | 211,788 | 15,80267 | -0,10 | 0,009 |
| 56 | 12,21 | 14,85 | 149,08 | 220,52 | 181,3185 | 14,90981 | 0,06 | 0,004 |
| 57 | 11,12 | 14,06 | 123,65 | 197,68 | 156,3472 | 14,03304 | -0,03 | 0,001 |
| 58 | 10,10 | 13,24 | 102,01 | 175,30 | 133,724 | 13,21258 | -0,03 | 0,001 |
| 59 | 13,65 | 16,07 | 186,32 | 258,24 | 219,3555 | 16,06812 | 0,00 | 0,000 |
| 60 | 12,57 | 15,15 | 158,00 | 229,52 | 190,4355 | 15,19939 | 0,05 | 0,002 |
| 61 | 11,63 | 14,50 | 135,26 | 210,25 | 168,635 | 14,44328 | -0,06 | 0,003 |
| 62 | 10,54 | 13,62 | 111,09 | 185,50 | 143,5548 | 13,5665 | -0,05 | 0,003 |
| 62 | ||||||||
| ∑ | 755,99 | 923,58 | 9362,26 | 13851,48 | 11377,55 | 923,58 | 0,00 | 0,12 |
| ср | 12,19339 | 14,89645 | 151,0043 | 223,4109 | 183,5088 | 14,89645 | 0,001955361 | |
| β | 0,804378 | Wv(xy) | 1,870638 | |||||
| α | 5,08836 | Rxy | ||||||
| xср | 12,19339 | Ϭ²x | ||||||
| yср | 14,89645 | Ϭ²y | ||||||
| Mxx | 151,0043 | Ϭx | ||||||
| Mxy | 183,5088 | Ϭy |
Уравнение регрессии Y=5,08+0,8*хi
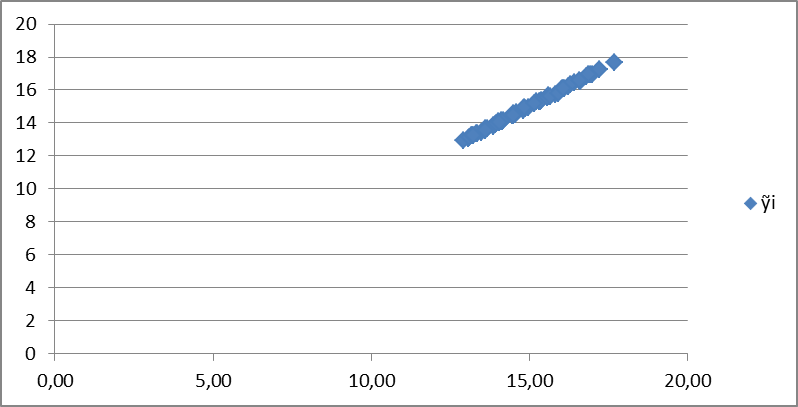
Вывод: при помощи этой части мы можем видеть отклонения каждой точки от линии регрессии. Для лучшей интерпретации этих данных строят график исходных данных и построенной линией регрессии.
Автокорреляция. Определение радиуса автокорреляции
| хi | Ϭ | m=1 | m=2 | m=3 | Ϭ² | |
| 1 | 14,75 | 2,75 | 7,56 | |||
| 2 | 13,82 | 1,82 | 5,005725 | 3,31 | ||
| 3 | 12,79 | 0,79 | 1,438214 | 2,173062 | 0,62 | |
| 4 | 11,85 | -0,15 | -0,1184 | -0,27273 | -0,41209 | 0,02 |
| 5 | 10,97 | -1,03 | 0,154313 | -0,81374 | -1,87447 | 1,06 |
| 6 | 9,91 | -2,09 | 2,152205 | 0,313144 | -1,65131 | 4,37 |
| 7 | 14,75 | 2,75 | -5,7474 | -2,83223 | -0,41209 | 7,56 |
| 8 | 13,69 | 1,69 | 4,648205 | -3,53216 | -1,7406 | 2,86 |
| 9 | 12,72 | 0,72 | 1,217183 | 1,980551 | -1,50502 | 0,52 |
| 10 | 11,64 | -0,36 | -0,25914 | -0,60819 | -0,98962 | 0,13 |
| 11 | 10,62 | -1,38 | 0,496524 | -0,9937 | -2,33215 | 1,90 |
| 12 | 14,59 | 2,59 | -3,57401 | -0,93205 | 1,865325 | 6,71 |
| 13 | 13,65 | 1,65 | 4,274173 | -2,27696 | -0,5938 | 2,72 |
| 14 | 12,67 | 0,67 | 1,105868 | 1,735817 | -0,92471 | 0,45 |
| 15 | 11,76 | -0,24 | -0,16073 | -0,39578 | -0,62123 | 0,06 |
| 16 | 10,84 | -1,16 | 0,278178 | -0,77728 | -1,91392 | 1,35 |
| 17 | 9,74 | -2,26 | 2,621057 | 0,542003 | -1,51445 | 5,11 |
| 18 | 14,14 | 2,14 | -4,83642 | -2,48224 | -0,5133 | 4,58 |
| 19 | 13,14 | 1,14 | 2,440121 | -2,57658 | -1,3224 | 1,30 |
| 20 | 12,22 | 0,22 | 0,251016 | 0,471175 | -0,49752 | 0,05 |
| 21 | 11,19 | -0,81 | -0,17829 | -0,92335 | -1,73319 | 0,66 |
| 22 | 10,14 | -1,86 | 1,506176 | -0,40946 | -2,12051 | 3,46 |
| 23 | 13,05 | 1,05 | -1,95313 | -0,85046 | 0,231202 | 1,10 |
| 24 | 12,14 | 0,14 | 0,147189 | -0,26067 | -0,11351 | 0,02 |
| 25 | 11,28 | -0,72 | -0,10089 | -0,75595 | 1,338791 | 0,52 |
| 26 | 10,36 | -1,64 | 1,180425 | -0,22984 | -1,72209 | 2,69 |
| 27 | 15,64 | 3,64 | -5,96928 | -2,62034 | 0,5102 | 13,25 |
| 28 | 14,71 | 2,71 | 9,865408 | -4,44423 | -1,95088 | 7,34 |
| 29 | 13,62 | 1,62 | 4,390887 | 5,897635 | -2,6568 | 2,62 |
| 30 | 12,72 | 0,72 | 1,166771 | 1,951744 | 2,621492 | 0,52 |
| 31 | 11,68 | -0,32 | -0,23034 | -0,51819 | -0,86682 | 0,10 |
| 32 | 10,65 | -1,35 | 0,431735 | -0,9721 | -2,18696 | 1,82 |
| 33 | 15,08 | 3,08 | -4,15773 | -0,98516 | 2,218203 | 9,49 |
| 34 | 14,01 | 2,01 | 6,191608 | -2,7134 | -0,64293 | 4,04 |
| 35 | 13,02 | 1,02 | 2,050681 | 3,142251 | -1,37705 | 1,04 |
| 36 | 12,03 | 0,03 | 0,030767 | 0,060624 | 0,092894 | 0,00 |
| 37 | 11,20 | -0,80 | -0,02412 | -0,81597 | -1,60781 | 0,64 |
| 38 | 10,12 | -1,88 | 1,503575 | -0,05669 | -1,91774 | 3,53 |
| 39 | 12,13 | 0,13 | -0,24468 | -0,10411 | 0,003925 | 0,02 |
| 40 | 11,23 | -0,77 | -0,1002 | 1,447179 | 0,615751 | 0,59 |
| 41 | 10,26 | -1,74 | 1,339402 | -0,22646 | 3,270625 | 3,03 |
| 42 | 11,71 | -0,29 | 0,504278 | 0,223132 | -0,03773 | 0,08 |
| 43 | 10,86 | -1,14 | 0,330373 | 1,983143 | 0,877497 | 1,30 |
| 44 | 10,01 | -1,99 | 2,268103 | 0,576738 | 3,462008 | 3,96 |
| 45 | 14,20 | 2,20 | -4,37797 | -2,50783 | -0,6377 | 4,84 |
| 46 | 13,21 | 1,21 | 2,662541 | -2,40802 | -1,37939 | 1,46 |
| 47 | 12,14 | 0,14 | 0,169614 | 0,308371 | -0,27889 | 0,02 |
| 48 | 11,17 | -0,83 | -0,11631 | -1,00424 | -1,82578 | 0,69 |
| 49 | 10,14 | -1,86 | 1,543373 | -0,26067 | -2,2507 | 3,46 |
| 50 | 13,11 | 1,11 | -2,06472 | -0,92126 | 0,155598 | 1,23 |
| 51 | 12,16 | 0,16 | 0,177802 | -0,29787 | -0,13291 | 0,03 |
| 52 | 11,07 | -0,93 | -0,14892 | -1,03227 | 1,729357 | 0,86 |
| 53 | 10,25 | -1,75 | 1,627075 | -0,28025 | -1,9426 | 3,06 |
| 54 | 14,30 | 2,30 | -4,02491 | -2,13878 | 0,368391 | 5,29 |
| 55 | 13,32 | 1,32 | 3,036575 | -2,31007 | -1,22754 | 1,74 |
| 56 | 12,21 | 0,21 | 0,277443 | 0,483398 | -0,36774 | 0,04 |
| 57 | 11,12 | -0,88 | -0,18491 | -1,16153 | -2,02377 | 0,77 |
| 58 | 10,10 | -1,90 | 1,671559 | -0,39927 | -2,50809 | 3,61 |
| 59 | 13,65 | 1,65 | -3,13504 | -1,45188 | 0,346795 | 2,72 |
| 60 | 12,57 | 0,57 | 0,940852 | -1,08321 | -0,50165 | 0,33 |
| 61 | 11,63 | -0,37 | -0,21087 | -0,6103 | 0,70264 | 0,14 |
| 62 | 10,54 | -1,46 | 0,53991 | -0,83234 | -2,40897 | 2,13 |
| сумма | 755,99 | 12,00 | 29,7185 | -30,7898 | -34,8277 | 146,51 |
| cр | 11,99984 |
r(1)=0,003
r(2)=-0,003
r(3)=-0,004
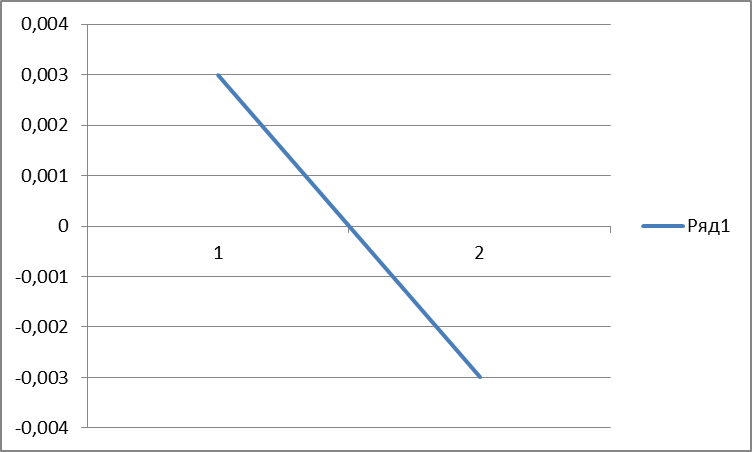
Вывод: по результатам вычислений был построен график и графически определен радиус автокорреляции который равен 1,5 м.
Автокорреляция. Определение радиуса автокорреляции
