Линейных математических моделей

В качестве примера рассмотрим реальную схему электрической системы (рис.2.1), которая включает в себя тепловую электростанцию (ТЭС), линии электропередач различных номинальных напряжений (Л1-Л6), понизительные подстанции и обобщенные нагрузки (Н1-Н4).

Рис. 2.1

Предварительным этапом перед проведением расчета установившегося режима является переход от принципиальной к схеме замещения, а затем к расчетной схеме, формируемой на основе теории графов.

Под схемой замещения ЭС понимается совокупность схем замещения отдельных элементов, соединенных в той же последовательности, что и в реальной схеме.

Теория формирования схем замещения рассматривается в специальных курсах. Ограничимся примером формирования схемы замещения простейшей электрической системы, в объеме необходимом для понимания структуры расчетной схемы.

Будем рассматривать симметричные установившиеся режимы, при которых используется схема замещения одной фазы.

Принципиальная схема любой ЭС включает в себя три группы элементов:

· источники энергии,

· потребители или нагрузку

· электрические сети, соединяющие источники с потребителями.

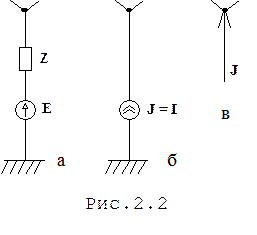Возможны следующие варианты схем замещения для источников энергии: источник напряжения с ЭДС и внутренним сопротивлением 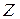(рис.2.2,а); источник тока J, равный току установившегося режима (рис.2.2,б); задающий ток J, равный току источника тока (рис.2.2,в). Использование задающих токов J, как модели источника энергии, повышает наглядность схем замещения сложных электрических систем.

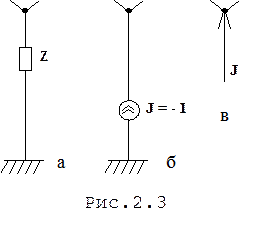
Потребители электроэнергии (нагрузка) моделируются с помощью следующих схем замещения : сопротивление нагрузки Z (рис.2.3,а); источник тока J, равный взятому с обратным знаком току нагрузки (рис.2.3,б); задающий ток J, равный току источника тока (рис.2.3,в);

Схемы замещения элементов электрической сети представляют собой сопротивления Z , причем схемы замещения трансформаторов подстанций объединяются со схемами замещения источников энергии и нагрузок.

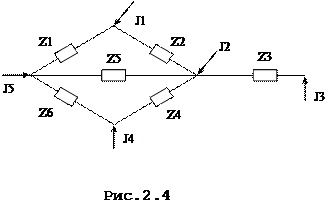
С учетом рассмотренных схем замещения отдельных элементов, приведем вариант схемы замещения (рис.2.4) электрической системы, представленной на рис.2.1.

При этом произведем, известные из курса ТОЭ, преобразования: приведем схемы к одному номинальному напряжению, схемы замещения трансформаторов подстанций объединим со схемами замещения источников питания и нагрузок; смоделируем нагрузку и генерацию мощности с помощью задающих токов.

Введены обозначения полученных в ходе преобразования сопротивлений и узлов схемы замещения, из которых один узел генераторный и 4 узла — нагрузочных.

По такой схеме замещения может быть составлен топографический направленный граф, который используется как расчетная схема (рис.2.5).

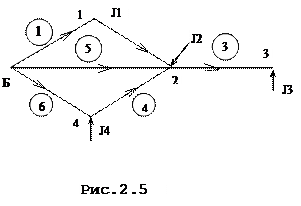
Данная расчетная схема содержит четыре независимых узла (1, 2, 3, 4) и один балансирующий узел (Б). Задающие токи в узлах 1,2,3,4 моделируют нагрузку и имеют отрицательные значения. В качестве балансирующего выбран генераторный узел, в котором задано значение напряжения 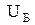. Каждая ветвь схемы имеет произвольное направление.

Расчетная схема содержит два независимых контура (I, II), направление обхода каждого заданно произвольно.

Схемы замещения современных электрических систем имеют сотни узлов и ветвей, образующих сложно-замкнутую структуру. Расчет режимов функционирования подобных технических систем невозможен без использования вычислительной техники. Поэтому важное значение приобретает использование единого формализованного подхода, основанного на аппарате алгебры матриц и позволяющего дать описание схем любой сложности и конфигурации. Матричная форма представления обеспечивает компактность и наглядность представления большого количества исходной и результирующей информации при проведении расчета режимов сложных схем.