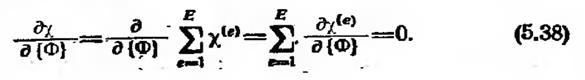Уравнения метода конечных элементов: задачи теории поля

Одномерная задача распространения тепла, рассмотренная в предыдущих разделах, является одной из нескольких важных физических задач, которые могут быть описаны аналогичными дифференциальными уравнениями в частных производных. Дифференциальное уравнение для каждого из этих физических процессов содержится в общем квазигармоническом уравнении

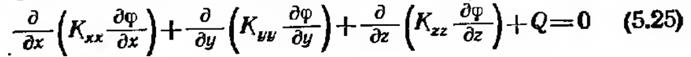с граничными условиями

и (или)

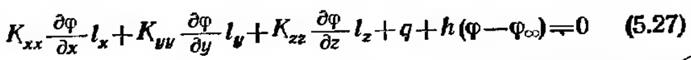на S2. Объединение Si и S2 образует полную границу. Коэффициенты Кхх, Куу и Kzz, а также величина q могут быть функциями х, у и г, но предполагаются независимыми от ф. Величины 1Х, 1У и /г в формуле (5.27) — направляющие косинусы вектора нормали к поверхности. Уравнение (5.25) применимо как к изотропным, так и к анизотропным телам. Координатные оси, однако, должны быть параллельны главным осям инерции в анизотропных областях.

Уравнение (5.25) вместе с граничными условиями описывает распространение тепла в трехмерной области [4]. В этом случае Кхх, Куу и Kzz соответствуют коэффициентам теплопроводности, Q — внутренний источник тепла или сток, q — тепловой поток на части поверхности и h — коэффициент теплообмена. Полевая функция ф определяет температуру тела. Уравнение для одномерного и двумерного случаев распространения тепла может быть получено из формулы (5.25) с учетом того, что сйр/ду 0 и (или) дц>/дг = 0. Если на той части границы, где ф не определено (на Sг), обе величины q и h равны нулю, равенство (5.27) сводится к следующему условию:

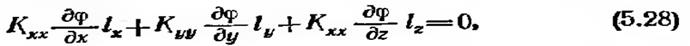которое отражает отсутствие переноса тепла (теплоизолированная граница).

Рассмотрим далее двумерную ситуацию, когда Кхх~ Куу — 1, Q = 2G0 и фв = 0 на всей границе. В этом случае уравнение (5.25) сводится к следующему уравнению:

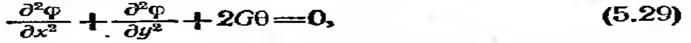которое встречается в задаче о кручении упругого стержня не- кругового сечения [5]. Полевая функция ф теперь является функцией напряжений, G — упругая характеристика материала, 0 —угол закручивания сечения стержня. Напряжения сдвига, вызванные внешним крутящим усилием, получаются дифференцированием ф по х и у.

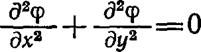Другой важной двумерной задачей является задача о безвихревом течении жидкости. В этом примере Кхх = КУу = 1, Q=0 и уравнение (5.25) сводится к уравнению

с граничными условиями ф = фв и (ду/дх)1х+ (ду/ду)1у = 0 [6]. Если полевая функция ф задана на непроницаемых границах области (на границах, по нормали к которым не происходит течения жидкости), то уравнение (5 30) определяет линии тока при безвихревом течении жидкости. С другой стороны, если полевая функция определена на тех частях границы, по нормали к которым течет жидкость, то уравнение (5.30) описывает эквипотенциальные линии, которые ортогональны линиям тока.

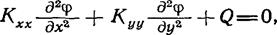Дифференциальное уравнение для ограниченного потока грунтовых вод [2] также содержится в (5.25). В этом случае

(5.31)

а граничные условия имеют вид ф = фв и (или) Kxx(d(p!dx)tx+ -\-Куу {dqjdy) ly-\-q = 0. Коэффициенты Кхх и Куу определяют проницаемость почвы, Q — источник (или сток) воды, а полевая функция ф — пьезометрический напор. Величина q соответствует просачиванию воды через водоносный слой вдоль части его границы.

Другие важные физические задачи, которые описываются уравнением (5.25), связаны с рассмотрением электростатического и магнитостатического полей, а также жидких смазочных пленок. Последняя задача подробно изучена в работе [3].

С вариационной точки зрения решение уравнения (5.25) с граничными условиями (5.26) и (5.27) эквивалентно отысканию минимума функционала

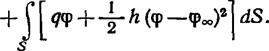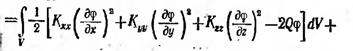* (5.32)

Минимизация функционала (5.32) должна быть осуществлена на множестве узловых значений {Ф}. Для этой цели воспользуемся процедурой, рассмотренной в предыдущем разделе, а именно будем минимизировать функционал (5.32) перед вычислением интегралов.

Этот подход позволяет выбрать характеристики элементов, наиболее приемлемые для каждой конкретной задачи.

Начнем процесс минимизации с преобразования функционала

. Этот шаг несколько упрощает последующие операции. Введем две матрицы: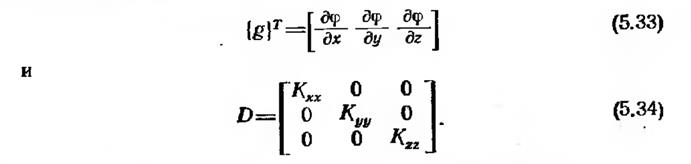

Соотношение (5.32) может быть теперь записано в виде

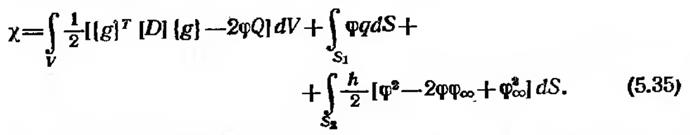Вспоминая, что функции от <р не являются непрерывными во всей области, вместо них введем в рассмотрение функции <р(е>, определенные на отдельных элементах. Интегралы в (5.35) должны быть разбиты на интегралы по отдельным элементам, что дает ё

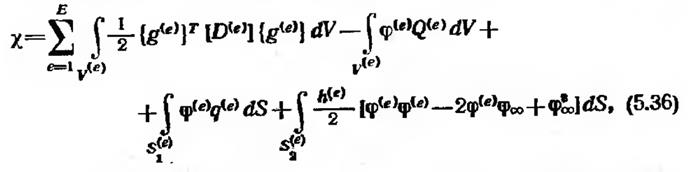где Е — общее число элементов. Последнее соотношение может быть символически записано как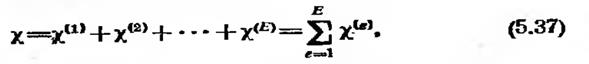

где —вклад отдельного элемента в Минимизация x требует выполнения соотношения