Постановка задачи. Различные формулировки
Рассмотрим на промежутке (0, 1) краевую задачу
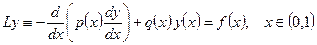 ; (1.4)
; (1.4)
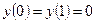 (1.5)
(1.5)
при следующих предположениях:
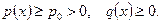
Эта краевая задача служит математической моделью многих физических процессов, так, например, она описывает распределение температуры в неоднородном стержне или концентрацию вещества при диффузии.
Охарактеризуем исходные данные этой краевой задачи. Будем считать, что правая часть 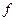 принадлежит пространству
принадлежит пространству 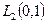 . Такой класс правых частей достаточно широк и обслуживает широкий круг практических задач. Напомним, что
. Такой класс правых частей достаточно широк и обслуживает широкий круг практических задач. Напомним, что 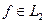 , если конечна норма
, если конечна норма
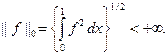
Пусть 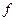 и
и 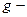 функции из
функции из 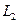 . Их скалярным произведением называют число
. Их скалярным произведением называют число
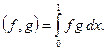
Заметим, что 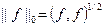 . Пространству
. Пространству 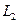 принадлежат, например, кусочно-непрерывные, ограниченные функции.
принадлежат, например, кусочно-непрерывные, ограниченные функции.
Если функция 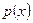 имеет ограниченную производную, а функция
имеет ограниченную производную, а функция 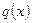 ограничена, то краевая задача, которую мы рассматриваем, имеет единственное решение и оно принадлежит пространству
ограничена, то краевая задача, которую мы рассматриваем, имеет единственное решение и оно принадлежит пространству 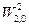 функций, имеющих производные второго порядка. Норма функций в этом пространстве определяется так:
функций, имеющих производные второго порядка. Норма функций в этом пространстве определяется так:
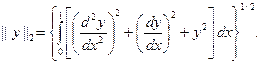
Значок ''нолик'' в обозначении пространства 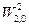 указывает, что функции, входящие в это пространство, удовлетворяют краевым условиям (1.5). Пространству
указывает, что функции, входящие в это пространство, удовлетворяют краевым условиям (1.5). Пространству 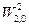 , например, принадлежат функции, имеющие ограниченную вторую производную.
, например, принадлежат функции, имеющие ограниченную вторую производную.
Введем в рассмотрение еще одно пространство – пространство функций, имеющих ограниченную норму
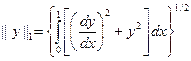
и удовлетворяющих краевым условиям (1.5). Обозначим его 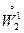 . Этому пространству принадлежат, например, непрерывные функции, имеющие ограниченную производную. Заметим, что любая функция из
. Этому пространству принадлежат, например, непрерывные функции, имеющие ограниченную производную. Заметим, что любая функция из 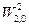 принадлежит пространству
принадлежит пространству 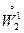 . В этом случае говорят, что имеет место вложение
. В этом случае говорят, что имеет место вложение 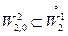 . Для
. Для 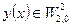 справедливо неравенство
справедливо неравенство
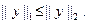
С краевой задачей (1.4), (1.5) связана вариационная задача: среди функций из 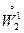 найти ту, что сообщает минимальное значение квадратичному функционалу
найти ту, что сообщает минимальное значение квадратичному функционалу
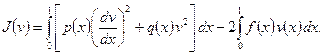 (1.6)
(1.6)
Покажем, что решение задачи (1.4), (1.5) доставляет минимум этому функционалу. Заменив в данном функционале 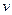 на
на 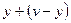 , перепишем его в виде
, перепишем его в виде
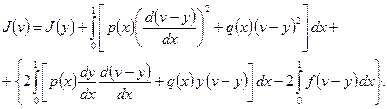
Выражение в фигурных скобках равно нулю. Чтобы увидеть это, следует преобразовать данное выражение с помощью интегрирования по частям и учесть, что 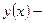 решение задачи (1.4), (1.5). Имеем
решение задачи (1.4), (1.5). Имеем
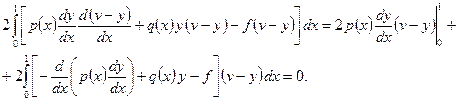
Следовательно:
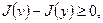
т.е. функция 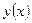 доставляет минимум функционалу (1.6). Верно и обратное: функция
доставляет минимум функционалу (1.6). Верно и обратное: функция 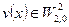 , доставляющая минимум функционалу (1.6), является решением краевой задачи (1.4), (1.5).
, доставляющая минимум функционалу (1.6), является решением краевой задачи (1.4), (1.5).
Подставим в (1.6) функцию вида 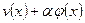 , где
, где 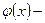 произвольная функция из
произвольная функция из 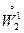 . Тогда
. Тогда 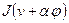 имеет при
имеет при 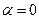 минимум, и, следовательно:
минимум, и, следовательно:
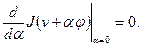
Выражение в левой части этого равенства называется вариацией функционала 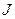 и обозначается
и обозначается 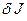 . Вычисления дают
. Вычисления дают
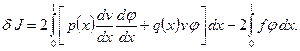
Следовательно:
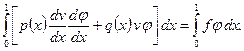 (1.7)
(1.7)
при произвольной функции 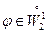 . Проведем интегрирование по частям, получим
. Проведем интегрирование по частям, получим
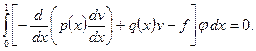
Ввиду того, что  произвольная функция,
произвольная функция, 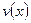 будет удовлетворять уравнению (1.4), а так как
будет удовлетворять уравнению (1.4), а так как 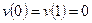 , то
, то 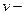 решение краевой задачи (1.4), (1.5). Уравнение (1.4) называется уравнением Эйлера вариационной задачи. Как и уравнение (1.7), оно выражает условие минимума функционала (1.6).
решение краевой задачи (1.4), (1.5). Уравнение (1.4) называется уравнением Эйлера вариационной задачи. Как и уравнение (1.7), оно выражает условие минимума функционала (1.6).
Во многих краевых задачах вариационная постановка является первичной. Она, как правило, следует из физических соображений. Дифференциальное же уравнение является следствием вариационной постановки.
Итак, мы показали, что краевая задача и вариационная равносильны. Отметим важное обстоятельство: вариационная задача равносильна задаче отыскания в пространстве 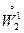 функции, удовлетворяющей уравнению (1.7) при произвольной функции
функции, удовлетворяющей уравнению (1.7) при произвольной функции 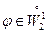 .
.
Уравнение (1.7) было получено из условия равенства нулю вариации функционала. Однако это уравнение можно получить и непосредственно, вне связи с вариационной постановкой из равенства
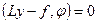
после интегрирования по частям. Такой подход более общий, так можно, например, рассмотреть задачу
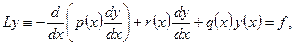
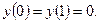
Достоинства вариационной постановки или задачи в виде уравнения (1.7):
- решение вариационной задачи ищется среди более широкого класса функций 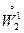 . Это связано с тем, что в функционале и в (1.7) нет вторых производных.
. Это связано с тем, что в функционале и в (1.7) нет вторых производных.
Это обстоятельство можно использовать:
- в численных методах, чтобы искать приближенное решение среди не очень гладких функций (это удобно);
- для расширения понятия решения на те случаи, когда снижены требования на заданные функции, так в (1.7) от 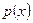 достаточно потребовать ограниченности.
достаточно потребовать ограниченности.
Решение (1.7), принадлежащее 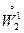 , будем называть обобщенным решением краевой задачи (1.4), (1.5).
, будем называть обобщенным решением краевой задачи (1.4), (1.5).
