Электрические методы на постоянном токе

Горные породы различаются между собой проводимостью 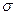, которую следует рассматривать как функцию координат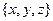

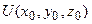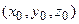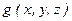Если обозначить – потенциал электрического поля в некоторой точке _, а и 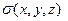распределение источников электрического поля и проводимости как функции координат в объема среды , то связь между этими компонентами определится уравнением:

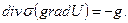(2.31)

Уравнение (31) - основное уравнение, которое описывает электрическое поле постоянного тока.

Из него легко получаем:

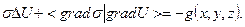(2.32)

Обозначим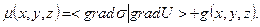

Тогда для потенциала можно записать:

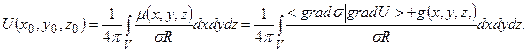
Или

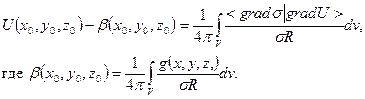
Это уравнение Фредгольмавторого рода, решение которого относительно 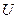по заданным физическим параметрам модели среды: 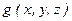и 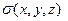можно условно записать в форме:

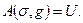(2.33)

Отличие уравнения Фредгольма второго рода от уравнения первого рода по форме состоит в том, что функция 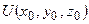, входящая в это уравнение присутствует как во внешнем члене, так и под знаком интеграла. Это обстоятельство имеет далеко идущие математические последствия. Физические последствия связаны с тем, что эффект неоднородности среды оказывается аналогичен возникновению дополнительных - вторичных, связанных с неоднородностями, источников поля. Причем, эти дополнительные источники зависят от градиента поля и градиента проводимости. Чем более неоднородна среда, тем больше градиенты этих величин и тем более проявляется эффект вторичных источников. Поле 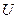реально задано вне области и задача реконструкции модели среды состоит в нахождении по этому – заданному вне области полю либо связанным с ним трансформаций, распределения проводимости внутри области .

То же самое уравнение возникает при описании установившегося теплового режима в предположении, что удельная теплопроводность 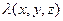– скаляр и не зависит от температуры (следовательно, среда изотропна по тепловым параметрам). Внешние источники тепла (теплогенерация) 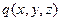не перемещаются и не меняют своих параметров в зависимости от поступившего теплового потока (температура в точках среды - ):

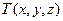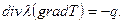
Однако на самом деле, при изучении тепловых потоков приходится предполагать зависимость удельной теплопроводности от температуры и давления, которое в свою очередь влияет на энергетические характеристики системы, внося в нее существенные нелинейности. Например, в [8.1]предполагается зависимость 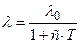. Теплопроводность в зависимости от термобарических условий (P,T), ( которые чаще всего неизвестны), может изменяться в несколько раз, что ведет к рассмотрению результатов моделирования тепловых полей и попыток реконструкции параметров модели среды лишь как оценочных либо, что будет правильней, как эффективных параметров и эффективных моделей

2.5. Динамика движений вещества [6].

В отличие от предшествующих уравнений для физического поля, связывающих параметры модели среды и параметры физического поля, компоненты или трансформации которого наблюдаются уравнения динамики и, прежде всего, геодинамики определяют модели трансформаций физических параметров при тех либо иных процессах. Наблюдаемыми здесь служат современное состояние физической модели, а реконструкции, в зависимости от решаемой задачи, подлежат либо параметры предшествовавшей модели при известных особенностях законов движения (например, параметров вязкости), либо параметры законов движения при гипотезах о характере предыдущих моделей. Есть и еще один, для нас наиболее важный аспект применения законов движения. Это могут быть естественные ограничения на допустимые вариации параметров начальной физической модели в процессе ее реконструкции по наблюдаемым геофизического поля. Это круг вопросов, относящийся к эволюционно динамическим принципам интерпретации геофизических данных.

Основным законом, контролирующим движение вещества, служит закон сохранения массы или уравнение непрерывности:

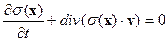(2.34)

.

Здесь 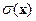- плотность, v – скорость течения, имеющая компонентами .

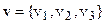Рассмотрим движение флюидовв пористых средах. Для пористых сред закон сохранения имеет близкую форму. Пористая среда характеризуется коэффициентом пористости 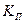, который представляет собой отношение объема пор к общему объему среды, в пределе стремящегося к нулю. Коэффициент пористости является характеристикой среды и, вообще говоря, функцией координат. Закон сохранения массы в этом случае примет вид:

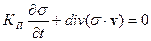(2.35)

При этом следует иметь в виду, что скорость фильтрации и физическая скорость 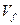потока жидкости не одно и тоже. Они связаны между собой соотношением 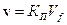. Для получения уравнения движения жидкости в пористой среде приведенный закон необходимо дополнить уравнениями состояния. Они основаны на целом ряде физических допущений.

1. Закон Дарси. В рамках теории линейной фильтрации, описывающей стационарную фильтрацию несжимаемой жидкости 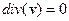, связь между скоростью фильтрацией и давлением 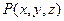задается условием:

.

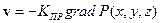Здесь 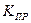- коэффициент проницаемости.

2. Текущая жидкость слабо сжимаема. Это означает, что соотношение между плотностью и давлением определяется соотношением:

,

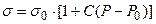где С – коэффициент сжимаемости; 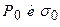- исходные давления и плотность, приложенные в начальный момент времени и зависящие только от пространственных координат; P - текущее давление; σ- плотность, возникшая за счет этого давления. Коэффициент сжимаемости мал в сравнении с единицей и, в результате, 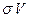мало отличается от 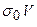. Тогда из закона сохранения массы с учетом закона Дарси после небольших преобразований получаем:

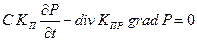(2.36)

3. Изотермическое течение идеального газа.

Уравнение состояния, задающее связь между плотностью и давлением, в этом случае описывается законом Мариотта:

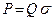
где Q – не зависящая ни от координат, ни от времени константа. Воспользуемся законом сохранения массы и законом Дарси. После подстановок и сокращения на Q получим уравнение газодинамики:

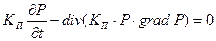(2.37)

Отметим, что в отличие от рассмотренных раннее уравнений, уравнение газодинамики – нелинейно относительно давления.

Уравнения движения вязкой среды - это одна из важнейших геодинамических моделей развития геологических сред. Как всякая модель она пригодна лишь для описания определенных этапов развития – в данном случае эволюционных. В нее не попадают катастрофические события типа формирования глубинных разломов. Но, тем не менее, диапазон ее применимости достаточно широк.

Уравнение движения вязкой среды получается из законов динамики и задается уравнениями Навье - Стокса:

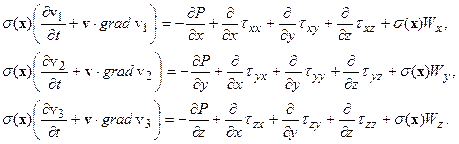(2.38)

Здесь P – давление, W={W_x,W_y,W_z} – вектор массовых сил, а компоненты симметричны относительно тензора вязких напряжений 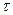связаны с коэффициентом вязкости 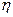и вектором скорости v соотношениями:

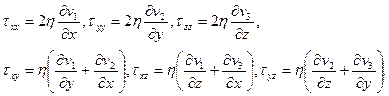
Пренебрегая инерционными (содержащими вторые производные по времени) членами (поскольку течения эти медленны), и рассматривая в качестве массовых сил силы гравитации, из уравнений Навье - Стокса получим:

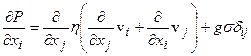
Из этих уравнений видно, что вязкость является определяющим фактором, влияющим на величину скорости перемещений. При моделировании динамики развития геологических объектов она определяется из внешних условий – экспериментов, сопоставления скоростей распространения продольных и поперечных сейсмических волн. Однако распределение этого параметра, оказывая решающее значение на определяемые из уравнений Навье - Стокса скорости перемещений, крайне ненадежно определяется из экспериментальных данных.

Эволюция геологической среды в рамках модели вязких течений– это геодинамические модели сплошной, неструктурированной среды. Она опирается на рассмотрении каждой точки среды как самостоятельно движущейся с той либо иной скоростью. Из этих элементарных движений складываются закономерности движения всего потока. Однако особый интерес представляют более узкие геометрические модели по аналогии с рассмотренными при изучении плотностных моделей в гравиразведке.

Структурные геодинамические моделии уравнения, описывающие их эволюцию, рассматривались в работах Мясникова В.П., В.О. Михайлова (обзор библиографии вопроса приведены в [7 ]), которым мы в основном следуем. В геодинамической модели, в общем виде представляющей собой эволюцию поля скоростей, понятие внутренних границ определяется как поверхности, через которые отсутствует поток масс. Тогда, полная производная по времени для частиц, расположенных на этой поверхности, равна нулю, а последняя, в свою очередь, складывается из пространственной нормальной и частной по времени производных к границам. Это приводит к уравнению равновесия. Дополнительный учет членов, ответственных за денудацию (разрушение, размыв) и осадконакопление в процессе эволюции границ (временной интервал, при котором они служили поверхностью для соответствующих процессов), приводит к уравнениям:

; .

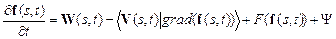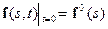(2.39)

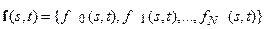- многокомпонентная функция, описывающая эволюцию системы из N+1 геодинамической границы, такой, что в каждый момент времени t глубина границы с номером i в точке s={x,y} равна .

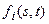Здесь управляющие геодинамические параметры: 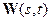- вертикальные составляющие скорости перемещений; 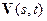- векторы горизонтальных составляющих скоростей перемещений; 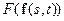- оператор, ответственный за модель денудации рельефа. В работах [3,4] он предлагается пропорциональным лапласиану от уравнения границы с коэффициентом пропорциональности, называемым скоростью размыва, что оправдано для структур с характерным временем развития 10⁶ лет и более; 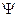- сложная функция, ответственная за дивергентную компоненту в эволюции системы, и определяемая особенностями процессов осадконакопления и метаморфизма. Она зависит от большого числа факторов, включая реологические свойства пород. Попытка полностью реконструировать все законы, определяющие эту компоненту, наталкивается на серьезные проблемы, связанные с отсутствием ясных и обоснованных законов, управляющих процессом ее формирования. Однако, именно в силу сложности, равнозначной многофакторности этой компоненты, среди факторов которой нельзя выделить главные, ее следует рассматривать как отдельное аддитивное слагаемое, определяемое по результатам соответствия моделирования динамических процессов и сопоставления результатов с наблюдаемыми физическими полями.

Анализ модели формирования структур показывает [7], что любая произвольная по рельефу слоев структура может быть получена за счет чисто вертикальных движений, с включением дивергентного члена, а при дополнительно заданных внутренних напряжениях сочетанием дивергентных членов, вертикальных и горизонтальных движений, притом бесконечным множеством способов. Это означает, что процесс денудацииможет быть включен в дивергентный член, ответственный за характер осадконакопления и метаморфизма, и по характеру своего влияния на поведение модели в рамках (39) объединен с вертикальной компонентой действующих нагрузок. В этом случае может быть введена интегрированная математическая модель эволюции структур:

.

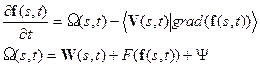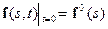(2.40)

2.6. Современная Геодинамика.

Раздел написан по материалам монографии Ю.О. Кузьмина В.С. Жукова [8].

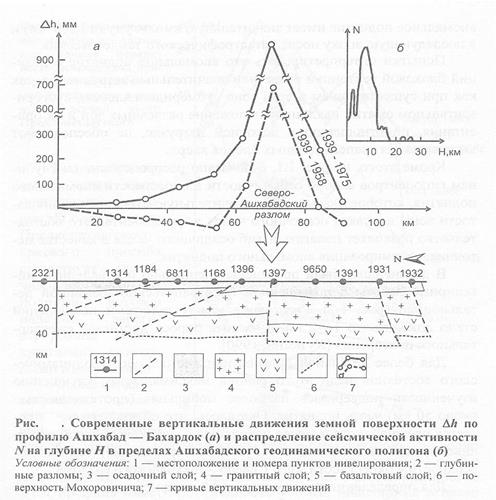
Наряду с глобальными геодинамическими процессами происходивших на протяжении всей истории развития Земли, фрагментированными территориально и по характеру происходящих процессов в тех либо иных пространственно временных масштабах [9], происходили и происходят современные движения поверхности Земли. Первые привели к формированию современных геологических структур и объектов, изучаемых геофизическими методами. Вторые имеют сложную природу и многообразие причин их вызывающих. Они регистрируются многократным проведением нивелировочных работ и измеряются в значениях горизонтальных градиентов движений – мм/км в год.

На фоне региональных современных движений, регистрируемых вдоль линий Государственной сети и составляющих первые единицы Δh( м/км в год) наблюдаются существенно более интенсивные локальные аномалии, как вертикальных, так и горизонтальных движений. Типичный пример в зоне сейсмической активности такого мониторинга приведен на рис. 2.5 (взято из монографии [8]). На этом и многих других примерах выявлено, что интенсивные локальные аномалии вертикальных и горизонтальных движений земной поверхности приурочены к зонам разломов. Их характеристики в главном совпадают как в сейсмоактивных, так и асейсмичных разломных зонах. Однако интенсивность деформаций выше в сейсмоактивных зонах. Их амплитуда составляет 50 – 70 мм/год. Они короткопериодичны (0.1 – 1 год), хорошо локализованы (0.1 – 1 км.). Такого сорта аномалии определены как суперинтенсивные деформации (СД), характерные для зон разломов. Приуроченность СД к разломам очевидно связана с тем, что с точки зрения механики сплошных сред разломы это зоны локальных аномальных физико-механических характеристик геологической среды. В силу повышенной трещиноватости и пониженных прочностных свойств именно эти зоны более подвержены движениям при приложении внешних усилий. Наличие в геологической среде разломов и разрывных нарушений приводит к формированию локального поля деформаций в окрестности включений. Это поле деформаций сложным образом зависит от соотношения упругих констант относительных изменений объемных упругих модулей ( 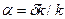), коэффициента Пуассона 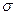, модуля сдвига среды 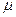, величины тектонического напряжения – изостатического давления 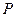. Введя коэффициент

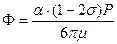, можно записать следующее выражение для компонент вектора смещений:

.

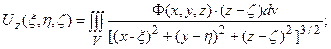
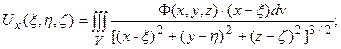
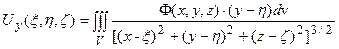Таким образом, формулы расчета компонент 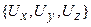вектора смещений 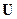, которые являются моделью поля по эффективному параметру среды 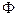, зависящему от упругих констант и приложенных напряжений аналогичны модели взаимодействия для компонент гравитационного поля. В этой связи возможна постановка задачи реконструкции модели среды по заданным результатам геодезического мониторинга - вектора смещений 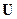. По сути своей эта задача означает нахождение поля напряжений в горных массивах по измеренным уклонениям нивелировочных данных со временем или, что то же самое, по известным деформациям на дневной поверхности.

Выводы

Единство задач извлечения информации из геофизических данных состоит в том, что задана наблюдаемая, либо уже подготовленная процедурами обработки компонента 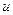физического поля – его атрибуты, оператор , отображающий параметры модели среды 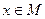в эти данные, считающиеся известными. Задача состоит в нахождении параметров модели среды по заданным данным и заданному оператору. Это задача условно может быть записана в виде

.

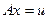Это операторное уравнение первого рода. В разных методах и на разных стадиях обработка, решение обратных геофизических задач, решение задач геофизической интерпретации, компоненты задачи 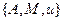могут быть различны, и принимать совершенно разные формы. Однако неизменным остается возможность ее общего представления в виде операторного уравнения первого рода и необходимость создания корректных методов его решения.

Литература, приводимая в списке для настоящей главы, ни в коей мере не служит перечнем требуемых для изучения содержательных задач учебников. Мы считаем, что учебники по сейсморазведке, гравиразведке и другим методам – уже изучены и есть. Приводимый список относится к частным вопросам и особенностям.

Литература

1 Терещенко С.А. Методы вычислительной томографии. – М. ФИЗМАТЛИТ, 2004 – 320с.- ISBN 5-9221-0551-5;

2.Наттерер Ф. Математические аспекты компьютерной томографии:- М. Мир, 1990.- 288 с

3. Gerveny V, Molotkov I.A., Psenkik I. Ray method in seismology. Praha – Univerzita Karlova, 1977. – P.214.

4.Гольдин С.В. Интерпретация данных сейсмического метода отраженных волн. – М.: Недра, 1979. – 380с.

5. Сейсмическая томография. Под ред. Г. Нолета. М. Мир, 1990.- 416 с.

6. Г.Дюво., Ж.-Л.Лионс. Неравенства в механике и физике.
М.: Наука, 1980.-382 с

7. Михайлов В.О. и др. Геодинамические модели и их применение при совместной интерпретации геологических и геофизических данных (обзор). Физика Земли, 2007,№1б с. 4-15.

8. Ю.О. Кузьмин В.С. Жуков Современная геодинамика и вариации физических свойств горных пород. Москва, Издательство Московского Государственного Горного Университета, 2004.262 С.

9. С.В. Аплонов Геодинамика. Учебник. – СП-б Из-во С-Петерб. Ун-та, 2001. – 360 с.