Разработка математической модели измерений диэлектрической проницаемости и проводимости контролируемых сред в широком диапазоне частот

РЕФЕРАТ

Отчет 17 с., 4 рис., 0 табл., 17 источн.

НАНОМАТЕРИАЛЫ, ЭЛЕКТРОМАГНИТНЫЕ ПАРАМЕТРЫ, ПРОВОДИМОСТЬ, ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ, МАГНИТНАЯ ПРОНИЦАЕМОСТЬ, ЭКСПРЕСС ДИАГНОСТИКА, ПРИБОР, МЕТРОЛОГИЧЕСКОЕ ОБЕСПЕЧЕНИЕ

Объектом исследования являются методы и устройства экспресс – диагностики электромагнитных параметров наноматериалов.

Целью работы является решение проблемы обеспечения возможности проведения экспресс-диагностики электромагнитных параметров радиопоглощающих наноматериалов, полупроводниковых наногетероструктур и углеродных наноматериалов, а также их метрологическое сопровождение. В проекте планируется разработать метод экспресс-диагностики электромагнитных параметров углеродных наноматериалов методом импульсного электромагнитного зондирования контролируемых объектов, а также создать экспериментальный образец установки экспресс-диагностики параметров наноматериалов.

ВВЕДЕНИЕ

Согласно аспирантскому плану на первый год обучения, по теме научного исследования «Бесконтактные устройства оперативного контроля электромагнитных параметров наноматериалов», должна быть получены следующие результаты:

· Создание математической модели процедуры обработки измерительной информации при экспресс – диагностике наноматериалов.

· Выступление на конференции: «Современные достижения в области создания перспективных неметаллических композиционных материалов и покрытий для авиационной и космической техники», ФГУП «ВИАМ» ГНЦ РФ ,Москва, декабрь 2015г

· Подана на рецензирование в журнал «Вестник СГАУ» статья «Устройства и методы диагностики электромагнитных параметров тонких пленок и наноматериалов» .

К сожалению поданная на рецензирование статья «Устройства и методы диагностики электромагнитных параметров тонких пленок и наноматериалов» была отклонена. Планируется доработка данной статьи с последующим публикованием.

Ниже представлен раздел, посвященный разработке части математической модели процедуры обработки измерительной информации при экспресс – диагностике наноматериалов.

Наноматериалы широко используются в радиотехнике для создания полупроводниковых наногетероструктур, углеродных наноматериалов, а также радиопоглощающих покрытий, в частности, для разработки комплекса методов снижения заметности летательных аппаратов в радиолокационном, инфракрасном и других областях спектра. Свойства поглощения и отражения радиоволн зависят от электромагнитных свойств материала покрытия – проводимости, диэлектрической и магнитной проницаемостей, которые необходимо оперативно контролировать как в процессе отработки технологии производства, так и в режимах оценки качества готовых покрытий. Наноматериалы, в частности углеродные, применяются также для создания принципиально новых систем антиобледенения летательных аппаратов, где оперативный контроль электромагнитных свойств также выжжен и актуален.

Современные методы контроля электромагнитных параметров носят разрозненный характер, когда исследуются отдельно электрические (проводимость, диэлектрическая проницаемость) и магнитные (магнитная проницаемость) свойства исследуются на разных установках, требуют принципиально разных конструкций измерительных устройств. В современной теории нет единой математической модели, комплексно описывающей электродинамические параметры наноматериалов в их взаимосвязи, что тормозит данное направление технологического развития.

В литературе практически отсутствуют сведения о метрологическом обеспечении методов и устройств экспресс – диагностики электромагнитных параметров наноматериалов. Определение предельных метрологических характеристик разработанных методов и устройств, связанных с исследованием основных, в частности методических и инструментальных, а также дополнительных погрешностей является важной составляющей проекта. Такие исследования определяют требования к комплектующему оборудованию разрабатываемого прибора по точности и условиям эксплуатации и непосредственно влияют на его конструкцию.

РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ИЗМЕРЕНИЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И ПРОВОДИМОСТИ КОНТРОЛИРУЕМЫХ СРЕД В ШИРОКОМ ДИАПАЗОНЕ ЧАСТОТ

Известно [3, 5, 10, 12], что диэлектрическая и магнитная проницаемости материалов есть комплексные величины и определяются формулами , .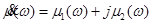

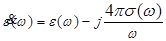Любая среда характеризуется строго определенной совокупностью параметров μ, 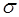, , 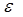законы изменения которых не являются произвольными, а определяются общими законами распределения электромагнитных волн, т.е. уравнениями Максвелла, точнее вытекают из них. Так как скорость распространения электромагнитных волн в любой среде ограничена скоростью света, то очевидно параметры μ, 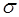, 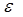взаимозависимы, то есть изменение какого-либо одного параметра влечет за собой изменение других. 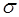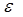Выявим общие законы изменения μ, и от частоты, в диапазоне 0 ÷10¹³ Гц, а также взаимозависимости друг от друга указанных параметров. 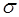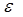В литературе [1, 2, 4, 9, 10, 12, 13-17] имеются сведения об исследовании частотных законов изменения μ, и , на различных уровнях - макроскопическом, микроскопическом, электронном и квантовом. Эти исследования недостаточно полны, весьма разрозненны, проведены для отдельных видов сред (газов, жидкостей, твердых тел), для отдельных участков частот с различными, часто противоречивыми допущениями. Известны также интегральные формулы Крамерса-Кронига [1, 3], показывающие общую частотную взаимосвязь 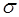и 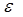, а также 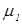и 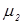. Однако, они носят слишком общий характер, неудобны, так как содержат несобственные интегралы и их применение затруднено для конкретных числовых значений. Кроме того, формулы Крамерса-Кронига не учитывают взаимосвяз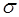и и 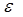с магнитной проницаемостью, хотя, как показывают эксперименты, такая зависимость существует. 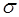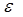Попробуем обобщить экспериментальный и теоретический материал по исследованию зависимостей параметров μ, и от частоты в диапазоне 0 ÷ 10¹³ Гц, для широкого класса сред и материалов без каких-либо дополнительных допущений, кроме тех, которые накладываются на общую максвелловскую макроскопическую теорию электромагнитного поля. Анализ результатов опубликованных экспериментальных и теоретических исследований, показал, что зависимост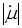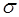и , и 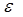различных сред от частоты в диапазоне 0 - 10¹³ Гц имеют вид, показанный на рисунках.1.1 - 1.3.

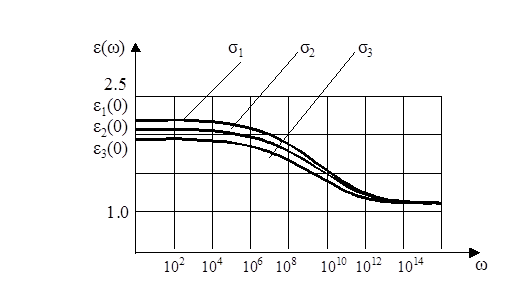Рисунок 1.1 - График зависимости удельной электрической проводимости наноматериалов от частоты

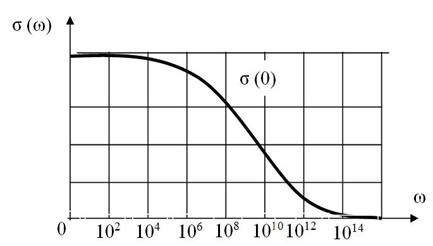
Рисунок 1.2 - График зависимости диэлектрической проницаемости углеводородных топлив от частоты для различных проводимостей, σ₁ > σ₂ > σ₃

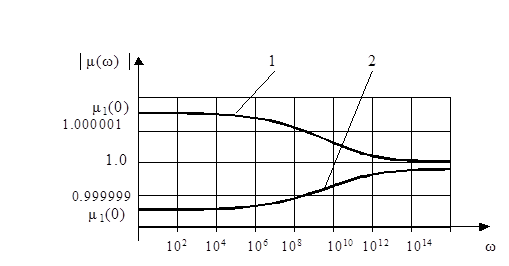Рисунок 1.3 - График зависимости магнитной проницаемости углеводородных топлив от частоты: 1 – парамагнетики, 2- диамагнетики

Удельная электрическая проводимость с ростом частоты асимптотически стремится к нулю. Относительная диэлектрическая проницаемость асимптотически стремится к единице. Причем, чем больше проводимость среды, тем выше ее диэлектрическая проницаемость. Модуль относительной магнитной проницаемости также асимптотически стремится к единице, только для диамагнитных сред 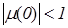, а для парамагнитных сред 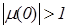(рисунок 8.1). Анализ графиков и дополнительные исследования показали, что зависимость проводимости от частоты (рис.1.1) для различных сред с высокой степенью точности аппроксимируется выражением :

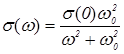, (1.1)

где 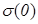- проводимость вещества при ,

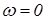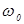- некоторая постоянная, присущая данному веществу, наряду с другими характеризующая его электродинамические свойства.

В общем случае проводимость и диэлектрическая проницаемость веществ на различных частотах связаны формулами Крамерса-Кронига, которые в наиболее удобном виде записываются следующим образом [17]:

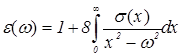, (1.2)

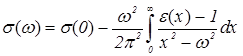, (1.3)

где 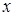- формальный параметр интегрирования, который в функциях 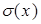и 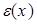нужно понимать как частоту.

Черта на интеграле означает, что берется его главное значение. Подставляя в (1.2) формулу (1.1) и заменяя 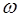на 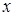, получим аналитическую зависимость диэлектрической проницаемости от частоты:

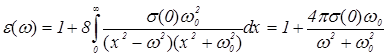, (1.4)

Анализ этого выражения подтверждает соответствие его известным экспериментальным данным, приведенным на рисунке 1.3. Для аналитической проверки полученной зависимости подставим выражение (1.4) в (1.3).

,

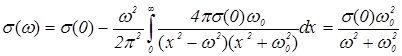то есть получили (2.119), что наряду с экспериментальными данными также подтверждает правильность аналитических зависимостей (8.1) и (8.4). При 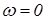имеем :

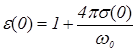. (1.5)

Отсюда находим:

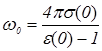. (1.6)

По формуле (1.1) можно определить характеристическую частоту 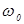для любого материала по известным значениям 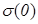и 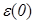. Здесь во всех формулах проводимость выражена в системе СГСЭ, т.е. в [ 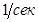]. Подставляя (1.6) в выражения (1.1) и (1.4), получим формулы для вычисления проводимости и диэлектрической проницаемости на различных частотах.

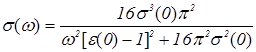, (1.7)

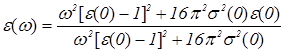, (1.8)

Формулы (1.7) и (1.8) имеют большое практическое значение, так как позволяют по известным 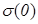и 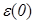определять значения 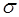и 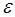на любых частотах, в том числе на СВЧ и инфракрасных, прямые измерения на которых затруднены, требуют специальной аппаратуры и метрологически плохо обеспечены (погрешность 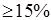). В нашем случае достаточно знать значения 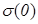и 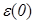, измерение которых не вызывает затруднений и обеспечено высокоточной стандартной аппаратурой. Исключая из (1.1) и (1.4) частоту 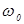получим формулу взаимозависимости относительной диэлектрической проницаемости от удельной проводимости материала, на любой частоте

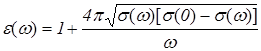, (1.9)

Из (1.5) и (1.9) видно, что при 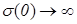, 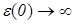. Это полностью подтверждается экспериментом, а также данными литературы [43, 44, 46, 48, 49, 52, 59 - 65]. Выразим из (8.1) 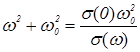и подставим в (1.4) :

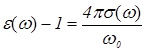. Подставляя сюда вместо 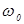выражение (1.6), получим

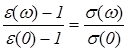, (1.10)

Формула (1.10) показывает взаимосвязь удельной проводимости и диэлектрической проницаемости на произвольных частотах.

Анализ опубликованных экспериментальных и теоретических данных показал, что действительную часть 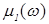комплексной магнитной проницаемости 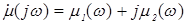, можно описать функцией:

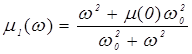, (1.11)

где 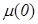- магнитная проницаемость среды при .

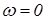Тогда по формуле Крамерса-Кронига получаем :

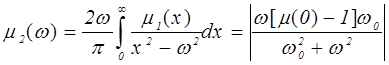, (1.12)

Отметим, что мнимая часть магнитной проницаемости, как и проводимость, определяет поглощение (диссипацию) энергии в веществе (магнитные потери). Поэтому в (1.12) берется модуль, так как 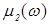всегда должна быть больше нуля. Модуль магнитной проницаемости определяется :

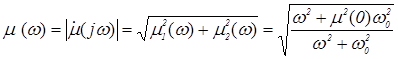, (1.13)

что полностью соответствует рисунку 1.3. При 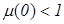, среда является диамагнитной, при 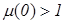- парамагнитной (ферромагнитной), при 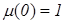- вакуум. Выражения (1.11) - (1.13) учитывают все известные авторам сведения об этих параметрах. В частности 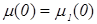; ; 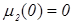; 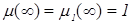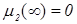, при этом 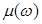; 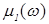- четные, а 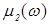- нечетная функция частоты. Подставив в (1.11) - (1.13) вместо 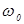выражение (1.6), получим :

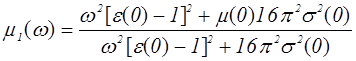, (1.14)

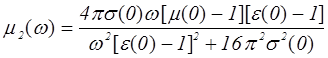, (1.15)

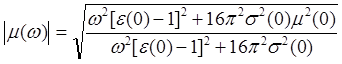, (1.16)

Выражения (1.14)- (1.16) аналогично (1.7) и (1.8), позволяют определять значение магнитной проницаемости и ее составляющих на любых частотах, в том числе на СВЧ, по известным значениям 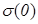; ; 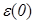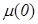, измерение которых не вызывает затруднений. Выразим из (8.11) 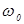и подставим в (1.12):

,

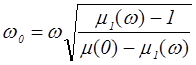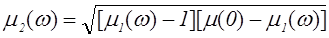, (1.17)

Формула (1.17) позволяет вычислить функцию 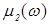по известной 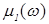и показывает их взаимосвязь. Выразим из (1.1): 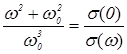и подставим в (1.17): 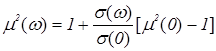. Отсюда получаем:

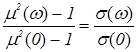, (1.18)

Выражение (1.18) показывает взаимосвязь магнитной проницаемости и удельной электрической проводимости среды. Учитывая (1.10) получим :

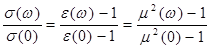, (1.19)

Формула (1.19) показывает общую взаимосвязь основных электродинамических параметров среды. Соотношение (1.19) подтверждается экспериментальными исследованиями, проведенными для различных жидких, газообразных и сыпучих сред. Измерения проводились с помощью воздушного конденсатора и катушки индуктивности, помещаемых в исследуемую среду [13]. Эксперимент подтвердил качественный вид приведенных зависимостей и с погрешностью 12% совпал с формулой (1.19) по количественным оценкам. Нет каких-либо теоретических предпосылок запрещающих распространение полученных результатов на диапазон частот до 10¹³ Гц. , тем более, что для большинства материалов магнитная проницаемость становится равной 1 и не зависит от частоты уже на частотах, гораздо более низких, чем оптические [10]. При более высоких частотах длина волны электромагнитного излучения становится соизмеримой с размерами молекул и атомов, что приводит к невыполнению соотношения (1.19), так как на этих частотах имеют место колебания кристаллической решетки (инфракрасный диапазон) и колебания электронов (ультрафиолетовый диапазон), влияющие на диэлектрическую и магнитную поляризацию вещества [2]. На оптических частотах понятие электрической проводимости принимает более общий характер и может пониматься как интегральный параметр, характеризующий квантово-механические процессы , связанные с поглощением среды. В этом случае в полученных выражениях под проводимостью σ(ω) следует понимать параметр, образующий мнимую часть комплексной диэлектрической проницаемости [3]. На оптических частотах общий характер изменения составляющих комплексной диэлектрической проницаемости иллюстрируется рисунком 1.4 [5].

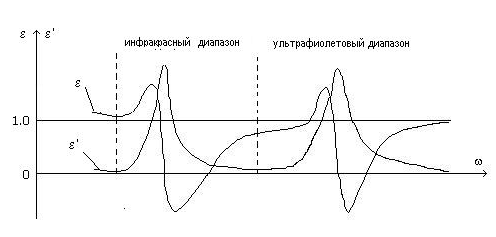Рисунок 1.4 - Изменение составляющих комплексной диэлектрической проницаемости материалов от частоты в оптическом диапазоне

На оптических частотах диэлектрическая проницаемость и проводимость определяют коэффициенты оптического преломления и поглощения среды, которые рассмотрены в предыдущем разделе данной работы.

Соотношение (1.19) описывает объективно существующую закономерность, характеризующую фундаментальные электрические и магнитные свойства материалов и сред в диапазоне частот 0-10¹³ Гц. Формулы (1.7), (1.8), (1.16), (1.18) позволяют определить значения 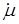, , 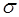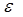на различных частотах, проводя измерения на какой-либо одной частоте. Полученные результаты дают возможность более точно рассчитывать и анализировать распространение электромагнитных волн в разнообразных средах, а также более точно рассчитывать и конструировать датчиковую аппаратуру, основанную на использовании изменений параметров 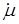, , 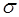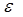. В частности полученные соотношения могут быть использованы при измерении электромагнитных параметров наноматериалов.

В заключение раздела отметим, что рассматриваемые электродинамические параметры определяют фазовую и групповую скорости распространения электромагнитного сигнала в среде, волновое сопротивление среды, коэффициент поглощения, коэффициент преломления по формулам (1.16) – (4.20). Отметим, что вся теория раздела написана для абсолютных значений диэлектрической и магнитной проницаемостей ε_А= ε_оε, μ_А= μ₀μ , где ε₀=8.85416·10^-12 [Ф/м], μ₀=1.256637·10^-6 [Гн/м], что следует из размерностей и физического смысла. Однако, индекс «а» для указанных параметров в разделе 4.1 отсутствует, как это принято при записи уравнений Максвелла. Из (4.19) следует, что при 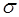=0, то есть для среды без поглощения, можно записать:

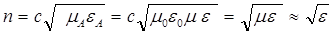. (1.20)

Последнее равенство следует из того, что 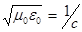, μ ≈ 1 для жидких нефтепродуктов. Из рисунка 1.4 видно: диэлектрическая проницаемость может быть отрицательной, поэтому даже при σ =0 обладать свойствами поглощения, что имеет место на оптических частотах.

Формулы (1.7), (1.8), (1.16), (1.19) определяют математическую модель измерения, по которой могут быть реализованы различные варианты построения измерительной процедуры.

ЗАКЛЮЧЕНИЕ

В результате исследований получены следующие выводы.

1. Полученные результаты на основе созданной математической модели дают возможность более точно рассчитывать и анализировать распространение электромагнитных волн в разнообразных средах, а также более точно рассчитывать и конструировать датчиковую аппаратуру, основанную на использовании изменений параметров проводимости, диэлектрической и магнитной проницаемости.

Выведены формулы определяющие математическую модель измерения, по которой могут быть реализованы различные варианты построения измерительной процедуры.