Расчет токов во всех ветвях цепи гармонического тока
Расчет электрической цепи на гармоническом токе
Составление системы уравнений по законам Кирхгофа
Для цепей гармонического тока уравнения Кирхгофа могут быть записаны в двух формах:
а) для мгновенных значений токов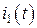 
, 
, 
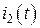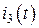(в виде временных функций);
б) для комплексных амплитуд токов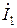 
, 
, 
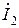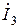или комплексных действующих значений токов 
, 
, 
:
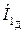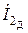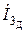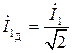, (2.1.1)
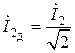, (2.1.2)
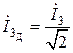. (2.1.3)
Чтобы записать уравнения первого и второго законов Кирхгофа для анализируемой цепи рис. 1.1, обозначим направления токов 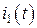, , 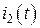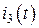в ветвях этой цепи (см. рис. 2.1.1).
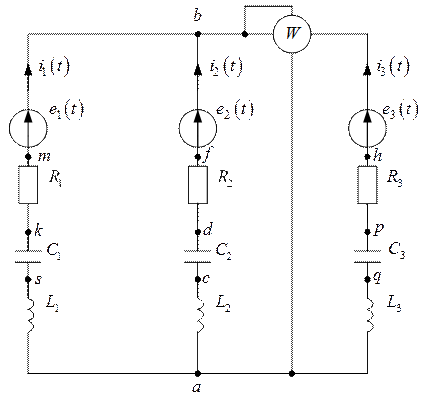
Рис. 2.1.1. Схема анализируемой цепи с обозначенными на ней направлениями токов ветвей
Для анализируемой схемы рис. 2.1.1 для мгновенных значений (в виде временных функций) можно записать два уравнения второго закона Кирхгофа и одно уравнение первого закона Кирхгофа. Обходя каждый из контуров цепи рис. 2.1.1 по часовой стрелке, а также беря втекающие в узел ”b” токи ветвей со знаком “плюс”, получим систему уравнений:
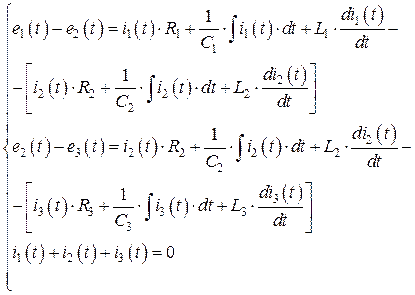. (2.1.4)
Поскольку решать такую систему интегро-дифференциальных уравнений сложно, переходят к использованию метода комплексных амплитуд. При этом записываются комплексные амплитуды токов, напряжений и комплексные сопротивления пассивных элементов (сопротивлений, ёмкостей, индуктивностей), что позволяет перейти к системе комплексных алгебраических уравнений. Такая система для нашей схемы будет иметь вид:
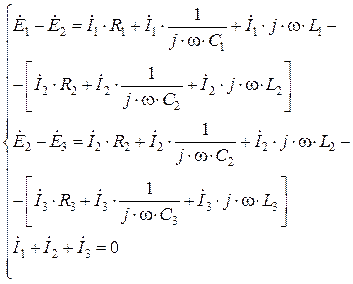, (2.1.2)
где: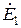 
, 
, 
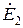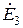– комплексные амплитуды источников ЭДС гармонического тока 
, 
, 
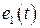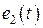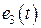, соответственно, [В]; , 
, 
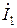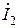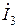– комплексные амплитуды искомых гармонических токов ветвей 
, 
, 
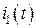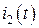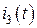, соответственно, [А]; 
, 
, 
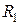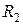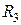– активные сопротивления ветвей схемы рис. 2.1.1, [Ом]; 
, 
, 
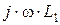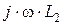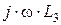– комплексные (реактивные) сопротивления индуктивностей ветвей схемы рис. 2.1.1, [Ом]; 
, 
, 
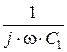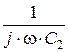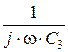– комплексные (реактивные) сопротивления ёмкостей ветвей схемы рис. 2.1.1, [Ом]; ( подробнее см. [5, 6]).
Расчет токов во всех ветвях цепи гармонического тока
Как и ранее для цепей с источниками постоянного тока, расчет электрической цепи с источниками гармонического тока можно проводить одним из следующих способов:
– использованием непосредственно законов Кирхгофа;
– методом контурных токов (МКТ);
– методом узловых потенциалов (МУП);
– методом эквивалентного генератора (МЭГ), включающим, при необходимости, метод преобразования треугольника в звезду.
Прежде всего, выберем наиболее рациональный из перечисленных методов расчета. При использовании системы уравнений (2.1.2), составленных по законам Кирхгофа, число этих одновременно решаемых уравнений будет равно числу неизвестных токов ветвей, то есть, трем. При использовании метода контурных токов число уравнений системы будет равно числу контурных токов, то есть, для нашей схемы это два. При использовании же метода узловых потенциалов, число уравнений будет равно числу независимых узлов, то есть, одному (при этом один из узлов необходимо заземлить). Таким образом, наиболее эффективно решать поставленную задачу, используя метод узловых потенциалов. Дополнительным преимуществом при этом будет то, что проверять результаты расчета, проведенного методом узловых потенциалов, следует уравнениями первого законы Кирхгофа, то есть, такая проверка наиболее проста.
Использование метода эквивалентного генератора в данном случае также сводится к вопросу об использовании законов Кирхгофа, МКТ или МУП, так как в МЭГ также придется определять токи во всех ветвях цепи.
Таким образом, для нашего случая наиболее рациональным является использование метода узловых потенциалов, для чего следует составить соответствующее уравнение метода узловых потенциалов для рассчитываемой схемы рис. 2.1.1. Для этого, перерисуем схему рис. 2.1.1 с учетом необходимости заземления одного из узлов схемы (пусть это будет, например, узел “a”) и с учетом того, что гармонические ЭДС и искомые токи представлены для удобства расчета в комплексной форме. Тогда схема примет вид, показанный на рис. 2.2.1. Заметим, что заземление узла “a” означает, что его потенциал принят равным нулю, то есть, выполняется условие:
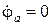, (2.2.1)
где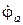 
– комплексное значение потенциала узла “a”, [В].
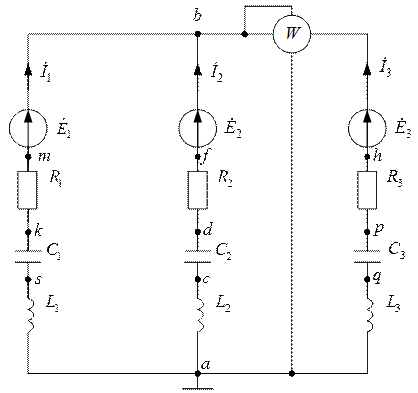
Рис. 2.2.1. Схема анализируемой цепи с заземленным узлом “a”
Составление уравнения метода узловых потенциалов для анализируемой цепи рис. 2.2.1 начнем со следующего рассуждения. Если бы нам были известны комплексные амплитуды потенциалов точек “a” и ”b” 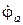и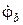 
, соответственно, то токи ветвей можно было бы легко найти, так как ток ветви равен комплексной амплитуде падения напряжения на ветви 
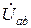(разности потенциалов между точками “a” и ”b” схемы рис. 2.2.1), деленной на комплексное сопротивление соответствующей ветви, с учетом комплексной амплитуды напряжения источника, расположенного в этой ветви. Далее для упрощения изложения мы будем оперировать понятием “комплекс” тока или напряжения, имея в виду его “комплексную амплитуду”. Итак, комплексы токов ветвей равны:
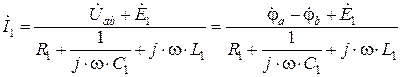, (2.2.2)
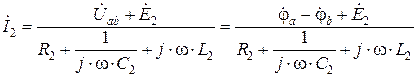, (2.2.3)
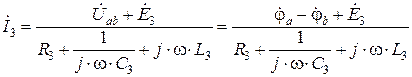. (2.2.4)
Если эти выражения (2.2.2) – (2.2.4) подставить в выражение первого закона Кирхгофа – третье уравнение системы (2.1.2), то можно получить уравнение метода узловых потенциалов для анализируемой схемы рис. 2.2.1:
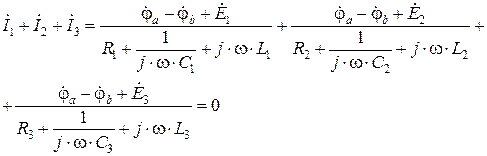. (2.2.5)
Учитывая нулевой потенциал узла “a” схемы рис. 2.2.1 (выражение (2.2.1)), получим:
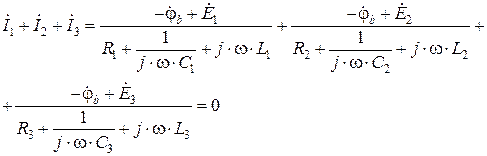. (2.2.6)
Введем вспомогательные обозначения комплексных проводимостей первой, второй и третьей ветвей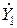 
, 
, 
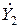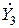, соответственно:
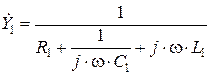, (2.2.7)
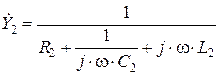, (2.2.8)
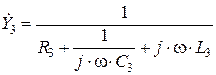. (2.2.9)
Выражая из (2.2.6) потенциал узла ”b” схемы рис. 2.2.1, с учетом обозначений (2.2.7) – (2.2.9), имеем:
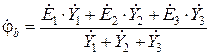. (2.2.10)
Подставив численные значения комплексов в выражение (2.2.10), получим комплексное значение 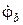потенциала точки ”b” схемы рис. 2.2.1. После этого легко найти комплексы токов ветвей из выражений (2.2.2) – (2.2.4).
Проверку результатов расчета схемы рис. 2.2.1, проведенного методом узловых потенциалов, следует осуществить подстановкой полученных численных значений комплексов токов ветвей в уравнение первого закона Кирхгофа – третье уравнение системы (2.1.2). Допустимая относительная погрешность расчетов составляет 5%.