| f(t) = L-1[X(p)]×1(t) | X(p) = L[f(t)] | X(z) ( 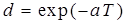 ) ) |
| d(t) | | – |
| 1(t) | 1/p | 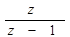 |
| t | 1/p2 | 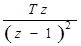 |
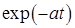 | 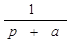 | 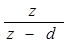 |
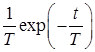 | 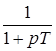 | |
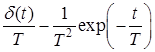 | 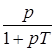 | |
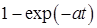 | 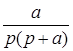 | 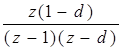 |
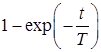 | 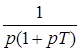 | |
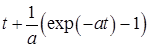 | 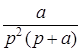 | 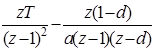 |
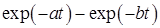 | 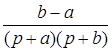 | 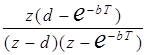 |
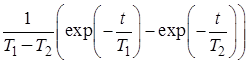 | 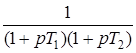 | |
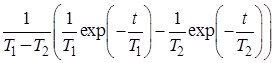 | 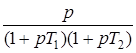 | |
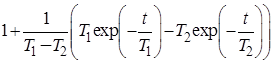 |  | |
 |  | |
 | 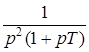 | |
| f(t) = L-1[X(p)]×1(t) | X(p) = L[f(t)] | X(z) ( 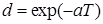 ) ) |
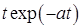 | 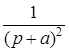 | 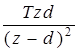 |
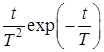 | 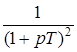 | |
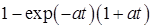 | 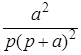 | 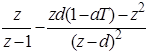 |
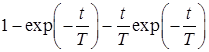 | 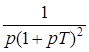 | |
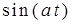 | 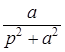 | 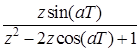 |
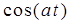 | 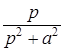 | 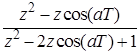 |
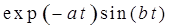 | 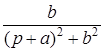 | 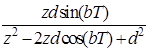 |
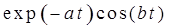 | 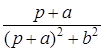 | 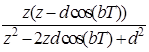 |
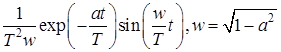 | 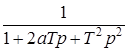 | |
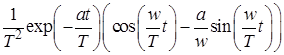 | 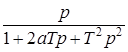 | |
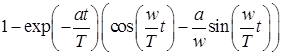 | 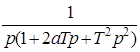 | |
Приложение 2
Основные характеристики типовых динамических звеньев РАС
| ПФ и схема звена | Переходная характеристика | ЛАЧХ и ЛФЧХ |
| 1. Апериодическое звено первого порядка |
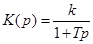 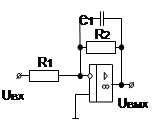 | 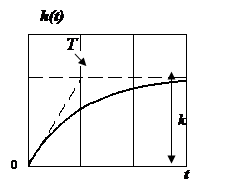 |  |
| 2. Безынерционное звено |
K(p) = k  | 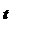  |    |
| 3. Колебательное звено |
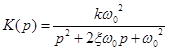 | 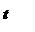 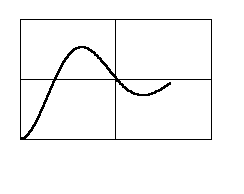 | 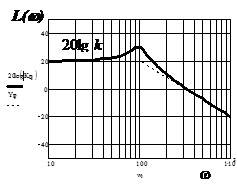  |
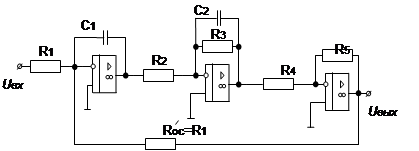 |
| 4. Апериодическое звено второго порядка |
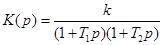 |   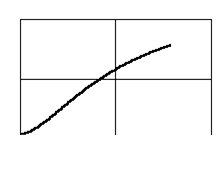 |  |
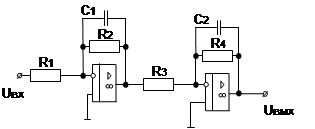 |
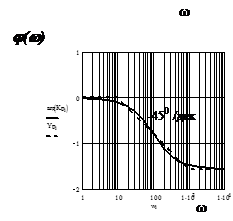
| 9. Изодромное звено |
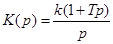  | 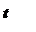 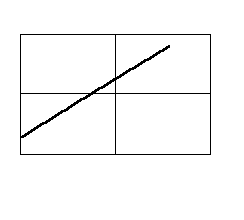 |   |
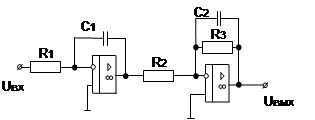
 10. Интегрирующее звено с замедлением (инерционное интегрирующее) 10. Интегрирующее звено с замедлением (инерционное интегрирующее) |
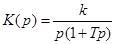 | 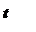  | 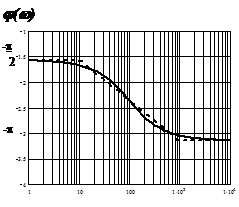 |
 |
Приложение 3
Некоторые формулы для вычисления дисперсии
Если спектральная плотность Sх(ω) описывается дробно-рациональ-ной функцией относительно ω, то для вычисления Dx получаем формулу
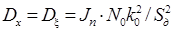 ®
® 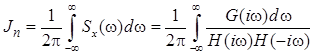 . (П.1)
. (П.1)
где 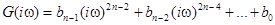 – полином, содержащий четные степени iω до 2n – 2 включительно; а
– полином, содержащий четные степени iω до 2n – 2 включительно; а 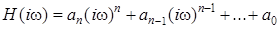 – полином степени n, корни которого лежат в верхней полуплоскости комплексной переменной ω.
– полином степени n, корни которого лежат в верхней полуплоскости комплексной переменной ω.
Значения интегралов (П.6) при n ≤ 4 вычисляются по формулам:
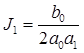 ,
, 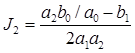 ,
, 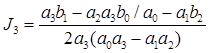 ,
,
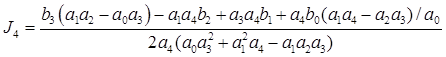 . (П.2)
. (П.2)
Приложение 4
Некоторые формулы для определения
эффективной шумовой полосы fэф по ПФ разомкнутой системы W(p).
Под эффективной шумовой полосой понимается величина, равная полосе пропускания эквивалентной РАС с прямоугольной АЧХ, с одинаковой с исходной РАС ПФ на нулевой частоте и одинаковой дисперсией выходного процесса при действии на входах этих систем белого шума.
Зная fэф , можно сразу определить дисперсию РАС:
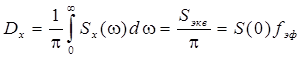 . (П.3)
. (П.3)
Таблица П.4.1
| W(p) | fэф |
| k/p или k/p(1+pT) | 0,5k |
| k/(1+pT) | 0,5k2/(T(1+k)) |
| k/(p(1+pT1)(1+pT2)) | 0,5k(T1+T2)/(T1+T2 – kT1T2) |
| k(1+pT2)/(p(1+pT1)(1+pT3)) | 0,5k(T1+kT22+T3)/(T1+T3+k(T1T2+T2T3 –T1T3)) |
| k(1+pT2)/(p(1+pT1)) | 0,5k(T1+kT22)/(T1+kT1T2)=0,5k(1+kT2T2/T1)/(1+kT2) |
| k(1+pT)/p2 | 0,5(1+kT2)/T |
Приложение 5
Некоторые формулы для вычисления коэффициентов ошибок
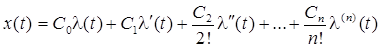 . (П.4)
. (П.4)
ПФ замкнутой системы по ошибке
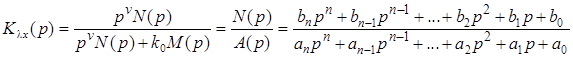 , (П.5)
, (П.5)
Формулы для вычисления коэффициентов ошибок (П.5):
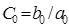 ,
, 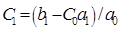 ,
, 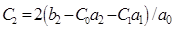 ,
, 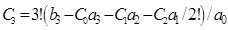 ,
,
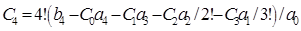 ,
, 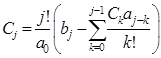 . (П.6)
. (П.6)
Формулы для вычисления коэффициентов ошибок по ПФ разомкнутой системы с порядком астатизма v ( 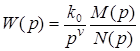 ).
).
Полином числителя M(p) имеет вид 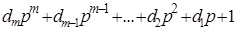 .
.
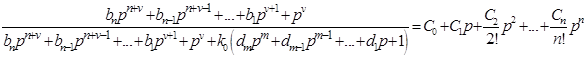 . (П.7)
. (П.7)
v = 0. 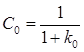 ,
, 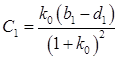 ,
, 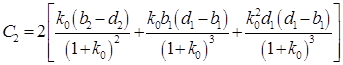 .
.
v = 1. 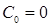 ,
, 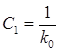 ,
, 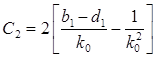 .
.
v = 2. 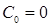 ,
, 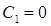 ,
, 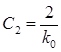 . (П.8)
. (П.8)
Редактор Г. А. Солопова
Компьютерная верстка – Е. В. Беспалова
ИД № 06039 от 12.10.2001 г.
Сводный темплан 2009 г.
Подписано в печать14.07.09 . Формат 60×84 1/16. Бумага офсетная.
Отпечатано на дупликаторе. Усл. печ. л. 5,75. Уч.-изд. л. 5,75.
Тираж 150 экз. Заказ 519.
_________________________
Издательство ОмГТУ. 644050, г. Омск, пр. Мира, 11; т. 23-02-12
Типография ОмГТУ
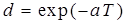 )
) 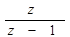
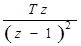
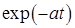
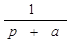
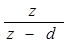
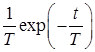
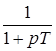
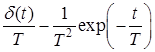
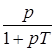
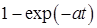
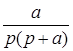
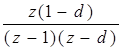
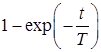
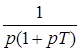
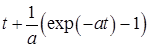
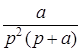
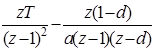
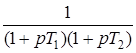
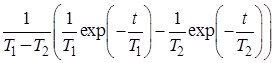
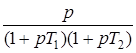
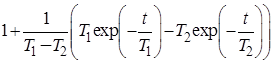
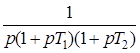
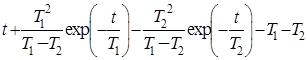
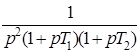
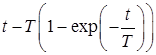
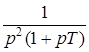
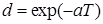 )
) 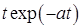
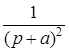
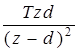
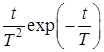
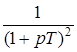
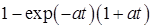
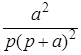
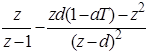
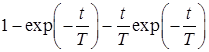
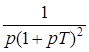
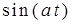
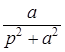
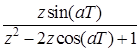
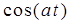
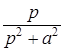
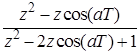
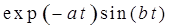
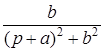
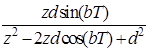
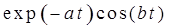
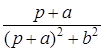
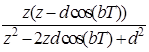
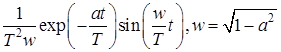
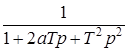
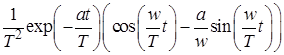
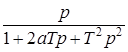
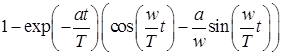
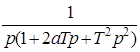
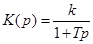




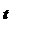


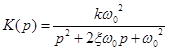




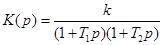







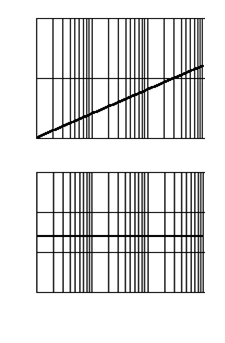
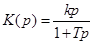
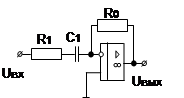

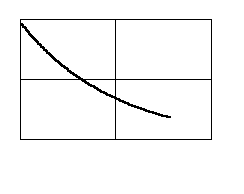

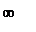



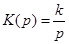
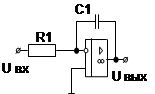
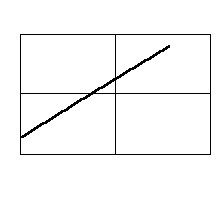
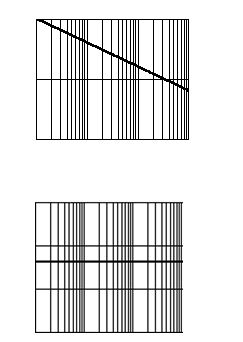
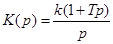

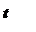



 10. Интегрирующее звено с замедлением (инерционное интегрирующее)
10. Интегрирующее звено с замедлением (инерционное интегрирующее) 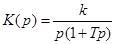
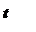



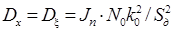 ®
® 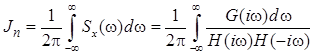 . (П.1)
. (П.1)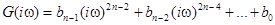 – полином, содержащий четные степени iω до 2n – 2 включительно; а
– полином, содержащий четные степени iω до 2n – 2 включительно; а 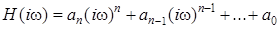 – полином степени n, корни которого лежат в верхней полуплоскости комплексной переменной ω.
– полином степени n, корни которого лежат в верхней полуплоскости комплексной переменной ω.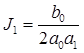 ,
, 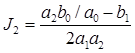 ,
, 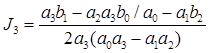 ,
,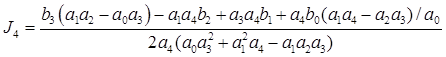 . (П.2)
. (П.2)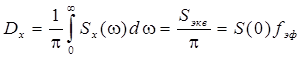 . (П.3)
. (П.3)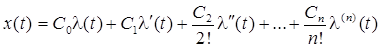 . (П.4)
. (П.4)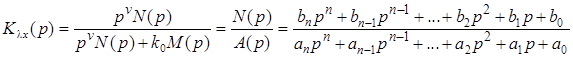 , (П.5)
, (П.5)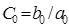 ,
, 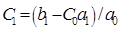 ,
, 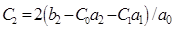 ,
, 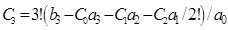 ,
,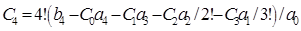 ,
, 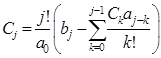 . (П.6)
. (П.6)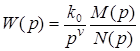 ).
).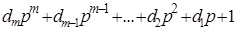 .
.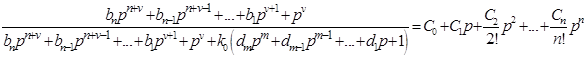 . (П.7)
. (П.7)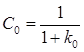 ,
, 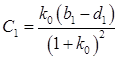 ,
, 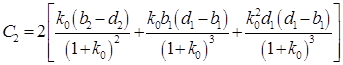 .
.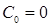 ,
, 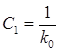 ,
, 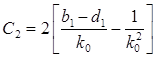 .
.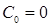 ,
, 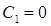 ,
, 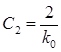 . (П.8)
. (П.8)