Пропорционально-интегрально-дифференциальный алгоритм регулирования (ПИД-алгоритм)
Этот алгоритм реализуется при помощи регулятора с передаточной функцией:
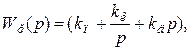 (2.9)
(2.9)
где 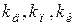 -постоянные коэффициенты.
-постоянные коэффициенты.
ПИД-закон регулирования, реализует алгоритм:
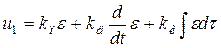 . (2.10)
. (2.10)
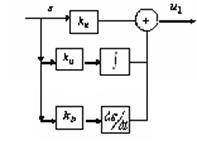 Совместное введение производной и интеграла обеспечивает желаемое быстродействие, необходимый запас устойчивости и отсутствие статической ошибки СУ. ПИД-алгоритм – наиболее гибкий алгоритм регулирования (в классе линейных алгоритмов). Он сочетает в себе преимущества более простых выше рассмотренных алгоритмов Коэффициенты
Совместное введение производной и интеграла обеспечивает желаемое быстродействие, необходимый запас устойчивости и отсутствие статической ошибки СУ. ПИД-алгоритм – наиболее гибкий алгоритм регулирования (в классе линейных алгоритмов). Он сочетает в себе преимущества более простых выше рассмотренных алгоритмов Коэффициенты 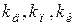 , входящие в передаточные функции типовых регуляторов, подлежат настройке при наладке СУ и поэтому называются настроечными параметрами. Они имеют наименования: - коэффициентыпропорциональной, интегральной и дифференциальной частей СУ.
, входящие в передаточные функции типовых регуляторов, подлежат настройке при наладке СУ и поэтому называются настроечными параметрами. Они имеют наименования: - коэффициентыпропорциональной, интегральной и дифференциальной частей СУ.
2.1.2 Методика выбора настроечных параметров 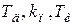 , при неизвестной модели ОУ экспериментальным методом
, при неизвестной модели ОУ экспериментальным методом
Алгоритм выбора настроечных параметров:
1. Отключить дифференциальный и интегральный каналы контроллера. Задать малое значение 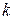 .
.
2. Получить переходной процесс на выходе, изменив значение задания для контролируемой переменной. Переходной процесс должен быть медленным.
3. Увеличить 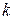 в два раза. Получить переходной процесс. Увеличивать
в два раза. Получить переходной процесс. Увеличивать 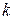 в два раза до тех пор, пока переходной процесс не станет колебательным.
в два раза до тех пор, пока переходной процесс не станет колебательным.
4. Увеличивать 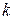 до тех пор, пока на выходе не будут получены непрерывные колебания. Запомнить полученные значения
до тех пор, пока на выходе не будут получены непрерывные колебания. Запомнить полученные значения 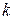 и периода колебаний
и периода колебаний 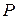 .
.
5. Выбрать параметры П, ПИ или ПИД контроллера по таблице 1.
Таблица 2.1 - Настроечные параметры 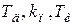 ,
,
| Контроллер | 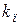 | 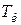 | 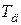 |
| П | 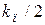 | - | - |
| ПИ | 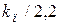 | 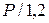 | - |
| ПИД | 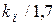 | 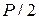 | 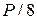 |
Режим непрерывных колебаний на выходе нежелателен для многих промышленных объектов. Поэтому можно увеличивать 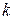 лишь до возникновения колебательного переходного процесса.
лишь до возникновения колебательного переходного процесса.
Пример -1. Для СУ приведенной на рисунке 2.2 (параметры К 1,2=1; Т1,2 =5),, реализовать пропорционально-интегрально-дифференциальный алгоритм регулирования и выбрать коэффициенты 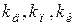 . Для этого воспользуемся ПК МВТУ /5/.
. Для этого воспользуемся ПК МВТУ /5/.

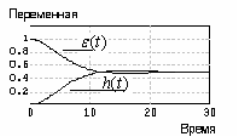
Рисунок 2.2 – Структурная схема СУ и графики переходного процесса и
установившейся ошибки
По графику 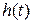 , определяем время регулирования
, определяем время регулирования 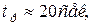 а по графику
а по графику 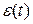 -ошибку
-ошибку 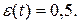
1. Реализуем модель ПИД- регулятора. Отключим дифференциальный и интегральный каналы контроллера, для чего весовые множители сумматора по этим каналам положим равным нулю. Зададим малое значение 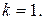 Увеличиваем
Увеличиваем 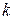 до тех пор, пока на выходе не будут получены непрерывные колебания. На рисунке 2.3, представлена схема СУ с ПИД-регулятором и графики
до тех пор, пока на выходе не будут получены непрерывные колебания. На рисунке 2.3, представлена схема СУ с ПИД-регулятором и графики 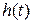 , для
, для 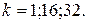
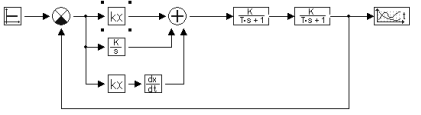
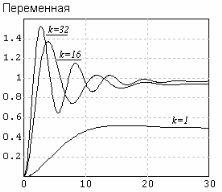 Рисунок 2.3 – Структурная схема СУ с ПИД регулятором и графики
Рисунок 2.3 – Структурная схема СУ с ПИД регулятором и графики 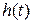 .
.
Полученные значения: для 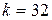 ; период колебаний
; период колебаний 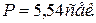 .
.
По эмпирическим формулам из таблицы 1, находим:
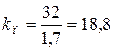 ;
; 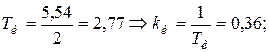
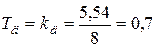 .
.
Установив полученные значения настроечных параметров в соответствующих блоках, и выполнив расчет, получим графики выходного процесса и ошибки (рисунок 2.4).
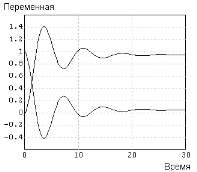 Рисунок 2.4 – Графики
Рисунок 2.4 – Графики 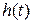 и
и 
По графику 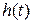 , определяем время регулирования
, определяем время регулирования 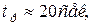 а по графику
а по графику 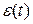 -ошибку
-ошибку 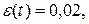 которая существенно уменьшилась по сравнению с исходной. Относительное перерегулирование
которая существенно уменьшилась по сравнению с исходной. Относительное перерегулирование 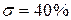 , что не соответствует требуемым показателям качества управления. Увеличение коэффициента
, что не соответствует требуемым показателям качества управления. Увеличение коэффициента 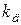 дифференциальной части регулятора приведет к уменьшению времени
дифференциальной части регулятора приведет к уменьшению времени 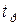 переходного процесса и уменьшению перерегулирования
переходного процесса и уменьшению перерегулирования 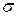 . На рисунке 2.5 представлены процессы, полученные при
. На рисунке 2.5 представлены процессы, полученные при 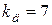 .
.
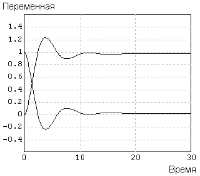 Рисунок 2.5 – Графики
Рисунок 2.5 – Графики 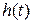 и
и  при
при 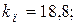
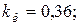
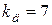 .
.
Обобщая результаты экспериментальных исследований можно сформулировать следующие общие выводы о влиянии настроечных параметров на показатели качества регулирования:
1.Увеличение коэффициента 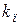 пропорциональной части регулятора приводит к увеличению перерегулирования
пропорциональной части регулятора приводит к увеличению перерегулирования 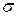 , времени
, времени 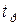 переходного процесса и уменьшению степени затухания .
переходного процесса и уменьшению степени затухания .
2.Увеличение коэффициента 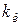 интегральной части регулятора приводит к увеличению времени
интегральной части регулятора приводит к увеличению времени 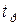 переходного процесса и увеличению перерегулирования.
переходного процесса и увеличению перерегулирования.
3.Увеличение коэффициента 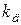 дифференциальной части регулятора приводит к уменьшению времени
дифференциальной части регулятора приводит к уменьшению времени 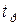 переходного процесса и уменьшению перерегулирования.
переходного процесса и уменьшению перерегулирования.
