Символьное (аналитическое) решение ОДУ

В Maxima представляется возможным с помощью специальные средств проводить аналитическое решение задачи Коши для систем обыкновенных дифференциальных уравнений, заданных как в явной форме dx/dt= F(t,x) , так и в неявной Mdy/dt=F(t,x), где М – матрица. Такие средства называют решателями ОДУ (solver ODE), обеспечивающих пользователю возможность выбора метода, задания начальных условий и др. Одним из таких средств является функция ode2, позволяющая решать в символьном виде обыкновенные дифференциальные уравнения первого и второго порядков.

Синтаксис вызова функции ode2

ode2(eqn, dvar, ivar),

где eqn - выражение, определяющее вид дифференциального уравнения;

dvar - зависимая переменная;

ivar - независимая переменная.

Посредством функции ode2 могут быть решены следующие типы ОДУ первого порядка: линейные, ОДУ с разделяющимися переменными, однородные ОДУ, уравнения в полных дифференциалах, уравнения Бернулли, обобщённые однородные уравнения.

Кроме того, при помощи функции ode2 могут быть решены следующие типы уравнений второго порядка: с постоянными коэффициентами; в полных дифференциалах; линейные однородные с переменными коэффициентами, которые могут быть сведены к уравнениям с постоянными коэффициентами; уравнения Эйлера; уравнения, разрешимые методом вариации постоянных; уравнения, свободные от независимой переменной, допускающие понижение порядка.

Тип используемого метода сохраняется в переменной method. При использовании интегрирующего множителя он сохраняется в переменной intfactor. Частное решение неоднородного уравнения сохраняется в переменной yp.

Для отыскания частных решений задач Коши с начальными условиями используются функции ic1(для уравнений первого порядка) и ic2 (для уравнений второго порядка).

Если ode2 не может получить решение, она возвращает значение false.

Рассмотрим примеры использования функции ode2.

Решить обыкновенное дифференциальное уравнение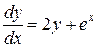

(%i1) ode2('diff(y,x)=2*y+exp(x), y, x);

(%o1) y=(%c - %e^(-x))*%e^(2*x)

система Maxima возвратила общее решение уравнение, где %c – постоянная интегрирования уравнения первого порядка.

Другой пример для уравнения второго порядка -

(%i5) ode2('diff(y,x,2)-3*'diff(y,x)+2*y=0, y, x);

(%o5) y=%k1*%e^(2*x)+%k2*%e^x

здесь %k1 и %k2 – постоянные интегрирования уравнения второго порядка. Для рассматриваемого уравнения второго порядка определим частное решение, удовлетворяющее начальным условиям при x = 0 y = 1, 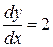(задача Коши).

(%i6) ic2(%,x=0,y=1,diff(y,x)=2);

(%o6) y=%e^(2*x)pflfx, риваемого уравнения второго порядка определим частное решение, удовлетворяющее начальным условиям

Дифференциальные уравнения первого порядка

Уравнение с разделяющимися переменными

Определяем частное решение

Однородное уравнение

Находим общее решение этого уравнения

Частное решение –

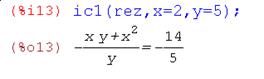
Линейное уравнение