Точечные и интервальные оценки. Доверительная вероятность и доверительный интеграл
Оценка, определяемая одним числом назыв. точечной.При выборке малого объема точечная оценка может существенно отличаться от истинного значения неизвестного параметра. В следствие этого пользуются интервальными оценками. Оценка, определяется двумя числами – концами интервалов назыв. интервальной.Пусть ά – оценка неизвестного параметра α, полученная по данным выборки. Очевидно, оценка тем точнее, чем меньше модуль разности α-ά.
Доверительной вероятностью или надежностью оценки параметра α назыв. вероятность γ с которой осущ. нерав-во: |α-ά|<δ, т.е. p(|α-ά|<δ)=γ (1.14)Обычно надежность γ задается заранее. В кач-ве γ берут число близкое к 1: 0,95; 0,99; 0,999… Ф-лу 1.14 можно записать в виде: р( 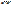 -δ<a<ά+δ)=γ.Эта ф-ла означает следующее: Р того, что интервал (
-δ<a<ά+δ)=γ.Эта ф-ла означает следующее: Р того, что интервал ( 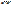 -δ; ά+δ) заключает в себе (покрывает) неизвестный параметр α и равна γ. Интервал, который покрывает неизвестный параметр α с заданной надежностью γ назыв. доверительным интервалом.Концы доверительного интервала назыв. доверительными границами.Доверит. границы явл. случайными величинами (они измен. от выборки к выборке). Доверит. интервал для оценки мат. ожидания а нормального распределения имеет вид:
-δ; ά+δ) заключает в себе (покрывает) неизвестный параметр α и равна γ. Интервал, который покрывает неизвестный параметр α с заданной надежностью γ назыв. доверительным интервалом.Концы доверительного интервала назыв. доверительными границами.Доверит. границы явл. случайными величинами (они измен. от выборки к выборке). Доверит. интервал для оценки мат. ожидания а нормального распределения имеет вид:
( 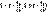 ,где δ0 – генеральное ср. квадрат. Откл-ие
,где δ0 – генеральное ср. квадрат. Откл-ие
 - выборочная средняя (1.15)
- выборочная средняя (1.15)
число t опр-ся равенством: 2𝜱(t)=γДоверит. интервал 1.15 показывает неизвестный параметр 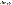 с надежностью γ. Если δ0 известно, то значение t берут с помощью таблиц ф-ии Лопласса. Если δ0 неизвестно и выборка мала, то вместо δ0 берут исправленное сред. квадрат. отклонение S.
с надежностью γ. Если δ0 известно, то значение t берут с помощью таблиц ф-ии Лопласса. Если δ0 неизвестно и выборка мала, то вместо δ0 берут исправленное сред. квадрат. отклонение S.
Доверительный интервал для оценки мат. ожидания нормального распределения.
Доверительной вероятностью или надежностью оценки параметра α назыв. вероятность γ с которой осущ. нерав-во: |α-ά|<δ, т.е. p(|α-ά|<δ)=γ (1.14)Обычно надежность γ задается заранее. В кач-ве γ берут число близкое к 1: 0,95; 0,99; 0,999… Ф-лу 1.14 можно записать в виде: р( 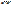 -δ<a<ά+δ)=γ.Эта ф-ла означает следующее: Р того, что интервал (
-δ<a<ά+δ)=γ.Эта ф-ла означает следующее: Р того, что интервал ( 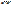 -δ; ά+δ) заключает в себе (покрывает) неизвестный параметр α и равна γ. Интервал, который покрывает неизвестный параметр α с заданной надежностью γ назыв. доверительным интервалом.Концы доверительного интервала назыв. доверительными границами.Доверит. границы явл. случайными величинами (они измен. от выборки к выборке). Доверит. интервал для оценки мат. ожидания а нормального распределения имеет вид:
-δ; ά+δ) заключает в себе (покрывает) неизвестный параметр α и равна γ. Интервал, который покрывает неизвестный параметр α с заданной надежностью γ назыв. доверительным интервалом.Концы доверительного интервала назыв. доверительными границами.Доверит. границы явл. случайными величинами (они измен. от выборки к выборке). Доверит. интервал для оценки мат. ожидания а нормального распределения имеет вид:
( 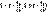 ,где δ0 – генеральное ср. квадрат. Откл-ие
,где δ0 – генеральное ср. квадрат. Откл-ие
 - выборочная средняя (1.15)
- выборочная средняя (1.15)
число t опр-ся равенством: 2𝜱(t)=γДоверит. интервал 1.15 показывает неизвестный параметр 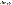 с надежностью γ. Если δ0 известно, то значение t берут с помощью таблиц ф-ии Лопласса. Если δ0 неизвестно и выборка мала, то вместо δ0 берут исправленное сред. квадрат. отклонение S.
с надежностью γ. Если δ0 известно, то значение t берут с помощью таблиц ф-ии Лопласса. Если δ0 неизвестно и выборка мала, то вместо δ0 берут исправленное сред. квадрат. отклонение S.
