Ограничения многочленной интерполяции

Многочленная интерполяционная функция очень чувствительна к выбору узлов интерполяции.

Рассмотрим интерполяционную формулу Лагранжа

,

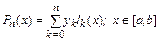где

.

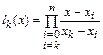Оценим норму функции 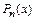, которую определим, как

.

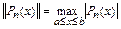С этой целью выполним очевидные преобразования:

.

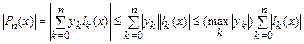Введем функцию Лебега:

.

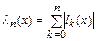Поскольку 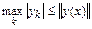, получаем оценку:

.

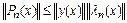Величина нормы функции 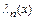зависит от распределения узлов интерполяции. Рассмотрим два случая.

Случай 1. Узлы интерполяции 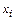на отрезке 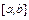распределены равномерно. В этом случае 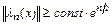(доказательство опускаем). При увеличении n многочлен 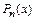может полностью оказаться непригодным для аппроксимации 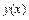, т. к. 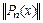неограниченно возрастает.

Рассмотрим такой пример. Будем интерполировать функцию

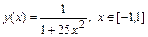
полиномом n-го порядка, выбирая узлы интерполяции равномерно распределенными. Введем норму ошибки интерполяции:

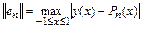
и исследуем ее зависимость от порядка интерполирующего полинома. Для этого обратимся к численным результатам (см. табл.8.1).

Таблица 8.1

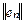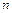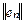	0.96		0.25		1.07
	0.71		0.30		2.10
	0.43		0.56		4.21

Видно, что с увеличением 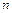погрешность интерполяции уменьшается вплоть до 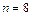. Дальнейшее увеличение порядка полинома приводит к возрастанию .

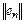Случай 2. Узлы интерполяции являются нулями полинома Чебышева. Их нетрудно получить, если на отрезке 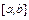построить полуокружность, разделить ее на 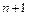равные части и спроектировать на отрезок середину каждой из них (рис. 8.1). В этом случае 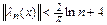(доказательство опускаем). Обратимся к рассмотренному выше примеру (см. табл.8.2) Погрешность интерполяции теперь при возрастании порядка полинома монотонно падает.

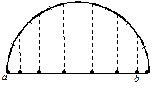
Рис. 8.1. Расположение нулей полинома Чебышева

Таблица 8.2

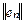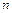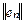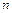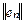	0.93		0.39		0.12
	0.75		0.27		0.08
	0.56		0.18		0.06

Многочленная интерполяция в точках Чебышева позволяет увеличивать точность приближения функции посредством увеличения порядка полинома. Однако привлекать узлы Чебышева не всегда удается. (Например, в узле Чебышева функция имеет особенность.) Чтобы избежать зависимости точности аппроксимации от локальных свойств функции, переходят к кусочно-полиномиальной аппроксимации.

Сплайн-интерполяция.

Назовем m-сплайнами полиномы невысокого порядка m, которыми аппроксимируется функция 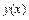на интервалах 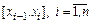и которые сшиваются в узлах интерполяции на основе требования непрерывности интерполирующей функции и ее первых 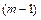производных.

Рассмотрим наиболее широко используемую на практике кубическую сплайн-интерполяцию. В ней искомая функция 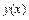на интервале 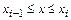аппроксимируется полиномом третьей степени

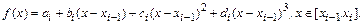(8.1)

Аналогичные полиномы можно записать для всех n интервалов, т. е. соотношение (8.1) справедливо для .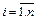

Условия сшивки сплайнов в узлах интерполяции:

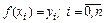, (8.2)

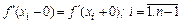, (8.3)

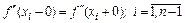. (8.4)

Кроме того, необходимо задать граничные условия в точках 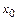и 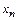. Это можно сделать несколькими способами. Здесь будем считать, что

,

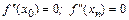т. е. будем рассматривать интерполяцию так называемыми естественными сплайнами.

Условие (8.2) приводит к уравнениям:

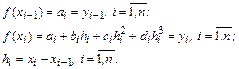(8.5)

Получили 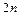уравнений относительно 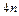неизвестных , .

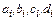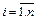Вычислим производные:

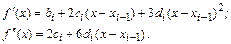
Построим уравнения, к которым приводит условие непрерывности первой производной в узлах 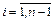. При кубической сплайн-интерполяции выражения для первой производной на соседних интервалах интерполирования имеют вид

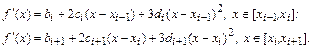
Требование непрерывности первой производной в узлах 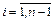(условие 8.3) приводит к уравнениям

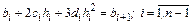. (8.6)

В свою очередь, непрерывность второй производной в этих же узлах (условие (8.4)) позволяет записать

,

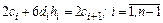или

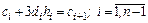. (8.7)

Наконец, из граничных условий 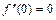, 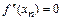получим, что

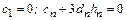. (8.8)

Соотношения (8.5), (8.6), (8.7), (8.8) составляют систему линейных алгебраических уравнений, всего 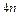уравнений, относительно 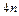неизвестных.

Построим эффективный метод решения этой системы. Выразим из (8.7) :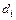

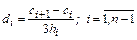, (8.9)

и подставим в (8.5):

.

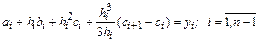Учтем, что :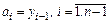

.

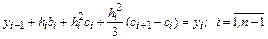Выразим из этого соотношения :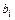

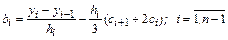. (8.10)

Подставим теперь 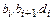в формулу (8.6):

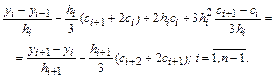
Выполним очевидные преобразования и запишем результирующую систему в виде:

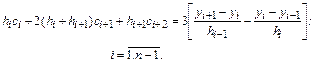(8.11)

Получили систему 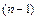линейных алгебраических уравнений относительно 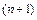неизвестных 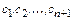. Однако, если учесть, что из граничных условий

,

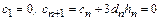то приходим к системе линейных алгебраических уравнений с треугольной симметрической матрицей

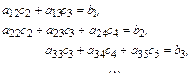
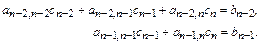
Обратите внимание: матрица системы обладает диагональным преобладанием! Эту систему можно эффективно решать методом 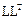-факторизации.

Вычислив коэффициенты 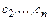, из соотношений (8.9) находим

.

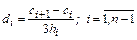Из условия (8.8) определяем :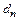

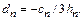
Коэффициенты 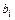рассчитаем из (8.10):

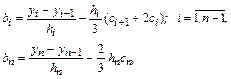
так как 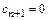. Коэффициенты 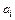, 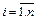известны из (8.5). В результате для всех 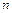кубических сплайнов определены коэффициенты .

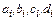Расчет значений функции 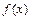методом сплайн-интерполяции осуществляется следующим образом:

1. По описанной выше методике вычисляются коэффициенты 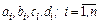кубических сплайнов;

2. Находится интервал 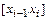, которому принадлежит данное 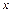. Значение функции 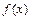на этом интервале вычисляется из кубического сплайна

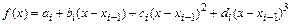
с параметрами 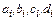для интервала .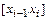