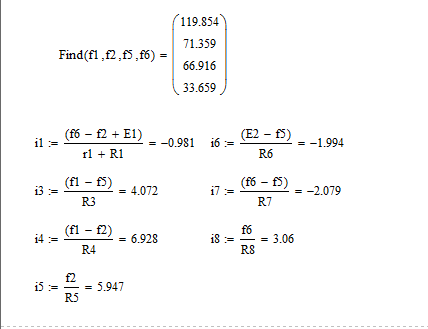Решение цепи постоянного тока методом узловых потенциалов
Электрическая цепь постоянного тока остается неизменной для данного метода.Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.
Теоретические основы
Если в цепи, состоящей из У узлов и Р рёбер, известны все характеристики звеньев (полные сопротивления R, величины источников ЭДС E и тока J), то возможно вычислить токи Ii во всех рёбрах и потенциалы φi во всех узлах. Поскольку электрический потенциал определён с точностью до произвольного постоянного слагаемого, то потенциал в одном из узлов (назовём его базовым узлом) можно принять равным нулю, а потенциалы в остальных узлах определять относительно базового узла. Таким образом, при расчёте цепи имеем У+Р–1 неизвестных переменных: У–1 узловых потенциалов и Р токов в рёбрах.
Не все из указанных переменных независимы. Например, исходя из закона Ома для участка цепи, токи в звеньях полностью определяются потенциалами в узлах:
Таким образом, минимальное число независимых переменных в уравнениях цепи равно либо числу звеньев, либо числу узлов минус 1, в зависимости от того, какое из этих чисел меньше.
При расчёте цепей чаще всего используются уравнения, записываемые, исходя из законов Кирхгофа. Система состоит из У–1 уравнений по 1-му закону Кирхгофа (для всех узлов, кроме базового) и К уравнений по 2-му закону Кирхгофа для каждого независимого контура. Независимыми переменными в уравнениях Кирхгофа являются токи звеньев. Поскольку согласно формуле Эйлера, для плоского графа число узлов, рёбер и независимых контуров связаны соотношением
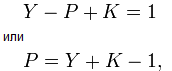то число уравнений Кирхгофа равно числу переменных, и система разрешима. Однако число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа уравнений является метод узловых потенциалов. Переменными в системе уравнений являются У–1 узловых потенциалов. Уравнения записываются для всех узлов, кроме базового. Уравнения для контуров в системе отсутствуют.
Расчет электрической цепи постоянного тока методом узловых потенциалов:
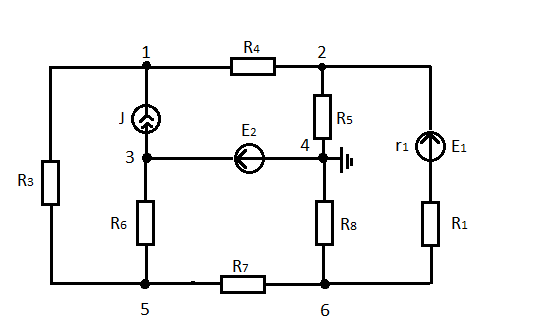
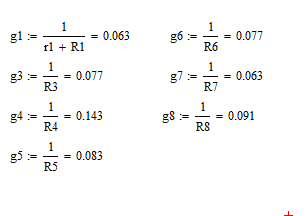Для проводимостей требуется разделить единицу на значения каждого резистора:
Исходя из алгоритма по решению данным методов запишем систему уравнений:
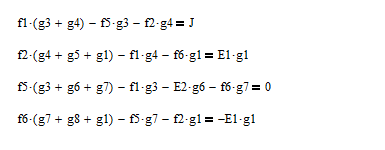
С помощью математического пакета MathCad14 решим СЛАУ и найдем токи, текущие в данной цепи на каждом резисторе:
