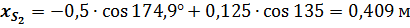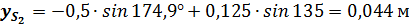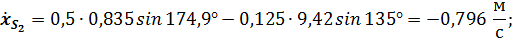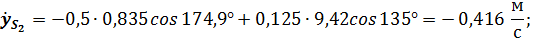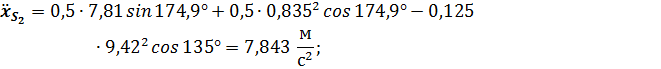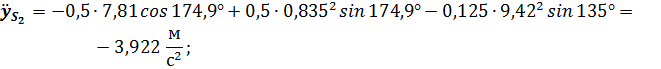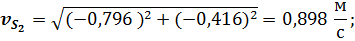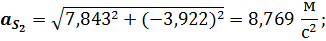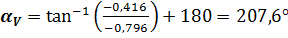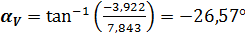Аналитический метод расчета
Кинематический анализ механизима
Структурный анализ КПМ по Ассуру позволяет представить механизм в виде совокупности первичного механизма (ведущее звено 1 и стойка) и двухповодковой группы (звенья 2 и 3). Кинематический и силовой анализ механизма проводят в соответствии с его структурным составом.
Кинематический анализ КПМ может быть выполнен либо аналитическим, либо графоаналитическим методом.
Аналитическим методом для одного расчетного положения механизма определяются положения, скорости и ускорения звеньев 2 и 3, а также точки S2.
Графоаналитическим методом для того же расчетного положения механизма определяются его кинематические параметры с помощью планов положений механизма , скоростей и ускорений
Аналитический метод расчета
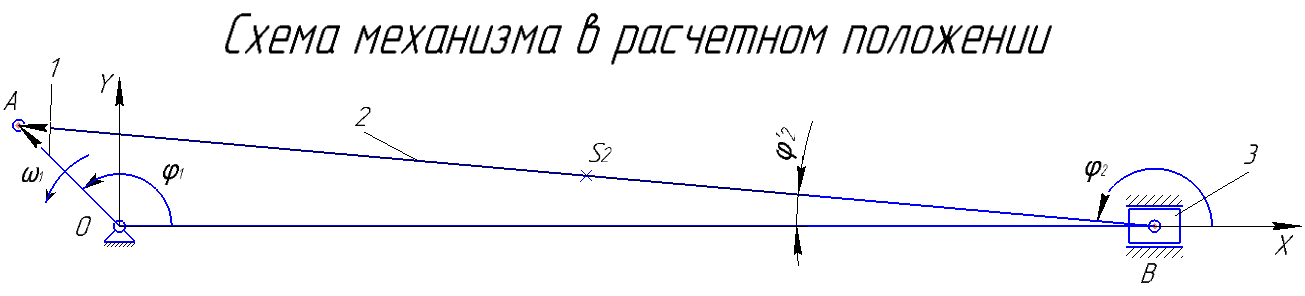
Рис. 2.1
Для решения задачи воспользуемся методом замкнутых векторных контуров. Для этого вдоль каждго звена, составляющего замкнутый контур, направляется вектор. Его угловое положение определяется углом, положительное направление которого отсчитывается в направлении против часовой стрелки от положительной полуоси абсцисс.
На рис.2.1 показаны направления векторов и соответствующие им углы для замкнутого векторного треугольника OBA.
Векторное уравнение замкнутого треугольника имеет вид
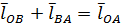
Спроектируем векторное уравнение на оси координат x и y :
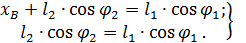
Из первого уравнения можно определить угол 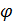 2 . Для принятых расчетных положений механизма он будет
2 . Для принятых расчетных положений механизма он будет
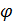 2 =
2 = 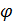 ’2 при xF = +1
’2 при xF = +1
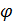 2 =
2 = 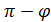 ’2 при xF = -1
’2 при xF = -1
где 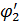 - острый угол, определяемый из треугольника OAB:
- острый угол, определяемый из треугольника OAB:
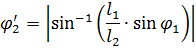
Из первого уравнения системы определяется координата точки B:
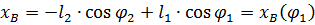
Для оперделения скоростей звеньев 2 и 3 продифференцируеи систму двух уравнений по времени
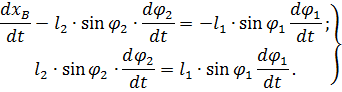
Или с учетом равенств
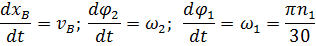
будем иметь систему
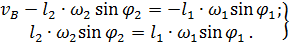
Из второго уравнения системы получим выражение для 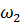 , а из первого – для
, а из первого – для 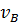 :
:
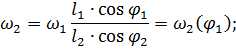
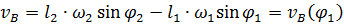
Повторное дифференцирование системы уравниений позволяет получить выражения для ускорений звеньев 2 и 3. С учетом равенств
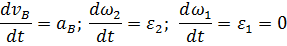
эти выражения имеют вид:
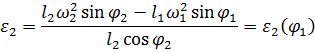
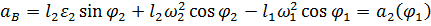
Численные значения кинематический параметров лдя расчетного положения заданного механизма будут следующими :
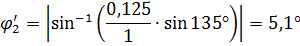
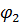 =
= 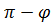 ’2 =
’2 = 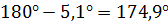
В радианной мере
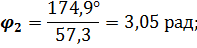
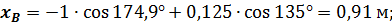
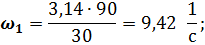
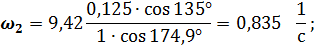
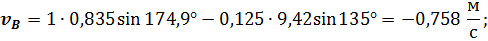
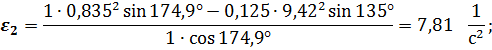
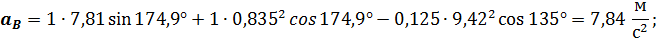
Для определения закона движения центра тяжести звена 2 – точки 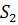 составляю новый замкнутый векторный контур
составляю новый замкнутый векторный контур 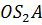 . Векторное уравнение его имеет вид:
. Векторное уравнение его имеет вид:
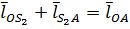
Проектируя уравнение на оси координат, получаю координаты точки 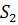
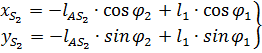
Первая и вторая производные от 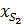 и
и 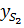 дадут значения составляющих скорости и ускорения точки
дадут значения составляющих скорости и ускорения точки 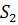 :
:
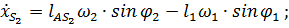
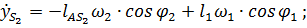
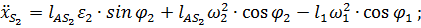
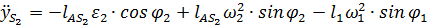 .
.
Значения полных векторов скорости и ускорения точки 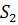 будут
будут
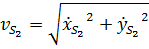
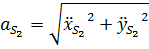
Положение векторов скорости отнсительно оси 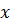 определяется углом
определяется углом 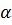
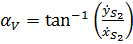 при
при 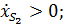
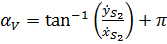 при
при 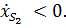
Аналогично определяется положение вектора ускорения:
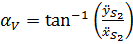 при
при 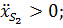
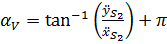 при
при 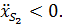
Подстановка в полученные выражения численных значений параметров заданного примера дает следующие результаты: