Структуры и алгоритмы функционирования стд

Оценку состояния ОД осуществляют различными методами, и классификация последних позволяет выбрать наиболее эффективный подход к их выбору. В результате такой классификации с учетом характера взаимодействия объекта и технических средств диагностирования можно выделить два метода - функциональное и тестовое диагностирование.

При методе функционального диагностирования объекта осуществляется наблюдение за функционированием ОД при воздействии на последний лишь рабочих воздействий и оценки его состояния по диагностическим признакам.

При методе тестового диагностирования на ОД осуществляют специальное воздействие, при этом ответная реакция объекта сравнивается с различными известными реакциями его состояния.

Таким образом, сравнивая эти методы, можно отметить, что метод функционального диагностирования аналогичен режиму пассивного эксперимента, а тестовое диагностирование - режиму активного эксперимента. Для решения задач оценки работоспособности, поиска дефектов, прогнозирования возможных изменений состояния ОД используются оба метода диагностирования.

Другой признак классификации — степень связи объекта и технических средств диагностики. По этому признаку различают методы, основанные на оценке выходных ОД или промежуточных показателей ОД. Методы оценки выхода объекта используются в основном при тестовом диагностировании и обеспечивают возможность установления работоспособности ОД, а также обнаружения возникших в нем дефектов. Использование метода оценки промежуточных показателей объекта предполагает необходимость введения в ОД специальных контрольных точек.

Остановимся на одном из способов оценки состояния ОД по методу оценки совокупности диагностических показателей (использование обобщенных показателей). Допустим, имеем вектор показателей 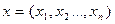и оценки вероятности попадания его в область работоспособности ОД. Такая задача имеет два решения: показатели его пространства могут попасть либо в пространство 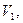либо в 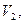соответствующие работоспособному и неработоспособному объектам.

Допустим, известна 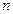- мерная плотность распределения вероятности 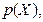тогда вероятность попадания случайного вектора X в область работоспособности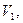

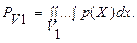(22.1)

Интеграл (22.1) может быть вычислен методом Монте-Карло с использованием ЭВМ.

При использовании вектора X для оценки нижнего (н) и верхнего (в) состояний работоспособности ОД область 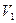находим из неравенства

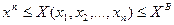
При оценке работоспособности ОД по отдельным показателям 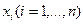область 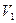находим из системы неравенств:

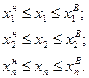
Принято считать, что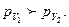

Известно, что по характеристикам можно судить о состоянии объекта, поэтому используются также методы оценки характеристик в целом или в отдельных точках. Здесь появляется еще один признак классификации состояния ОД - методы оценки по динамическим и статическим характеристикам. При этом оценка ОД по динамическим характеристикам может быть реализована по временным и частотным характеристикам.

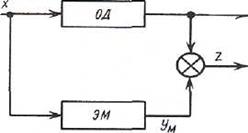
При функциональном алгоритме работы СТД осуществляется сравнение реакции объекта и эквивалентной модели (ЭМ) на одно и то же известное воздействие. Структура такой системы может быть представлена на рис. 22.1.

Как видно из схемы, входное воздействие 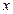поступает одновременно на ОД и ЭМ и выходные реакции объекта 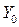и модели 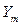сравниваются. Сигнал z на выходе сравнивающего устройства характеризует состояние объекта. При z=0 свойства ОД и ЭМ будут идентичны, т. е. объект работоспособен. Этот метод может быть также использован и при тестовом диагностировании.

Качество показателя при оценке состояния ОД в данном случае оценивается по критерию вида

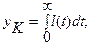
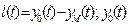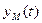где и -реакции соответственно объекта и модели.

При тестовом алгоритме диагностирования используемые методы различаются по характеру формирования тестового воздействия и способу обработки результатов реакции объекта. Рассмотрим один из методов, основанный на принципе неподвижной точки. Для ОД, как известно, справедлива зависимость 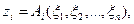где 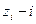-eзначение реакции объекта на произвольное входное воздействие; 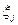значение его j -го показателя.

У₀

Рис. 22.1 Структура СТД с эквивалентной моделью:

ОД- объект диагностики,

ЭМ -эквивалентная модель

Следовательно, состояние ОД можно оценить, определив по реакциям 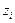прямые показатели 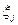и сравнив их с номинальными значениями.

Указанный принцип неподвижной точки предназначен для определения величин 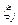Реакция объекта на входное воздействие описывается выражением 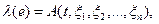зафиксировав 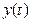в различные моменты времени, можно получить значение 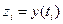и затем систему из п нелинейных уравнений:

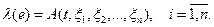
Умножив каждое из этих и нелинейных уравнений на произвольное вещественное число 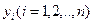и прибавив к ним соответствующее значение искомого показателя 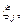получим систему, эквивалентную (22.2):

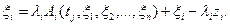
В результате решения системы (22.3) будут найдены координаты неподвижной точки 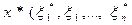в пространстве 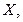если операций 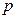преобразования этой системы представляет собой операцию сжатия.

Алгоритм диагностирования объекта по временным характеристикам имеет особую специфику. Использование этого алгоритма для определения работоспособности ОД или поиска дефекта может быть осуществлено различными способами в зависимости от заданного отклонения рабочей и эталонной характеристик. Например, такую оценку характеристики можно выполнить по числу точек (в пределе - максимальному) либо по некоторым показателям ее формы. В последнем случае оценки. Могут быть приведены, например, по числу и виду этих показателей.

Допустим, объект представляется на основе уравнения типа

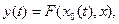
где x_o(t) - ступенчатое управляющее и возмущающее воздействие; х точка, принадлежащая n - мерному пространству показателей 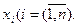Тогда алгоритм диагностирования можно реализовать путем сравнения действительного оператора 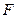с требуемым 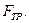Множество 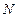возможных состояний, соответствующее различным значениям показателей 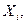в этом случае разбивается на' W + 1 подмножеств r, где W — число возможных дефектов в ОД.

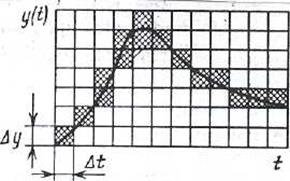Рис. 22.2 Зависимость y(t)

Совокупность S реализаций временной характеристики y(t), соответствующих точкам 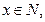и, будет равна величине W+1.Осуществляется сравнение характеристик, в результате чего устанавливается состояние ОД. Пример такого сравнения временной характеристики y(t) приведен на рис. 22.2. Здесь характеристика подвергается дискретизации по времени и уровню, а каждый прямоугольник 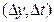рассматривается как некий информационный признак р изображения y(t). Шаг квантования по времени

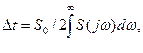(22.2)

где 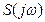— частотный спектр характеристики.

Справедливость для устойчивых по Ляпунову объектов выражения (22:2) обеспечивается при выполнении условия

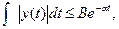
где В и а — положительные вещественные числа.

Значение шага квантования 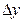определяется из требований к динамической точки ОД. Как правило, для большого числа следящих систем оно принимает значение

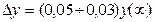
где 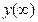— установившееся значение выходного сигнала ОД.

На рис. 22.3 показана реализация этого метода. От генератора стимулирующих сигналов ТСС на ОД поступает сигнал, 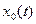и старт-импульс на синхронизатор С. Последний представляет собой временной распределитель и в моменты времени 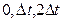обеспечивает подключение выходов блоков выделения большего БВБи меньшего БВМнапряжений. В каждый временной интервал 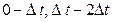t определяются максимальные и минимальные напряжения, т е. осуществляется дискретная оценка временных характеристик объекта диагностики. Далее осуществляется разделение множества реализаций y(t) на подмножества таким образом, чтобы каждое из них содержало в основном реализацию того образа, которому они объективно принадлежат. Затем на модели происходит формирование текущих значений характеристики ОД с учетом допусков напряжений сигналов.

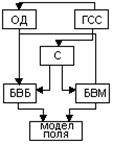
Рис. 22.3. Структурная схема реализации алгоритма диагностики

по временной характеристике:

ОД - объект диагностики; ГСС - генератор стимулирующих сигналов;

С — синхронизатор;

БВБ - блок выделения большого напряжения;

БВМ –блок выделения меньшего напряжения

Литература: осн. 3 [300-304]

Контрольные вопросы

1 Какие существуют методы исследования диагностических моделей?

2 Укажите основные методы диагностирования

3 Каковы основные алгоритмы функционирования СТД?

4 Структура СТД с эквивалентной моделью