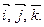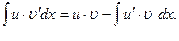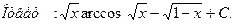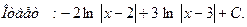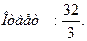Методические указания к решению первой
КОНТРОЛЬНОЙ РАБОТЫ
В этом параграфе приведён разбор решений задач типового варианта контрольной работы по математическому анализу.
ЗАДАЧА 1. Вычислить пределы функций а) —д):
а) 1. 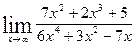 .
.
► 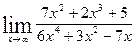 =
= 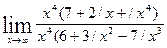 =
= 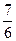 .
.
2. 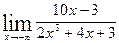 .
.
► 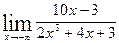 .=
.= 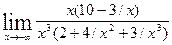 =
= 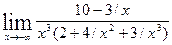 =
= 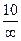 =0.◄
=0.◄
3. 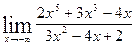 ..
..
► 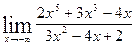 .=
.= 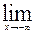
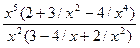 =
= 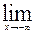
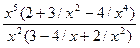 =
= 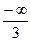 =-∞.
=-∞.
б) 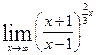 .
.
Решение. 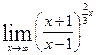 =
= 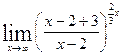 =
= 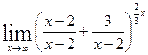 =
= 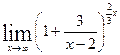 =
= 

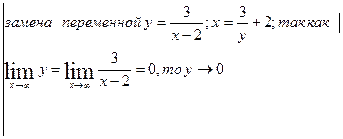 =
= 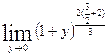 =
= 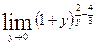 =
=
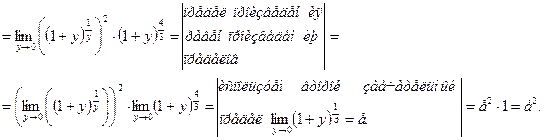
Предел 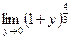 вычислен подстановкой
вычислен подстановкой 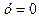
|
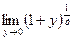 не может быть вычислен подстановкой
не может быть вычислен подстановкой 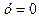 , поскольку в результате подстановки получается неопределенность
, поскольку в результате подстановки получается неопределенность 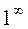 .
. в) 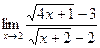 .
.
Анализ задачи.Подстановка числа 2 вместо 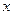 показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность
показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность 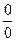 . Для этого можно либо провести тождественные преобразования выражения
. Для этого можно либо провести тождественные преобразования выражения 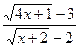 , либо применить правило Лопиталя.
, либо применить правило Лопиталя.
Решение.Выражение 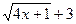 является сопряженным по отношению к выражению
является сопряженным по отношению к выражению 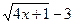 , а выражение
, а выражение 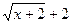 - по отношению к
- по отношению к 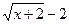 . Умножая числитель и знаменатель дроби на произведение сопряженных выражений (
. Умножая числитель и знаменатель дроби на произведение сопряженных выражений ( 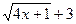 )·(
)·( 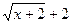 ), и используя формулу разности квадратов
), и используя формулу разности квадратов 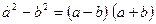 , получаем
, получаем 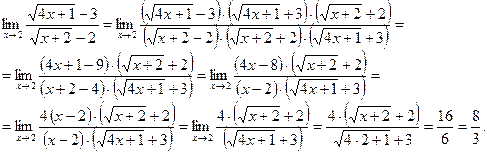
Другое решение задачи. Воспользуемся правилом Лопиталя
|
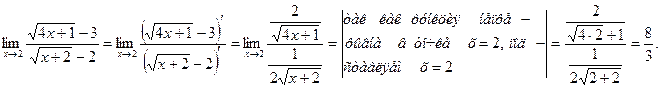
Анализ задачи.В данном случае, непосредственное применение теоремы о пределе частного невозможного, поскольку, как показывает подстановка числа. -3 вместо x и предел числителя и предел знаменатели равны пулю.
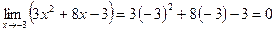 и
и 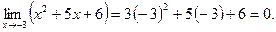
Таким образом, рассматриваемый предел представляет собой неопределённость вида 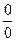 и для решения задачи требуется провести тождественные преобразования выражения, находящегося под знаком предела.
и для решения задачи требуется провести тождественные преобразования выражения, находящегося под знаком предела.
Решение.Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если 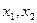 — корни квадратного трехчлена
— корни квадратного трехчлена 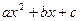 , то
, то 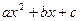 ,
,
= 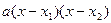 Решаем квадратное уравнение, находя его дискриминант D.
Решаем квадратное уравнение, находя его дискриминант D.
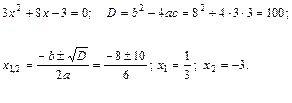
Отсюда,

Аналогично, 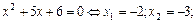
Поэтому, 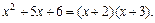
Преобразуем выражение находящиеся под знаком предела:
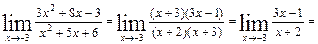 =
= 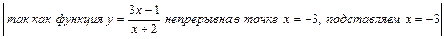 =
=
= 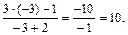
Другое решение задачи. Поскольку пределы числителя и знаменателя при 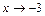
Равны нулю, применимо правило Лопиталя.
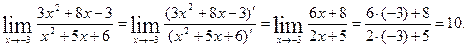
|
д) 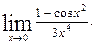
Анализ задачи. Подстановка числа 0 вместо x показывает, что пределы числителя и знаменателя при 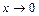 равны нулю. Поэтому, имеет место неопределённость
равны нулю. Поэтому, имеет место неопределённость 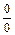 .
.
Для того, чтобы раскрыть неопределённость можно либо провести тождественные преобразования выражения, либо применить правило Лопиталя.
Решение. Совершим замену неизвестной 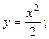 при этом
при этом 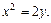
Так как 
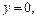 при
при 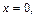 то
то 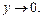
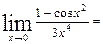
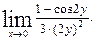
Используем теперь тригонометрическую формулу 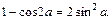
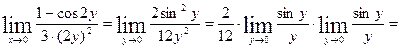
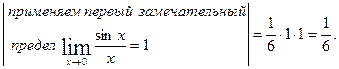
Другое решение. Воспользуемся вновь правилом Лопиталя
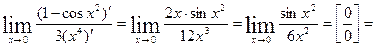
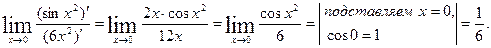
|
ЗАДАЧА 2.Вычислить производные функций а) – в):
а) Вычислить производную функции
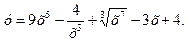
► 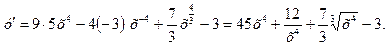 ◄
◄
б) Вычислить производную функции
1. 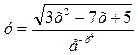 .
.
► 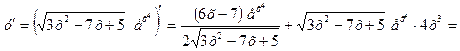
 ◄
◄
в) Вычислить производную функции
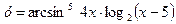 .
.
►  .◄
.◄
2. 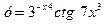 .
.
► 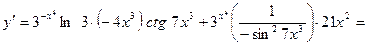
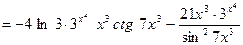 .◄
.◄
3. 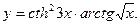
► 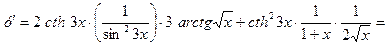
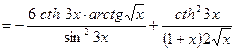 .◄
.◄
ЗАДАЧА 3.Исследовать функцию и построить график
Исследовать функцию 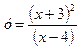 и построить её график.
и построить её график.
►Исследуем данную функцию.
1.Областью определения функции является множество 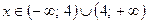 .
.
2.Ордината точки графика 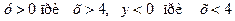 .
.
3.Точки пересечения графика данной функции с осями координат: 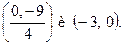
4.Легко находим, что 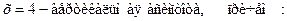
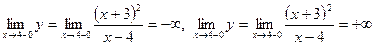 .
.
Находим наклонные асимптоты:
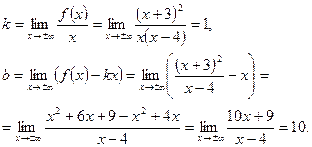
Таким образом, существует единственная наклонная асимптота 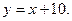
5. Исследуем функцию на возрастание, убывание, локальный экстремум:'
y= 2(х + 3)(x-4)-(x + 3)2 _ 2x2 – 2x - 24 – х2 - 6х - 9 =
(х-4)2 (x-4)2
= 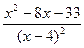 .
.
Из у' = 0 следует хг — 8х — 33 = 0, откуда 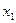 = 11, х2=— 3. В интервале (—∞; — 3) y'> 0, следовательно, функция возрастает в этом интервале; в (—3; 4) y'<0, т. е. функция убывает. Поэтому функция в точке х = —3 имеет локальный максимум: у( —3) = 0. В интервале (4; 11)
= 11, х2=— 3. В интервале (—∞; — 3) y'> 0, следовательно, функция возрастает в этом интервале; в (—3; 4) y'<0, т. е. функция убывает. Поэтому функция в точке х = —3 имеет локальный максимум: у( —3) = 0. В интервале (4; 11)
у' < 0, следовательно, функция убывает на этом интервале; в (11; +∞) у'>0, т. е. функции возрастает. В точке 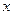 = 11 имеем локальный минимум: y(ll) =28.
= 11 имеем локальный минимум: y(ll) =28.
6. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем
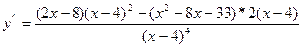 =
=
= 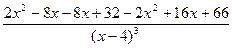 =
= 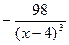 .
.
Очевидно, что в интервале (—∞; 4) y"< 0, и в этом интервале кривая выпукла; в (4; +∞)
у" > 0, т. е. в этом интервале кривая вогнута. Так как при х = 4 функция не определена, то точка перегиба отсутствует.
7. График функции изображен на рис. 0.17
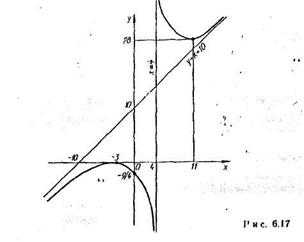
ЗАДАЧА 4.Вычислить неопределенные интегралы а) – в)
а)
1. 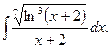
► 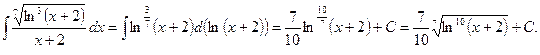 ◄
◄
2. 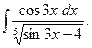
► 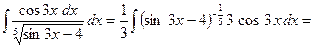
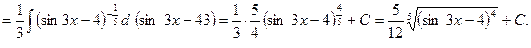 ◄
◄
3. 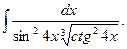
► 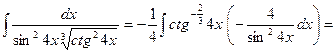
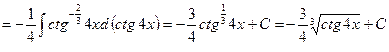 .◄
.◄
4. 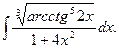
► 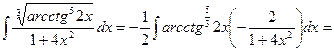
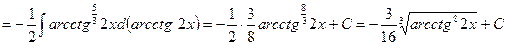 .◄
.◄
б) 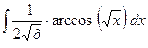 .
.
Решение. Решение данной задачи на формуле интегрирования по частям:
|
В этой формуле принимаем за
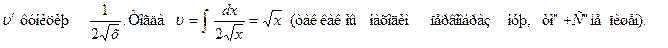 По формуле
По формуле 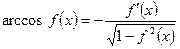 находим производственную второго сомножителя
находим производственную второго сомножителя 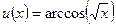 :
:
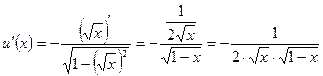
Подставляя найденные 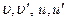 в формулу интегрирования по частям получаем:
в формулу интегрирования по частям получаем:
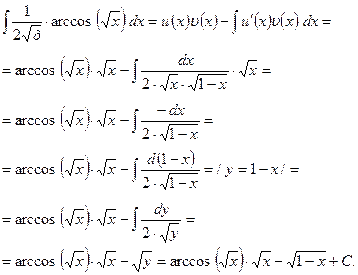
|
в) 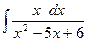 )
)
Решение.Так как корнями знаменателя является 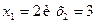 , то по формуле
, то по формуле 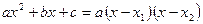 , знаменатель раскладываются на множители
, знаменатель раскладываются на множители
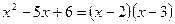 .
.
Подставим дробь в виде следующей суммы:
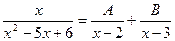 ,
,
и найдем коэффициенты А и В. Приведем дроби в правой равенства части к общему знаменателю:
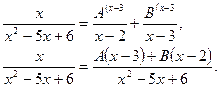
Приравняв числители, получим
(2) 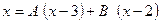 .
.
Подставив в последнее равенство  , находим, что
, находим, что
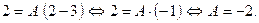
Подставляя 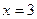 в равенство (2), находим, что
в равенство (2), находим, что
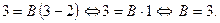
Таким образом, 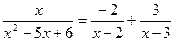 .
.
Итак, 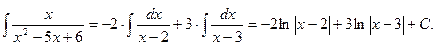
Здесь мы воспользуемся формулой (1)
|
ЗАДАЧА 5.Вычислите площадь фигуры, ограниченной графиками функций 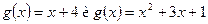 . Изобразите эту фигуру на координатной плоскости.
. Изобразите эту фигуру на координатной плоскости.
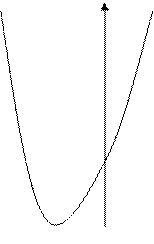
Решение. Графиком функции 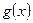 является парабола, ветви которой направлены вверх. Вычисляем производную функции
является парабола, ветви которой направлены вверх. Вычисляем производную функции 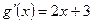 и находим координаты вершины параболы С:
и находим координаты вершины параболы С:
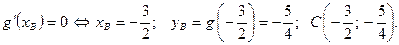
 |
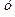
 |

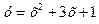
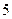
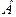
 |
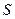
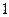
 |
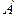
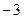
 |
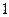
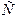 Рис. к задаче 5
Рис. к задаче 5
Найдем точки пересечения графиков функции : 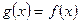 .
.
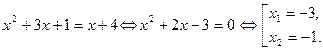
Заметим, что 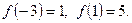 Графиком функции
Графиком функции 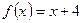 является прямая, которую можно построить по двум точкам
является прямая, которую можно построить по двум точкам 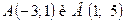 .
.
Пусть 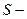 площадь фигуры
площадь фигуры 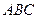 , ограниченной графиками функций. Так как
, ограниченной графиками функций. Так как 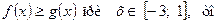
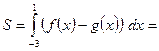
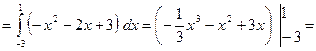
|
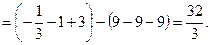
ЗАДАЧА 6.
Задание 1.
Даны координаты точек:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Координаты векторов 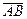 ,
, 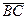 ,
, 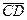 и
и 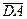 , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 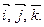
2. Координаты векторов 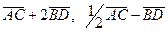 .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек (смотреть таблицу)
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
Решение.
Задание 1
Пусть даны точки A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
1. Для того чтобы найти координаты вектора, нужно из координат конца вычесть координаты его начала. Тогда 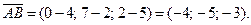 Аналогично находим координаты остальных векторов:
Аналогично находим координаты остальных векторов: 
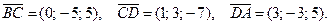
Найдём длины векторов:
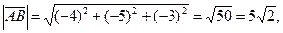
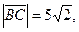
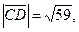
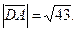
Запишем разложение этих векторов по базису 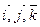 :
:
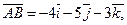
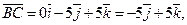

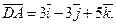
2. Используя правила действия с векторами, получаем:
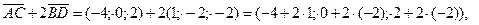
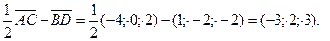
1. Внутренний угол ABC определяется как угол между векторами 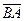 и
и 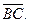 Предварительно найдём координаты этих векторов:
Предварительно найдём координаты этих векторов: 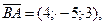
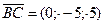 . Затем, используя формулы для вычисления скалярного произведения векторов и длины векторов, найдем косинус внутреннего угла ABC:
. Затем, используя формулы для вычисления скалярного произведения векторов и длины векторов, найдем косинус внутреннего угла ABC:

Задание 2.
Пусть даны точки A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
1. Треугольник ABC построен на векторах 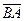 и
и 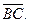 Для вычисления площади основания ABC найдём векторное произведение этих векторов:
Для вычисления площади основания ABC найдём векторное произведение этих векторов: 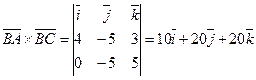 . Площадь треугольника ABC равна
. Площадь треугольника ABC равна 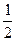 модуля векторного произведения:
модуля векторного произведения: 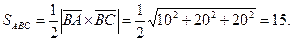
2. Пирамида ABCD построена на векторах 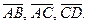 Объём пирамиды ABCD вычисляется как
Объём пирамиды ABCD вычисляется как 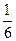 модуля смешанного произведения этих векторов:
модуля смешанного произведения этих векторов: 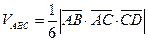 . Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то
. Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то 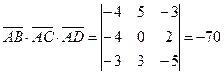 . Тогда
. Тогда 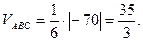
3. Длину высоты пирамиды DO, опущенную из вершины D на основание ABC, определим как расстояние от точки D до плоскости ABC. Для этого составим общее уравнение плоскости ABC. Будем использовать уравнение плоскости, проходящей через три точки A, B и C:
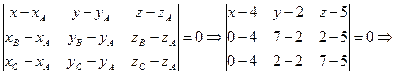 x+2y+2z-18=0.
x+2y+2z-18=0.
Используя формулу нахождения расстояния от точки до прямой, получаем:
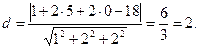
Итак, длина высоты DO равна 2.
Задание 3.
Пусть даны точки A(1; 3; 0), B(4; -1; 2), C(3; 0; 1), D(1; 2; 3).
1. Воспользуемся уравнением плоскости, проходящей через три точки A, B и C:
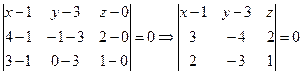 .
.
Раскрывая определитель и преобразуя полученное уравнение, получим общее уравнение плоскости ABC: 2x+y-z-5=0.
2. Для составления канонических и параметрических уравнений прямой AD, нам понадобится точка, лежащая на этой прямой (можно взять точку A или D), и направляющий вектор этой прямой. В качестве направляющего вектора прямой AD можно взять вектор 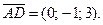 Тогда канонические уравнения прямой AD принимают вид:
Тогда канонические уравнения прямой AD принимают вид:
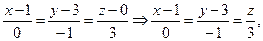
параметрические:
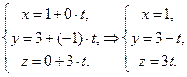
ЗАДАЧА 7.
Решить систему алгебраических линейных уравнений по правилу Крамера, матричным способом и методом Гаусса.
Пример. Рассмотрим систему алгебраических линейных уравнений:
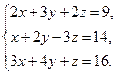
Решение.
1. Правило Крамера (см.[2] глава 10. стр.268).
Согласно этому правилу, 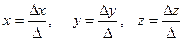 , где
, где
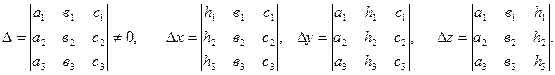
Находим определитель системы:
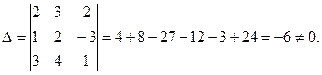
Следовательно, система является определённой. Для нахождения её решения вычисляем определители:
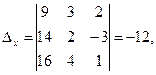
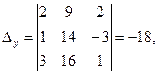
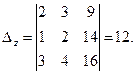
По формулам Крамера находим:
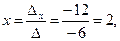
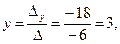
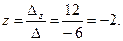
2. Матричный способ.
Введём обозначения: 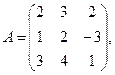
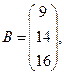
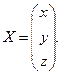 Тогда систему можно переписать в виде матричного уравнения:
Тогда систему можно переписать в виде матричного уравнения: 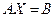 , решение которого находим по формуле
, решение которого находим по формуле 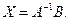 Прежде всего найдём матрицу
Прежде всего найдём матрицу 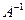 , обратную матрице
, обратную матрице 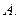 Определитель системы
Определитель системы 
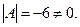 Следовательно для матрицы
Следовательно для матрицы 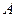 существует обратная. Вычислим алгебраические дополнения элементов этого определителя:
существует обратная. Вычислим алгебраические дополнения элементов этого определителя:
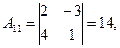
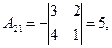
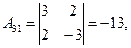
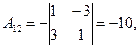
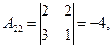
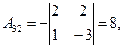
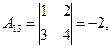
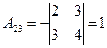
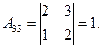
Отсюда 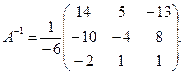
Тогда 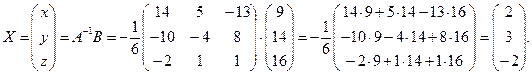
Итак, 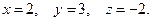
3. Метод Гаусса.
Метод Гаусса состоит в том, что с помощью элементарныхпреобразований система уравнении приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения, легко находят все неизвестные системы.
Составим расширенную матрицу и выполним над ней элементарные преобразования:
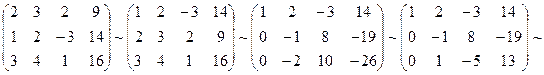

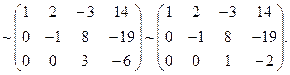
Здесь выполнены следующие преобразования:
а) первую и вторую строчки поменяли местами;
б) первую строчку умножили на -2 и сложили со второй, первую строчку умножили на -3 и сложили с третьей;
в) третью строчку разделили на -2;
г) вторую строчку сложили с третьей;
д) третью строчку разделили на 3.
Последней матрице соответствует следующая система уравнений:
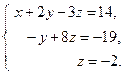
Из этой системы последовательно находим:
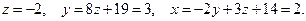
Контрольная работа № 1
Формулировки условий задач контрольной работы.
[1]. Вычислить предел функции.
[2]. Вычислить производную функцию.
[3]. Исследовать функцию, построить график.
[4]. Вычислить неопределённые интегралы.
[5] Вычислить площадь фигуры, ограниченной графиками функций f(x) и 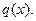
[6]. Найти общее решение дифференциального уравнения и построить графики двух
►Вариант 0◄
1. а) 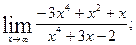 б)
б) 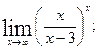
в) 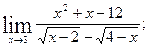 г)
г) 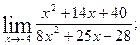
д) 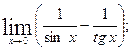
2. а) 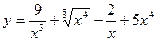 ; б)
; б) 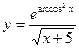 ;
;
в) 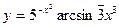
3. 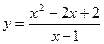 .
.
4. а) 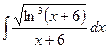 ; б)
; б)  ;
;
в) 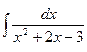 ;
;
5. 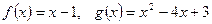 .
.
6. Задание 1.
Даны координаты точек:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Координаты векторов 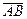 ,
, 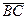 ,
, 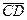 и
и 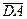 , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 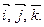
2. Координаты векторов 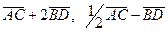 .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
Дано: 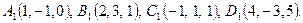
7.Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы
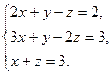
►Вариант 1◄
1. а) 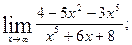 б)
б) 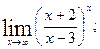
в) 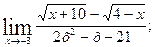 г)
г) 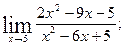
д) 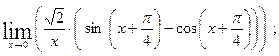
2. а) 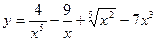 ; б)
; б) 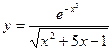 ;
;
в) 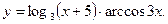
3. 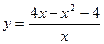 .
.
4. а) 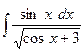 ; б)
; б) 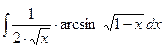 ;
;
в) 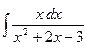 ;
;
5. 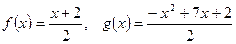 .
.
6. Задание 1.
Даны координаты точек:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Координаты векторов 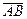 ,
, 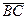 ,
, 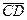 и
и 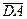 , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 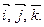
2. Координаты векторов 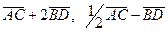 .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
1. Составить общее уравнение плоскости АВС.
2. Составить канонические и параметрические уравнения прямой АD.
Дано: 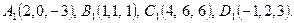
7.Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы
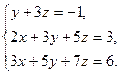
►Вариант 2◄
1. а) 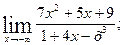 б)
б) 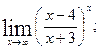
в) 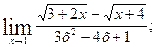 г)
г) 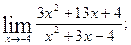
д) 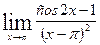 ;
;
2. а) 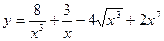 ; б)
; б) 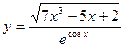 ;
;
в) 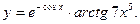
3. 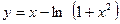 .
.
4. а) 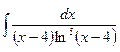 ; б)
; б) 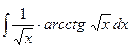 ;
;
в) 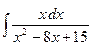 ;
;
5. 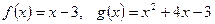 .
.
6. Задание 1.
Даны координаты точек:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Координаты векторов 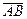 ,
, 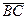 ,
, 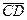 и
и 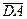 , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 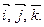
2. Координаты векторов 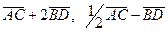 .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
Дано: 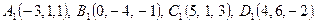
7.Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы
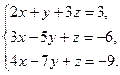
.
►Вариант 3◄
1. а) 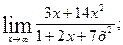 б)
б) 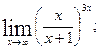
в) 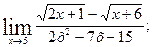 г)
г) 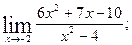
д) 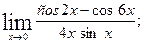
2. а) 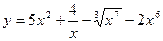 ; б)
; б) 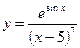 ;
;
в) 
3.  .
.
4. а) 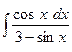 ; б)
; б) 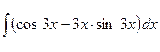 ;
;
в) 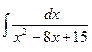 ;
;
5. 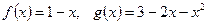 .
.
6. Задание 1.
Даны координаты точек:
А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3), D(х4, у4, z4).
Найти:
1. Координаты векторов 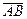 ,
, 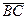 ,
, 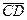 и
и 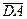 , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису