Практическое занятие №4
«Вычисление производной сложной функции. Производные и дифференциалы высших порядков»
Учебная цель:формировать умение находить производную сложной функции, производные и дифференциалы высших порядков.
Учебные задачи:
1.Научиться находить производную сложной функции.
2.Научиться находить производные и дифференциалы высших порядков.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- дифференцировать и интегрировать функции;
знать:
- основные понятия и методы математического анализа.
Задачи практического занятия №4
1.Повторить теоретический материал по теме практического занятия.
2.Ответить на вопросы для закрепления теоретического материала.
3.Решить задачи на нахождение производной сложной функции, производных и дифференциалов высших порядков.
4.Оформить отчет.
Обеспеченность занятия (средства обучения):
1. Справочная литература:
- Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И.Ермакова. – М.: ИНФРА-М, 2005. – 575 с.
- Таблица неопределенных интегралов.
2. Тетрадь для практического занятия.
3. Калькулятор.
4. Ручка.
Краткие теоретические и учебно-методические материалы
По теме практического занятия №4
Пусть y– сложная функция x, т.е. y= f(u), u = g(x), или
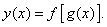
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u= g(x),то сложная функция также дифференцируема в точке xи находится по формуле
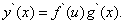
В случае сложной функции y = f(u),u = g(x) аргумент uфункцииyназывают промежуточным аргументом в отличие от независимой переменной x. Тогда правило дифференцирования сложной функции можно сформулировать так: производная сложной функции равна произведению производной этой функции по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x.
Вопросы для закрепления теоретического материала к практическому занятию №3:
1. Дайте определение сложной функции.
2. Сформулируйте правило нахождения производной сложной функции.
3. Дайте определение производной второго, третьего, n-го порядков.
4. Дайте определение дифференциала функции
Задания для практического занятия №3
Вариант №1.
Найти производную функции.
а) 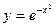 б)
б) 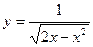 в)
в) 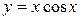
г) 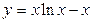 д)
д) 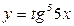 е)
е) 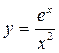
2.Найти производную второго порядка функции у = cos 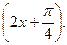
3.Найдите дифференциал третьего порядка 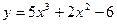
Вариант №2.
Найти производную функции
а) 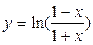 б)
б) 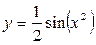 в)
в) 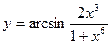
г) 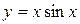 д)
д) 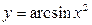 е)
е) 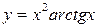
2.Найти производную второго порядка функцииу = tg 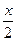
3.Найдите дифференциал третьего порядка 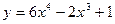
Вариант №3.
