Свойства пределов последовательностей

1. Последовательность, имеющая предел, ограничена.

2. Последовательность может иметь только один предел.

3. Любая неубывающая (невозрастающая) и ограниченная сверху (снизу) числовая последовательность имеет предел.

Рассмотрим числовую последовательность

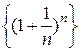. (6.1)

Эта последовательность возрастающая. Действительно, по формуле Бинома-Ньютона

,

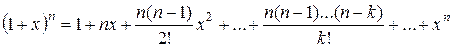Тогда имеем:

,

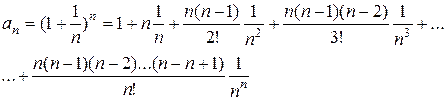или

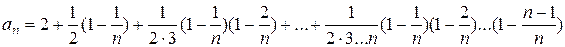. (6.2)

С увеличением 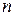каждое слагаемое, кроме первого, увеличивается и возрастает число слагаемых. Следовательно, 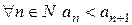, т.е. последовательность возрастающая.

Покажем, что последовательность (6.1) ограничена сверху. Заменим во всех членах разложения (6.2) выражения в скобках на 1; тогда

.

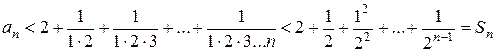Последняя сумма 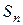, начиная со второго члена, представляет собой геометрическую прогрессию. Тогда

.

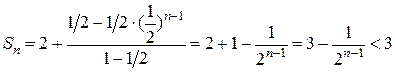Таким образом, показали, что последовательность (6.1) сверху ограничена числом 3, следовательно она имеет предел. Этот предел принято обозначать буквой :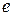

.

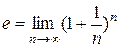Число 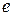является иррациональным, его приближённое значение 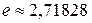. Число 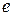принято за основание натуральных логарифмов. Для отыскания приближенных значений натуральных логарифмов по таблицам десятичных логарифмов пользуются формулой, полученной из формулы перехода к новому основанию:

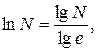где

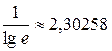
6.2

Число 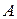называется пределом функции 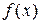при стремлении 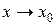, или в точке 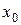, если для любого числа 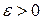существует такое числ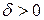о , что 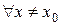, удовлетворяющих условию 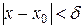, имеет место неравенство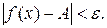

.

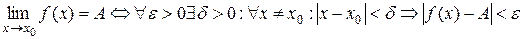Таким образом, число 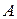есть предел функции 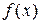в точке 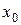, когда для всех 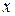достаточно близких к 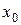и отличных от него, соответствующие им значения функции 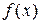оказывается сколь угодно близкими к числу .

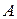Геометрически это означает, что для всех точек 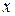, отстоящих от точки 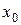, не далее чем на 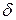, точки 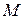графика функции 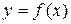лежат внутри полосы шириной 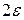, ограниченной прямыми .

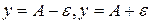Отметим, что 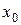- необязательно входит в область определения функции. Например: для функции 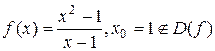, но предел функции в этой точка существует.

Характер стремления 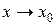может быть различным. Если 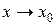, оставаясь меньше его, то говорят о левостороннем пределе функции, обозначают 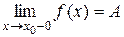. Если 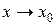, оставаясь больше его, то говорят о правостороннем пределе функции, обозначают .

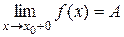Число 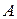- называется пределом функции при стремлении 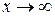, если 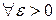существует такое положительное число 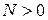, что для всех 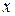удовлетворяющих условию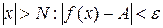

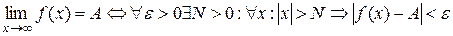
При вычислении пределов пользуются следующими теоремами:

Теорема 1. Предел постоянной равен самой постоянной: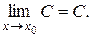

Теорема 2. Если функци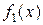и и 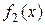имеют пределы в точке 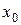, то в этой точке имеют пределы функции 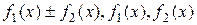, а если 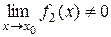, то имеет предел функция 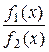, причем

,

,

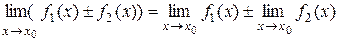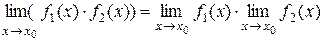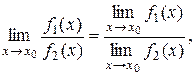если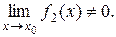

Следствие 1. Если существует 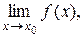то .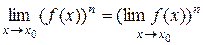

Следствие 2. .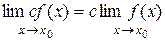

Замечание. Все сформулированные теоремы и следствия справедливы и при .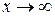

Пример 1. Вычислить предел функции .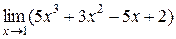

Решение. Для вычисления предела функции подставляем 1 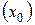вместо неизвестной, тогда 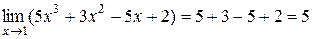. В этом примере предел функции в точке совпадает со значением функции в этой точке.

Покажем, как вычисляются пределы функции в точке, не входящей в область определения:

Пример 2. Найти предел функции .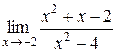

Решение. При подстановке 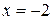, получаем и в числителе и в знаменателе дроби 0, т.е. имеем дело с неопределённостью вида 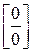. Для её раскрытия разложим числитель и знаменатель дроби на множители, после чего можно сократить выражения, которые давали нули и в числителе и в знаменателе:

.

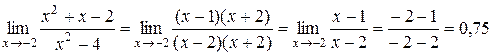Пример 3. Вычислить предел функции .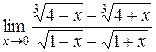

Решение. Вновь имеем дело с неопределённостью вида 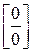. Однако, учитывая, что в числителе дроби содержаться радикалы, для избавления от неопределённости будем домножать на сопряжённые выражения числитель и знаменатель дроби:

.

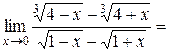
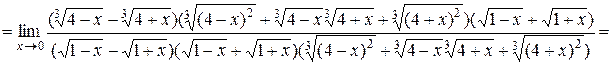
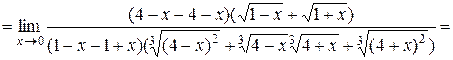
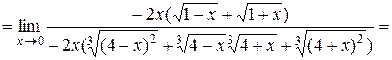
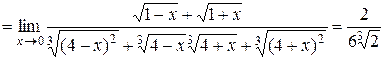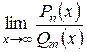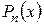При нахождении пределов вида , где и 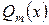- многочлены 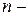ой и 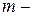ой степени, делим на старшую степень знаменателя. В результате выводим следующие правила:

· Если степень числителя больше степени знаменателя 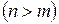, то .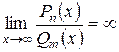

· Если степень числителя меньше степени знаменателя 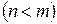, то .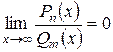

· Если степень числителя равна степени знаменателя 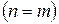, то 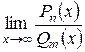равен отношению коэффициентов при старших степенях.

Пример 4. Вычислить .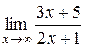

Решение. Так как степень числителя равна степени знаменателя, то предел равен отношению коэффициентов при старших степенях, т.е. .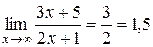

6.3

В некоторых случаях для раскрытия неопределённостей используют «замечательные пределы». Для их доказательства используются довольно тонкие рассуждения. Мы воспользуемся лишь готовыми результатами.

Предел вида 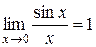носит название первого замечательного предела.

Первый замечательный предел используется для раскрытия неопределённости вида 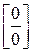при вычислении пределов от тригонометрических функций.

Получим следствия из первого замечательного предела.

· .

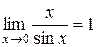Действительно, .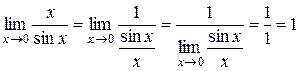

· .

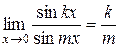Действительно, .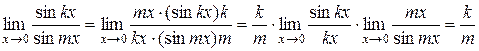

· .

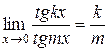Действительно, .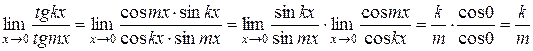

· .

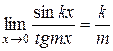Действительно, .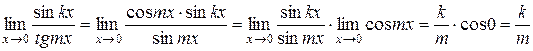

· .

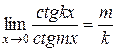Действительно, .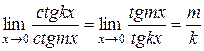

· .

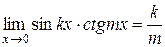Действительно, .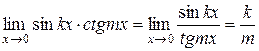

· .

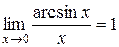Действительно, .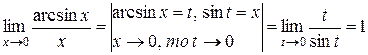

Предел, определяющий число 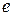, т.е предел вида 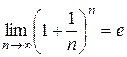, носит название второго замечательного предела. Другая форма второго замечательного предела может быть получена с помощью замены 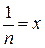. Тогда получаем 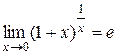. Заметим, что второй замечательный предел служит для раскрытия неопределенности вида .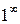