Разработка алгоритма решения задачи

КУРСОВАЯ РАБОТА

По дисциплине

«Программирование на языке высокого уровня»

Исполнитель: студент группы 4214

Дияров Д. Р.

Руководитель: Суздальцев И. В.

Оценка_________________

Подпись________________

“___” ________________2012 г.

КАЗАНЬ 2012

СОДЕРЖАНИЕ

1. Содержательная и формальная (математическая) постановка задачи
2. Разработка алгоритма решения задачи
3. Разработка структуры программы и алгоритмов программных модулей и их описание
4. Решение задачи на контрольном примере
5. Разработка и описание графа
6. Программная реализация алгоритма решения задачи и ее описание
7. Разработка системы тестов и отладка программы
7.1 Тесты черного ящика
7.2 Тесты белого ящика
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЯ. Листинг программы

Содержательная и формальная (математическая) постановка задачи

Проблема разбиения графов заключается в разбиении множества вершин графа на заданное количество подмножеств так, чтобы размеры этих подмножеств отличались не более чем на заданную величину и сумма весов рёбер, соединяющих эти подмножества – стоимость разбиения, была минимальна.

Разбиваются ориентированные графы с весами на вершинах и рёбрах. Размером подмножества вершин является сумма весов вершин входящих в это подмножество.

Исходными данными является граф G(X, U). Необходимо разбить множество X на два непустых и непересекающихся подмножества.Система обозначений математической модели для графа описан в табл. 1.

Таблица 1. Обозначение элементов.

№	Обозначение элементов математической модели	Наименование элементов математической модели	Примечание
	G(X,U)	Граф	неориентированный
	X	Множество вершин
	U	Множество ребер
	F	Критерий оптимизации число связей между X1 и X2

Рассмотрим математическое описание свойств исходных и результирующих данных. G(X, U), |X| = n. Условие деления на подмножества X₁ и X₂, X₁ÈX₂ =X, X₁ Ç X₂=Æ, X_i¹Æ .На формируемые узлы накладываются ограничения: |X₁| = n₁, |X₂| = n₂, n₁+n₂=n.

Математическое описание целевой функции выглядит следующим образом.

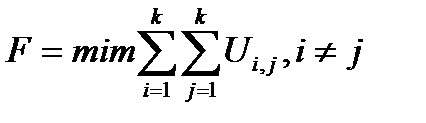(1)

Цель оптимизации минимизация критерия F.

Минимизация происходит при условии:

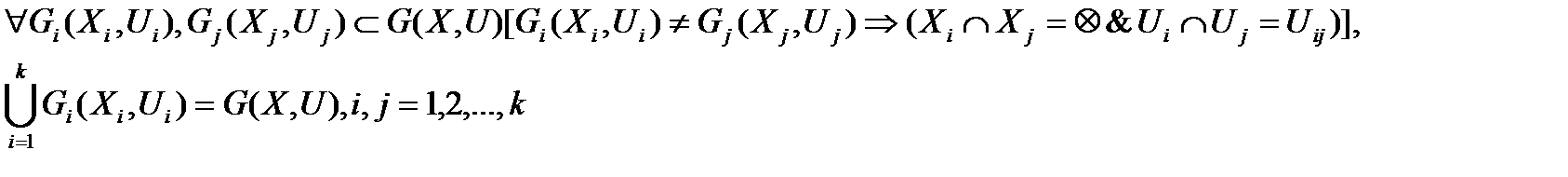(2)

Для любых двух подграфов G_i(X_i,U_i) и G_j(X_j,U_j) существует граф G_j(X_j,U_j), при том подграфы не должны быть равны, то есть пересечение подграфов G_i(X_i,U_i) и G_j(X_j,U_j) равно пустому множеству и пересечение ребер равно U_ij множеству ребер, соединяющих куски G_i(X_i,U_i) и G_j(X_j,U_j).

Задача разбиения графов практически необходима при разрезании СБИС схем, при распределении сетки метода конечных элементов на процессоры кластера, для решения задач аэродинамики и термодинамики, для переупорядочивания разреженных матриц с целью их быстрого параллельного умножения при параллельном решении систем уравнений и многих других практически важных областях. Скорость работы упомянутых параллельных методов существенно зависит от качества получаемых разбиений. Разрезанные рёбра разбиения представляют собой определённый объём коммуникации между процессорами. При снижении стоимости разбиения, сокращается объём передаваемых данных между процессорами, что приводит к увеличению производительности.[2].

Разработка алгоритма решения задачи

В последние годы интенсивно разрабатывается научное направление с названием «Природные вычисления», объединяющее математические методы, в которых заложены принципы природных механизмов принятия решений. Идея муравьиного алгоритма моделирование поведения муравьёв, связанного с их способностью быстро находить кратчайший путь от муравейника к источнику пищи. Основу поведения муравьиной колонии составляет самоорганизация, обеспечивающая достижения общих целей колонии на основе низкоуровневого взаимодействия благодаря которому, в целом, колония представляет собой разумную многоагентную систему. Особенностями являются наличие непрямого обмена, который и используется в муравьиных алгоритмах. Непрямой обмен – стигмержи, представляет собой разнесённое во времени взаимодействие, при котором одна особь изменяет некоторую область окружающей среды, а другие используют эту информацию позже, когда в неё попадают. Такое отложенное взаимодействие происходит через специальное химическое вещество – феромон (pheromone). Концентрация феромона на пути определяет предпочтительность движения по нему. При своём движении муравей метит путь феромоном, и эта информация используется другими муравьями для выбора пути. Концентрация феромонов определяет желание особи выбрать тот или иной путь. Однако, при таком подходе неизбежно попадание в локальный оптимум. Эта проблема решается благодаря испарению феромонов, которое является отрицательной обратной связью [3].

В работе используется представление задачи разбиения в виде адаптивной муравьиной системы, на основе сочетания принципов самообучения, самоорганизации и коллективной адаптации.

Система обозначений математической модели разбиения графа методом муравьиного алгоритма описана в табл. 2.

Таблица 2 Обозначение элементов.

№	Обозначение элементов математической модели	Наименование элементов математической модели	Примечание
	Pik	Вероятность включения вершины	случайное число от 0 до 1
	Q	Общее количество феромона	константа
	Dτk(l)	Количество феромона
	R(X, E)	Полный граф решений
	E	Множество всех ребер полного графа, связывающих множество вершин X
	Dk(l)	Число связей на графе G между множествами X1k и X2k,сформированными k-ым муравьем на l-ой итерации
	fik	Суммарный уровень феромона на ребрах графа R, связывающих xi с вершинами узла X1k(t)
	sik	Число связей на графе G между xi и X1k(t)
	ρ	коэффициент обновления
	α, β	управляющие параметры, которые подбираются экспериментально
	Fik	Потенциальная стоимость связей xi с Xсk(t)

На первом этапе каждой итерации каждый k-ый муравей формирует свое собственное множество X_1k. Процесс построения множество X_1k пошаговый. На каждом шаге агент применяет вероятностное правило выбора следующей вершины для включения ее формируемое множество X_1k(t).

Первый этап осуществляется следующим образом. Агент просматривает все свободные на данном шаге вершины X_сk(t). Для каждой вершины x_iÎ X_сk(t) рассчитываются два параметра:

По формуле (1) – при мультипликативной свертке, либо по формуле (2) – при аддитивной свертке определяется потенциальная стоимость F_ik связей x_i с X_сk(t).

F_ik=(f_ik)^α·(s_ik+1)^β (3)

F_ik=(f_ik)^α+(s_ik)^β (4)

Вероятность P_ik включения вершины x_iÎ X_сk(t) в формируемый узел X_1k(t) определяется следующим соотношением

P_ik=F_ik/ 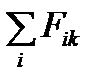(5)

Агент с вероятностью P_ik выбирает одну из вершин, которая включается в множество X_1k(t) и исключается из множества X_сk(t).

При α = 0 наиболее вероятен выбор вершины x_i максимально связанной с вершинами узла X_1k(t), то есть алгоритм становится жадным.

При β = 0 выбор происходит только на основании феромона, что приводит к субоптимальным решениям.

Поэтому необходим компромисс между этими величинами, который находится экспериментально.

После формирования за n₁ шагов муравьями узлов (каждый муравей – свой узел X_1k, на втором этапе итерации, каждый муравей откладывает феромон на рёбрах полного подграфа R_1кÌR, построенного на вершинах узла X_1k.

Количество феромона Dτ_k(l), откладываемое k-ым муравьем на каждом ребре подграфа R_1кÌ R, построенного на l-ой итерации, определяется следующим образом:

Dτ_k(l)= Q /D_k(l), (6)

После того, как каждый агент сформировал решение и отложил феромон, на третьем этапе происходит общее испарение феромона на ребрах полного графа R в соответствии с формулой (5) [3].

f_ik = f_ik(1- ρ), (7)

Рисунок 1 Блок-схема алгоритма.

Рисунок 1Продолжение.